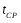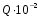Задача 4. Задача 4 4 Метод поэлементных проверок Теоретические сведения

• Название: Задача 4 4 Метод поэлементных проверок Теоретические сведения
• Дата: 13.03.2019
• Размер: 79.03 Kb.
• Имя файла: Задача 4.docx
• Тип: Задача; #70288

Задача 4

2.4 Метод поэлементных проверок
Теоретические сведения

Рассмотрим устройство релейной защиты, стоящее из N функциональных блоков (рис. 2.1):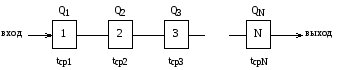


Рисунок 2.1 – Устройство релейной защиты
Пусть известно, что устройство отказало, но неизвестно, какой элемент отказал. Пусть также известны средние времена проверок элементов t_cpi и априорные (доопытные) вероятности отказов элементов Q_i.

Необходимо разработать алгоритм диагностики, оптимизировав его по критерию максимальной скорости получения информации.

Рассмотрим вначале ситуацию, когда средние времена проверок одинаковы.

t_cp1 = t_cp2 = t_cp3 = … =t_cpN. (2.1)
Сумма априорных вероятностей отказа равна единице: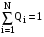
. (2.2)
Как следует из названия метода, в результате каждой элементарной проверки имеется возможность определить состояние только одного элемента. Таким образом, все устройство разбивается как бы на две части: проверяемый элемент и все остальные элементы. Выше уже рассматривалось зависимость энтропии системы от вероятностей отказов входящих в нее элементов. На рис. 2.2 показана такая зависимость для метода поэлементных проверок.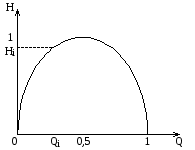


Рисунок 2.2 - Зависимость H(Q)
Для максимальной скорости получения информации при условии (2.2)

необходимо для первой проверки выбрать такой элемент, у которого априорная вероятность отказа ближе всего к 0,5. Вторая элементарная проверка должна проверять следующий элемент из оставшихся, вероятность отказа которого также ближе всех к 0,5. Практически же указанное условие будет соблюдаться, если алгоритм проверок имеет вид: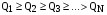
. (2.3)
Если средние времена проверок различны, то необходимо рассчитывать скорость получения информации при каждой элементарной проверке. Но, учитывая рис. 2.3, можно алгоритм представить в виде: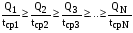
. (2.4)
Если априорные вероятности отказов элементов одинаковы:
Q₁ = Q₂ = Q₃ = … = Q_N, (2.5)
что может иметь место и при отсутствии достоверной информации о надежности функциональных блоков, а средние времена проверок различны, то получаем еще один алгоритм проверок:
t_cp1  t_cp2  t_cp3  …  t_cpN. (2.6)
Исходные данные:
Таблица 2.1 – Среднее время проверок

N опыта	1	2	3	4	5	6	7	8	9	10
	7 N	3 N	1 N	8 N	12N	15N	3 N	11N	10N	4 N

Таблица 2.2 – Вероятности отказов элементов системы

N опыта	1	2	3	4	5	6	7	8	9	10
N Варианта	2	3	4	5	6	7	8	9	10	11
1
1	0,05	0,23	0,14	0,04	0,07	0,1	0,11	0,18	0,05	0,03
2	0,1	0,24	0,01	0,09	0,14	0,21	0,05	0,07	0,03	0,06
3	0,13	0,11	0,26	0,02	0,05	0,14	0,23	0,02	0,01	0,03
4	0,20	0,06	0,09	0,10	0,01	0,15	0,03	0,01	0,24	0,11
5	0,16	0,18	0,03	0,08	0,07	0,05	0,11	0,26	0,04	0,02
6	0,01	0,24	0,05	0,09	0,07	0,16	0,19	0,07	0,10	0,02
7	0,23	0,03	0,04	0,06	0,11	0,13	0,18	0,06	0,06	0,10
8	0,24	0,02	0,05	0,10	0,27	0,01	0,08	0,11	0,02	0,10
9	0,04	0,06	0,19	0,07	0,07	0,17	0,29	0,02	0,01	0,08
10	0,11	0,08	0,14	0,03	0,06	0,08	0,13	0,12	0,15	0,10
11	0,20	0,11	0,03	0,05	0,07	0,18	0,15	0,13	0,02	0,06
12	0,14	0,23	0,08	0,09	0,05	0,06	0,17	0,02	0,10	0,06
13	0,01	0,06	0,09	0,05	0,25	0,17	0,03	0,05	0,09	0,20
14	0,12	0,14	0,01	0,05	0,08	0,14	0,03	0,10	0,30	0,03
15	0,04	0,06	0,18	0,10	0,06	0,05	0,19	0,02	0,25	0,05
16	0,05	0,07	0,09	0,18	0,19	0,05	0,04	0,03	0,10	0,20
1	2	3	4	5	6	7	8	9	10	11
17	0,05	0,19	0,11	0,01	0,03	0,04	0,16	0,04	0,31	0,08
18	0,04	0,02	0,13	0,13	0,07	0,03	0,17	0,05	0,08	0,28
19	0,26	0,04	0,10	0,10	0,01	0,07	0,04	0,10	0,19	0,09
20	0,03	0,06	0,16	0,02	0,16	0,15	0,02	0,10	0,15	0,15
21	0,04	0,03	0,07	0,19	0,14	0,20	0,01	0,02	0,19	0,11
22	0,02	0,09	0,14	0,06	0,08	0,11	0,17	0,01	0,07	0,25
23	0,05	0,06	0,16	0,13	0,07	0,04	0,02	0,18	0,09	0,20
24	0,04	0,02	0,19	0,13	0,04	0,02	0,08	0,04	0,34	0,10
25	0,11	0,19	0,01	0,01	0,03	0,19	0,07	0,05	0,05	0,29
26	0,17	0,03	0,02	0,05	0,06	0,02	0,07	0,06	0,22	0,30
27	0,02	0,04	0,08	0,06	0,04	0,19	0,17	0,15	0,18	0,07
28	0,10	0,16	0,01	0,02	0,04	0,05	0,10	0,05	0,12	0,35
29	0,09	0,06	0,05	0,11	0,13	0,05	0,06	0,18	0,01	0,26
30	0,09	0,17	0,16	0,02	0,04	0,05	0,06	0,17	0,08	0,16
31	0,05	0,03	0,05	0,13	0,13	0,16	0,01	0,05	0,15	0,24

Пример решения:
Таблица 2.9 – Исходные данные

N опыта	1	2	3	4	5	6	7	8	9	10
	6	7	13	16	2	7	4	14	18	13
	17	32	9	2	19	43	40	50	35	12

1) ,
;



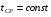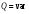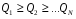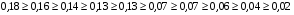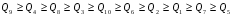2)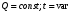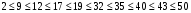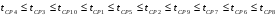


3)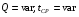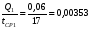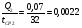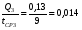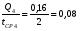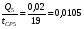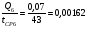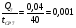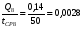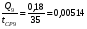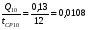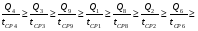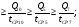
,
,
,
,
,





4) Найдем энтропию системы, для этого необходимо посчитать энтропию каждого из элементов системы: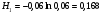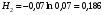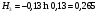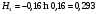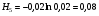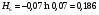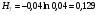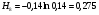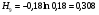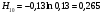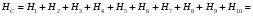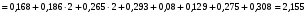