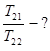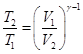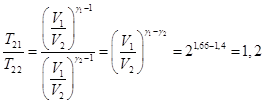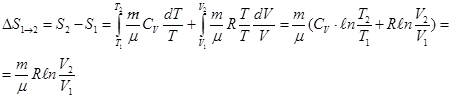4.14, 5.18, 5.23 5.28, 6.28, 6.52, 6.121, 5.81, 5.191,5.231
ЗАДАЧА №5.191
|
|
Два различных газа, из которых один одноатомный, а другой двухатомный, находятся при одинаковых температурах и занимают одинаковые объемы.
Газы сжимаются адиабатически так, что объем их уменьшается вдвое. Какой из газов нагреется больше и во сколько раз?
|
|
|
|
Дано:
i1 = 3
i2 = 5
Т’2 = Т’1
V’2 = V’1
S = const
V2 = 0,5 V1
| |
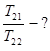
|
|
Решение:
Уравнение адиабаты в координатах V - T
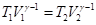
где γ – показатель адиабаты
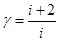
Перепишем первое равенство в виде
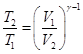
Отношение
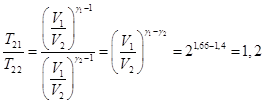
Ответ: одноатомный газ нагреется быстрее в 1,2 раза
ЗАДАЧА №5.231
|
Изменение энтропии на участке между двумя адиабатами в цикле Карно ΔS = 4,19 кДж/К. Разность температур между двумя изотермами ΔT = 100 К. Какое количество теплоты Q превращается в работу в этом цикле?
|
|
|
Дано:
ΔS = 4,19 кДж/К =4,19·103Дж/К
ΔT = 100 К
| |
А - ?
|
|
Решение:
Изменение энтропии идеального газа при изотермическом процессе
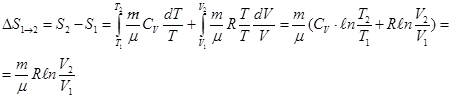
Работа цикла Карно
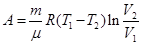
Количество теплоты Q, которое превращается в работу в этом цикле
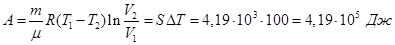
Ответ: 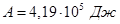
|
|
|
|
ЗАДАЧА №5.81
|
В сосуде объемом V = 2 л находится азот при давлении р = 0,1 МПа. Какое количество теплоты Q надо сообщить азоту, чтобы:
а) при p = const объем увеличился вдвое; б) при V = const давление увеличилось вдвое?
|
|
Дано:
V1 = 2 л =2·10-3 м3
р1 = 0,1 МПа = 0,1·106 Па
а) p = const
V2 = 2 V1
б) V = const
р2 = 2 р1
i =5
______________________________
| |
Q - ?
|
|
Решение:
а) p = const
Из уравнения Менделеева - Клапейрона
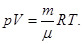
выразим температуру Т1 до нагревания
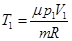
Из закона Гей-Люссака для изобарного процесса
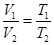
выразим температуру Т2 после нагревания
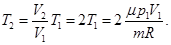
Количество теплоты Q, сообщенное газу 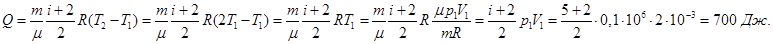
б) V = const
Из закона Шарля 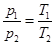
выразим температуру Т2 после нагревания
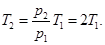
Количество теплоты Q, сообщенное газу 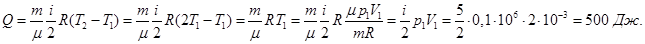
Ответ: а)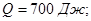 б) б) 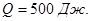
|
|
|
|
|
|
|
|
|
|
|
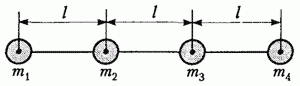
Задача 4.14
Решение:
|
|
|
Допустим мы отыскали такое место и подвесили за него систему из стержня и шаров. Явно что так как система неподвижна то в точке подвеса на стержень действует сила
|
|
|
|
А =(m1+m2+m3+m4)g=(1+5+7+3)*10=160Н
если система недвижна то сумма моментов сил условно любой оси одинакова нулю. нам нужно отыскать расстояние условно 3 шара, означает выберем любую ось так чтоб она проходила через центр шара 3 и точка подвеса условно нее на расстоянии х к примеру со стороны шаров 1 и 2
верховодило моментов
m1g*2L+m2g*L=m4g*L+(m1+m2+m3+m4)*g*x
x=L*(2m1+m2-m4)/(m1+m2+m3+m4)=0,2*(2*1+5-3)/(1+5+7+3) м = 0,05 м = 5 см
Ответ м=5см
Задача 6.121
По грунтовой дороге прошел трактор, оставив следы в виде ряда углублении, находящихся на расстоянии l = 30 см друг от друга. По этой дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на х0 = 2 см под действием груза массой m0 = 1 кг. С какой скоростью v катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски М = 10 кг.
Дано:
l = 30 см = 0,2 м
х0 = 2 см = 2·10-2 м
m0 = 1 кг
М = 10 кг
| |
v - ?
|
Коляска начнет сильно раскачиваться, если промежуток между двумя последовательными точками на углублениях будет равен периоду собственных колебаний коляски. Период собственных колебаний коляски находим из формулы
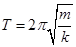
|
Решение:
Отсюда скорость коляски
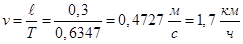
Ответ: 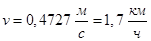
|
Масса, приходящаяся на каждую рессору
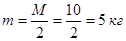
Коэффициент жесткости рессоры
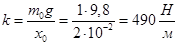
Следовательно,
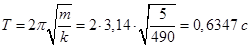
Время между двумя последовательными толчками
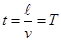




 |
 Скачать 2.12 Mb.
Скачать 2.12 Mb.