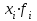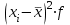статистика. Задача 5 Имеются данные по магазинам райпо за отчетный период (см табл ниже)
 Скачать 69.13 Kb. Скачать 69.13 Kb.
|
|
Задача 5 Имеются данные по магазинам райпо за отчетный период (см. табл. ниже). С целью изучения зависимости между средними товарными запасами на 100 рублей оборота розничной торговли и расстоянием магазинов до складов распределите магазины на три группы по расстоянию: до 10 км, от 10 до 50 км и свыше 50 км. В каждой группе и по итогу в целом подсчитайте: 1) количество магазинов; 2) объем оборота розничной торговли - всего; 3) сумму средних товарных запасов; 4) средние товарные запасы на 100 рублей оборота розничной торговли. Результаты группировки оформите в таблице. Сделайте выводы.
Решение: Построим ряд распределения магазинов: До 10 км. от 10 до 50 км. свыше 50 км. Составим групповую таблицу 2 Таблица 2
Вывод. Анализ интервального ряда распределения изучаемой совокупности магазинов по расстоянию до распределительных складов показывает, что наибольшее количество магазинов (12) имеют расстояние до распределительных складов от 10 до 50 км, а наименьшее количество магазинов (4) имеют расстояние до распределительных складов до 10 км. Распределение по расстоянию до распределительных складов имеет прямую связь с оборотами розничной торговли, т.е. с увеличением расстояния до распределительных складов увеличивается оборот розничной торговли на один магазин и обратную связь с средними товарными запасами, т.е. с увеличением расстояния до распределительных складов снижаются средние товарные запасыи на один магазин. Задача 12 Выпуск одноименной продукции и ее себестоимость по трем предприятиям за два периода:
Исчислите себестоимость единицы продукции в среднем по трем предприятиям за каждый период. Дайте обоснование применению формул средних для расчета показателей. Сделайте выводы. Решение: Себестоимость единицы продукции определяется по формуле: 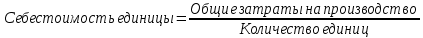 Для вычисления средней себестоимости одной машины в базисном году воспользуемся формулой средней арифметической взвешенной: Взвешенная средняя арифметическая — равна отношению суммы произведений значения признака к частоте повторения данного признака к сумме частот всех признаков. Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз. 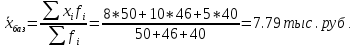 Вывод: Средняя себестоимость продукции в базисном году составила 7,79 тыс.руб. Для вычисления средней себестоимости одной машины в отчетном году воспользуемся формулой средней гармонической взвешенной: 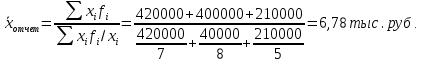 Средняя себестоимость продукции в отчетном году составила 6,78 тыс.руб. Задача 19 В результате 10 %-го выборочного обследования трудового стажа работников по предприятию получены данные:
Определите: средний стаж работы обследуемых работников (выборочную среднюю); дисперсию и среднее квадратическое отклонение стажа работы; коэффициент вариации; с вероятностью 0,954 пределы, в которых находится средний стаж работы всех работников предприятия. Сделайте выводы. Решение: Построим дополнительную таблицу 2 Таблица 2
Средний размер стажа определим по средней арифметической взвешенной 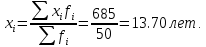 Мода – значение признака в вариационном ряду, встречающееся с наиб Дисперсия: 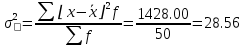 Среднеквадратическое отклонение 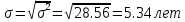 Коэффициент вприации: 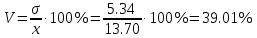 C вероятностью 0,954 пределы, в которых находится средний стаж работы всех работников предприятия. Найдем число работников : 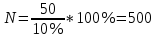 При уровне вероятности 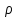 = 0,954 (t=2) = 0,954 (t=2)Доверительные интервалы будут находится : 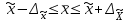 Средняя ошибка средней находим по формуле: 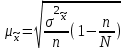 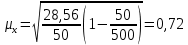 Δ = t * μ = 2*0,72=1,44 13,70-1,44 ˂ х ˂ 13,70+1,44 12,26 ˂ 15,14 Средний стаж работников составляет 13,70 лет., отклонение от среднего составляет 5,34 лет. Коэффициент вариации более 33%, следовательно, данная выборка неоднородна. С вероятностью 0,954 пределы, в которых находится средний стаж работы всех работников предприятия от 12,26 лет до 15.14 лет. Задача 26 Число вкладов населения в учреждениях Сберегательного банка России по региону на начало года представлено следующими данными:
Определить: вид динамического ряда; средний уровень динамического ряда; абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1 % прироста; средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда. Результаты расчетов представьте в таблице. Изобразите динамический ряд на графике. Сделайте выводы. Решение: Данный динамический ряд – моментный, так как характеризует состояние явления на определенные моменты времени. Средний уровень динамического ряда рассчитаем по формуле 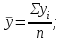 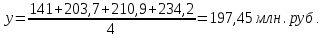 Абсолютный прирост (базисный и цепной)определим по формулам: Цепной: 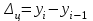 , ,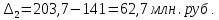 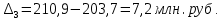 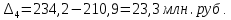 Базисный: 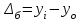 , ,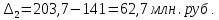 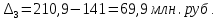 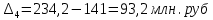 Базисный: Базисный: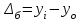 , ,Темп роста (базисный и цепной) определим по формулам: темп роста цепной: 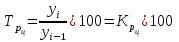 ; ;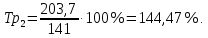 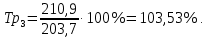 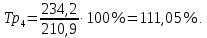 темп роста базисный: 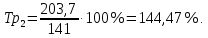 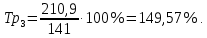 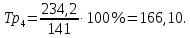 Темп прироста (базисный и цепной); цепной: 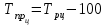 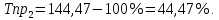 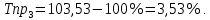 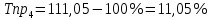 базисный: 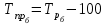 . .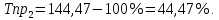 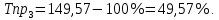 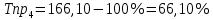 Средний абсолютный прирост определим по формуле: 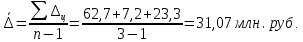 Средний темп роста определим по формуле 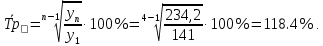 Cредний темп прироста определим по формуле: 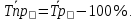 =118.4%-100% = 18.4% =118.4%-100% = 18.4%Изобразим динамический ряд на графике рис.1. 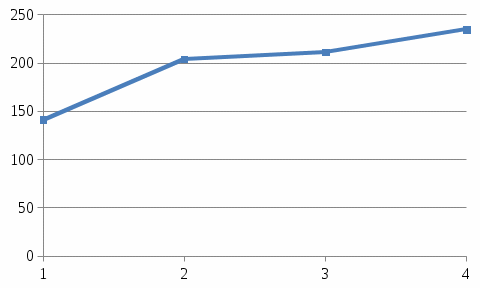 Рис.1. Динамика числа вкладов , млн.руб. Таким образом, за рассматриваемый период число вкладов ежегодно возрастало и в среднем составила 197,45 млн.руб., ежегодно в среднем число вкладов увеличивалось на 18,4% или на 31,07 млн.руб. Задача 33 По автотранспортному предприятию имеются следующие данные об объеме перевозок:
На основе приведенных данных требуется: выявить наличие сезонной неравномерности, используя графический метод; определить величину сезонной волны, используя индексы сезонности. Решение: Выявим наличие сезонной неравномерности, используя графический метод; 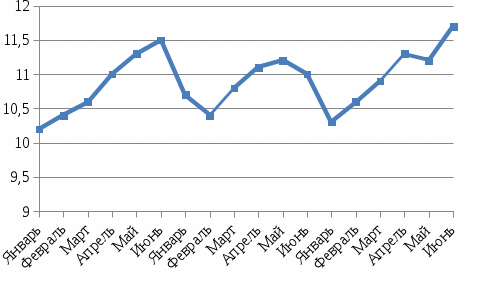 Рис.1. Объем перевозок Из рис.1. мы можем пронаблюдать , что в объеме перевозок имеется определенная сезонность. Индекс сезонности рассчитывается по формуле: 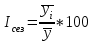 Для расчета индексов сезонности товарооборота составим вспомогательную таблицу:
То есть объем перевозок января составил в среднем 95,4% от объема за 6 месяцев, то есть был меньше чем за 6 месяцев на 4,6%. Объем перевозок февраля составил в среднем 96,0% от объема за 6 месяцев, то есть был меньше чем за 6 месяцев на 4,0%. Объем перевозок марта составил в среднем 98,8% от объема за 6 месяцев, то есть был меньше чем за 6 месяцев на 1,2%. Объем перевозок апреля составил в среднем 102,1 % от объема за 6 месяцев, то есть был больше чем за 6 месяцев на 2,1%. Объем перевозок мая составил в среднем 103,1% от объема за 6 месяцев, то есть был больше чем за 6 месяцев на 3,1%. Объем перевозок июня составил в среднем 104,6 % от объема за 6 месяцев, то есть был больше чем за 6 месяцев на 4,6%. Задача 40 Затраты предприятия на производство продукции за два периода:
Определите: 1) индивидуальный и общий индексы себестоимости; 2) общий индекс затрат на производство; 3) общий индекс физического объема производства; 4) абсолютную сумму изменения затрат – всего, в том числе за счет динамики себестоимости и количества произведенной продукции. Решение: 1. Индивидуальный индекс себестоимости продукции находится по формуле: iz=z1z0, где z1,0 – себестоимость отчетного и базисного периодов. Согласно условию задачи себестоимость единицы продукции А в отчетном периоде выросла на 20%, т.е. iz А=1+0,2=1,2 Аналогично по продукции Б и В: iz Б=1+0,12=1,12 iz В=1-0,02=0,980 Общий индекс себестоимости продукции равен: 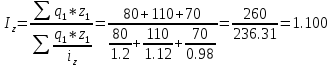 В целом по предприятию себестоимость единицы продукции выросла на 10%. Общий индекс затрат на производство определим как: 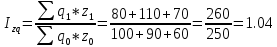 В целом по предприятию затраты на производство продукции выросла на 4%. Общий индекс физического объема производства 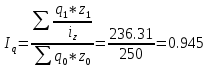 Общий индекс физического объема снизился на 5,5%. Абсолютная сумма изменения затрат – всего, 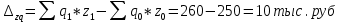 в том числе за счет динамики себестоимости 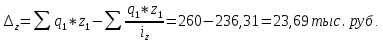 в том числе за счет количества произведенной продукции. 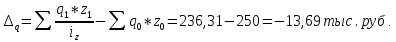 Задача 49 По данным задачи 7 для изучения тесноты связи между оборотом розничной торговли (результативный признак Y) и торговой площадью (факторный признак X) вычислите эмпирическое корреляционное отношение. Сделайте выводы.
Решение: Определим линейный коэффициент корреляции по формуле 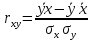 Составим дополнительную таблицу 2 Таблица 2
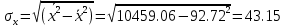 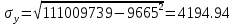 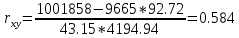 Коэффициент корреляции составил 0,584, тем самым мы видим умеренную связь между оборотом розничной торговли и торговой площадью. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||