Строймех. 8. Составная оболочка. Задание. Решение. Задача безмоментная теория и краевой эффект в составной оболочке
 Скачать 400.68 Kb. Скачать 400.68 Kb.
|
                 Задача: безмоментная теория и краевой эффект в составной оболочке Задача: безмоментная теория и краевой эффект в составной оболочке  Rв Rв Rв Rв R R        p p   H1   H Hx    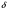 Исходные данные: 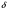 =2,5мм, толщина оболочки, R=0,5м, Н=1,5м, H1=2,0м, p =3атм избыточное давление (наддув), =2,5мм, толщина оболочки, R=0,5м, Н=1,5м, H1=2,0м, p =3атм избыточное давление (наддув), 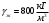 удельный вес жидкости. удельный вес жидкости.Определить: усилия и перемещения в верхнем полусферическом днище и части цилиндрической обечайки от наддува по безмоментной теории, усилия и перемещения нижнего полусферического днища и части цилиндрической обечайки от наддува и гидростатического давления по безмоментной теории, решить задачу краевого эффекта в зоне стыка верхнего днища и цилиндрической обечайки. Определение внутренних усилий в оболочке Верхнее полусферическое днище воспринимает только наддув. Меридиональное и окружное усилия определяются из двух уравнений равновесия – уравнения Лапласа (сумма проекций сил на нормаль к оболочке) и уравнения проекций сил на вертикальную ось: 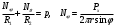 Здесь R1 и R2 – главные радиусы кривизны оболочки, r – радиус параллельного круга, Px – проекция равнодействующей внешней нагрузки на ось x, p – давление наддува. Здесь R1 и R2 – главные радиусы кривизны оболочки, r – радиус параллельного круга, Px – проекция равнодействующей внешней нагрузки на ось x, p – давление наддува.Верхняя часть цилиндрической обечайки также воспринимает только наддув. Меридиональное и окружное усилия определяются по приведённым в пункте 1 формулам. Нижняя часть цилиндрической обечайки воспринимает наддув и гидростатическое давление. Суммарное давление на оболочку определяется формулой 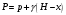 , , 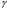 - удельный вес жидкости. - удельный вес жидкости.Внутренние усилия определяются по приведённым в пункте 1 формулам. Нижнее полусферическое днище воспринимает наддув и гидростатическое давление. Суммарное давление определить самостоятельно. Внутренние усилия определяются по тем же формулам. Пояснение к уравнению проекций сил на вертикальную ось оболочки Рисунок 1 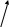   Px dp Px dp       ds ds         pd pd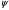  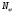 r r 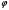 R R 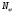 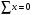 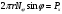 , отсюда , отсюда  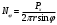 Определение Px 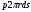 – элементарная сила, действующая на круговой элемент оболочки – элементарная сила, действующая на круговой элемент оболочки 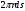 . Её проекция на ось x . Её проекция на ось x 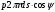 . . 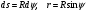  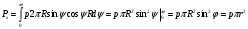 Тогда 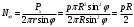 Полученная формула справедлива при p=const, если есть ещё гидростатическое давление (рис.3), переменное по высоте оболочки, то суммарное давление на стенки мы не можем вынести за знак интеграла. Необходимо интегрировать всё подынтегральное выражение.  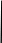        Рисунок 2 Px Рисунок 2 Px     Rв Rв Rв Rв  pR pR Nx Nx Для цилиндрической оболочки меридиональное усилие обозначим Nx. Рисунок помогает составить уравнение проекций сил на вертикальную ось и найти Nx. 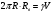 , где V – объём, занимаемый жидкостью, Rв – реакция подвески на вес жидкости, весом оболочки пренебрегаем. , где V – объём, занимаемый жидкостью, Rв – реакция подвески на вес жидкости, весом оболочки пренебрегаем.Рисунок 3          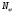 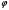 R R 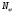  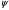 r r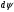 Px Здесь нормальная нагрузка на оболочку состоит из постоянного давления наддува и переменного гидростатического давления. Пользуясь этим рисунком, следует определить Px и 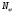 Определение перемещений Определение деформаций из физических соотношений 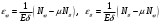 , , 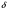 - толщина оболочки - толщина оболочкиДля сферических полуднищ меридиональное и нормальное перемещения определяются из формул: 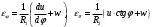 Для цилиндрической обечайки 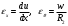 В результате интегрирования геометрических соотношений типа Коши, в решения для меридиональных перемещений войдут произвольные константы интегрирования, которые определяются из условий равенства меридиональных перемещений цилиндрической оболочки и полусферических днищ в зоне контакта, равенство нулю осевого перемещения цилиндрической оболочки в сечении закрепления, должно также выполняться условие равенства меридиональных усилий по линии стыка. Построение эпюр Построить эпюры перемещений и меридиональных усилий. Краевой эффект в зоне верхнего стыка двух оболочек Начало координат находится на пересечении линии стыка с осью оболочки Для цилиндрической оболочки уравнение краевого эффекта 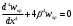 , , Где wкр часть прогиба, соответствующая краевому эффекту, 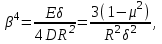 D – цилиндрическая жёсткость оболочки D – цилиндрическая жёсткость оболочки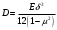 Решение уравнения  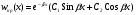 . Положительныеxнаправлены вниз. . Положительныеxнаправлены вниз. Суммарное перемещение 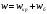 . Второе слагаемое соответствует безмоментному решению, положительные x от зоны стыка вниз. Решение, затухающее от зоны стыка вниз. C1 иC2 – произвольные константы интегрирования дифференциального уравнения краевого эффекта. . Второе слагаемое соответствует безмоментному решению, положительные x от зоны стыка вниз. Решение, затухающее от зоны стыка вниз. C1 иC2 – произвольные константы интегрирования дифференциального уравнения краевого эффекта. Для сферической оболочки 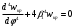 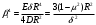 . . Решение уравнения 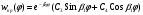 Положительная координата 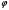 отсчитывается от зоны стыка вверх отсчитывается от зоны стыка вверхСуммарный прогиб оболочки 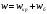 Определим через прогиб внутренние силовые факторы для цилиндрической оболочки 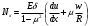 , , 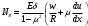 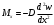 , , 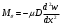 , , 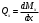 В формулах для меридионального и окружного усилий можно не учитывать составляющую прогиба от краевого эффекта ввиду незначительности вклада в решение по сравнению с безмоментным решением. Для сферической оболочки 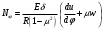 , , 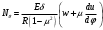 , , 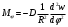 , , 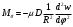 , , 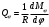 Произвольные константы определим из кинематических и статических условий сопряжения оболочек в зоне стыка при x=0 и 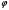 =0: =0: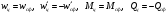 Построить эпюры прогиба по 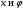 . .Замечание: для безмоментного решения и решения краевого эффекта имеем различные линии начала отсчёта. Это надо помнить. Но можно использовать единую исходную систему отсчёта, если перестроить решение краевого эффекта для прогиба, заменив x на (H1-x) для цилиндрической оболочки и φ на (π/2 -φ) для сферической оболочки. Составная оболочка. Решение по безмоментной теории. Верхнее полусферическое днище. R1=R2=R Меридиональное и окружное усилия определяем из двух уравнений равновесия – проекция всех сил на нормаль к поверхности оболочки и проекция всех сил на вертикальную ось для отсечённой части оболочки. 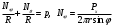 , ,где r – радиус параллельного круга, Px – проекция равнодействующей внешней нагрузки на вертикальную ось. 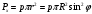 Результат 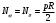 Определим деформации, пользуясь обобщённым законом Гука 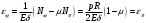 Меридиональное и окружное перемещения 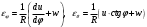 Выразив из второго wчерез окружную деформацию и меридиональное перемещение, получим 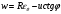 . .Исключим прогиб из первого равенства 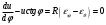 или 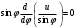 Интегрируя, получим 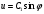 , где С1 – произвольная константа интегрирования, определяемая из условия равенства меридиональных перемещений полусферического днища и цилиндрической обечайки в зоне их стыка. , где С1 – произвольная константа интегрирования, определяемая из условия равенства меридиональных перемещений полусферического днища и цилиндрической обечайки в зоне их стыка. Цилиндрическая оболочка. 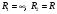 , , 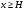 Из уравнения Лапласа 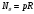 , ,из второго уравнения равновесия 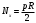 . .Деформации 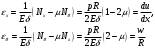 Отсюда получаем перемещения 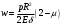 , u= , u=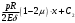 Константу С1 определим из условия контакта верхнего днища и цилиндрической обечайки Константу С1 определим из условия контакта верхнего днища и цилиндрической обечайки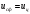 при при  для цилиндрической и для цилиндрической и  для сферической оболочек для сферической оболочекu=C1= 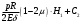 . Константу C2 определим из условия равенства нулю меридионального перемещения цилиндрической оболочки в месте закрепления, т.е. приx=H. Тогда . Константу C2 определим из условия равенства нулю меридионального перемещения цилиндрической оболочки в месте закрепления, т.е. приx=H. Тогда 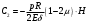 Решение: Для сферической оболочки 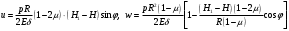 Для последующих расчётов определим угол поворота нормали к срединной поверхности оболочки по формуле: 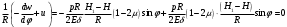 Для цилиндрической оболочки 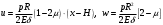 Если 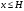 , то давление на стенки оболочки , то давление на стенки оболочки 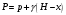 Тогда 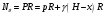 , , 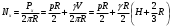 . . Определяем деформации из соотношений закона Гука 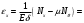 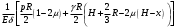 , ,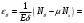 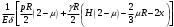 . .Перемещения определяем из соотношений Коши 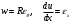 , ,Отсюда 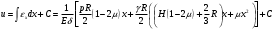 w= 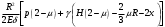 Нижнее полусферическое днище. R1=R2=R. 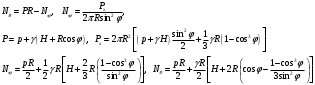 Деформации: 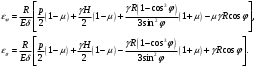 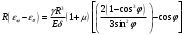 Определяем перемещения в нормальном и меридиональном направлениях 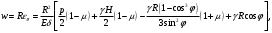  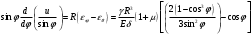 . .Из последнего равенства получим меридиональное перемещение 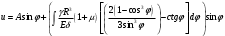 Или 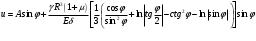 , ,Здесь А – произвольная константа интегрирования. Определение констант интегрирования С и A Меридиональное перемещение цилиндрической оболочки равно нулю в закреплении, отсюда 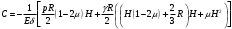 Из условия равенства меридиональных перемещений цилиндрической и сферической оболочки в зоне нижнего стыка, получим С=A Итак, меридиональное перемещение в цилиндрической оболочке 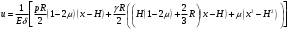 В сферической оболочке 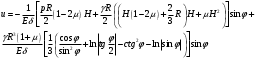 В зонах стыков условие равенства меридиональных усилий оболочек выполняется автоматически. Проверить.  Э «w»     Э «u»    0              На этом безмоментное решение завершается. Переходим к исследованию краевого эффекта в зоне стыка цилиндрической оболочки и верхнего полусферического днища. Начало координат переместим в сечение стыка днища и цилиндрической оболочки, в этом случае неудобство заключается в том, что для безмоментного решения мы имеем исходную систему координат, а для моментного состояния-другую систему. Чтобы сохранить исходную систему для обоих состояний, преобразуем решение краевого эффекта так, чтобы в зоне краевого эффекта показатель экспоненциальной функции обращался в ноль. Цилиндрическая оболочка 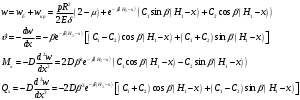 Сферическая оболочка 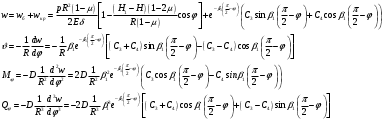 Здесь следует отметить, что угол поворота нормали в безмоментной сферической оболочке определяется по формуле 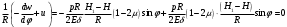 и равен нулю. Из четырёх условий стыка двух оболочек 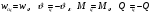 получим значения 4-х констант интегрирования при получим значения 4-х констант интегрирования при 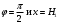 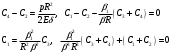 Исходные данные: 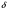 =2,5мм, толщина оболочки, R=0,5м, Н=1,5м, H1=2,0м, p =3атм избыточное давление (наддув), =2,5мм, толщина оболочки, R=0,5м, Н=1,5м, H1=2,0м, p =3атм избыточное давление (наддув), 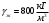 удельный вес жидкости. удельный вес жидкости.Материал оболочки – дюралевый сплав, Е=72 Гпа Посчитаем некоторые параметры, опираясь на исходные данные. 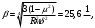 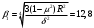 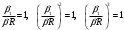 , , 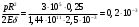 В результате решения системы алгебраических уравнений по определению констант С1 – С4 получим 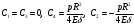 Окончательное решение для цилиндрической оболочки 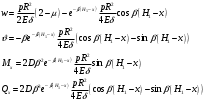 и для сферической оболочки 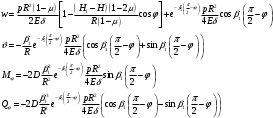  Э «w»   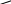  Э «u» 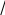    0              |
