Сопромат. Задача Для балки (рис. 5) построить эпюры внутренних усилий Q
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
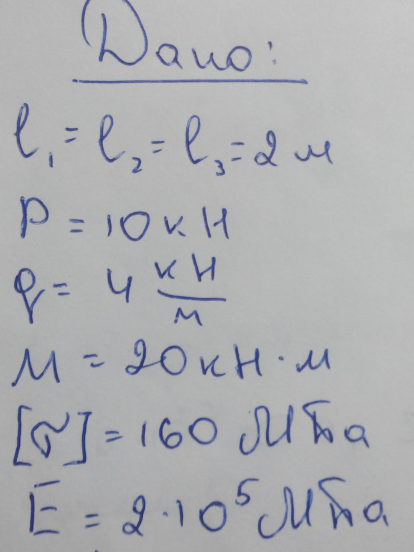 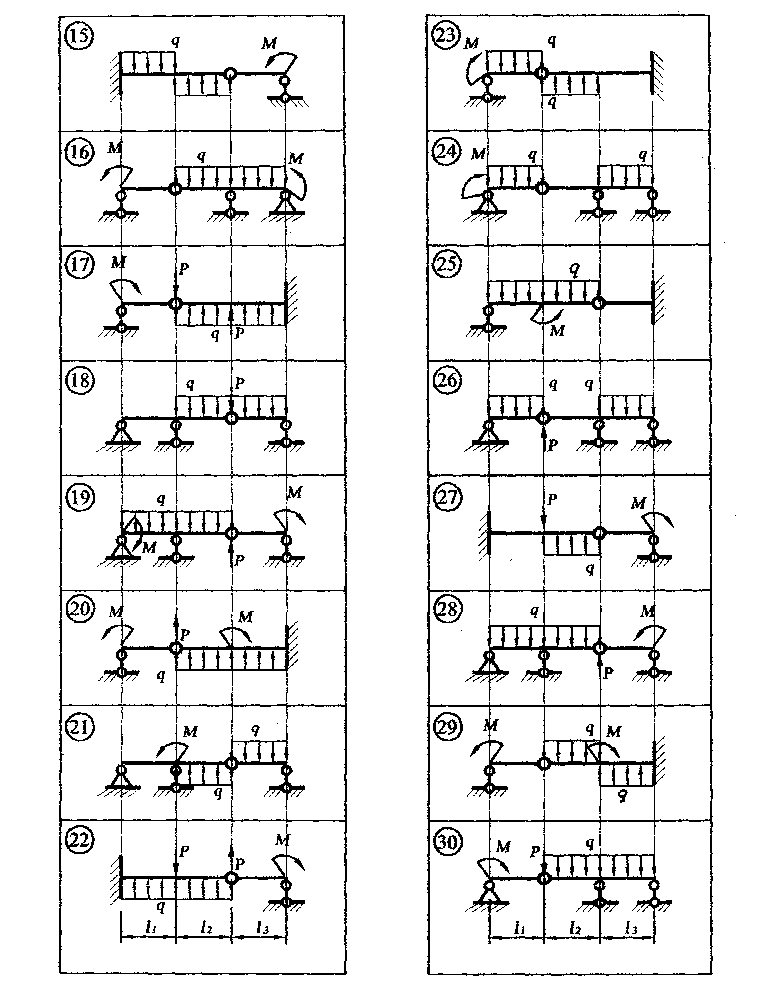 Задача 1.5. Для балки (рис. 5) построить эпюры внутренних усилий Qy и Mx, используя метод сечений, и проверить правильность их построения с помощью правил Журавского. Из условия прочности по нормальным напряжениям подобрать поперечные сечения двух видов: 1— прямоугольное с отношением сторон h/b= ; 2 — двутавровое. 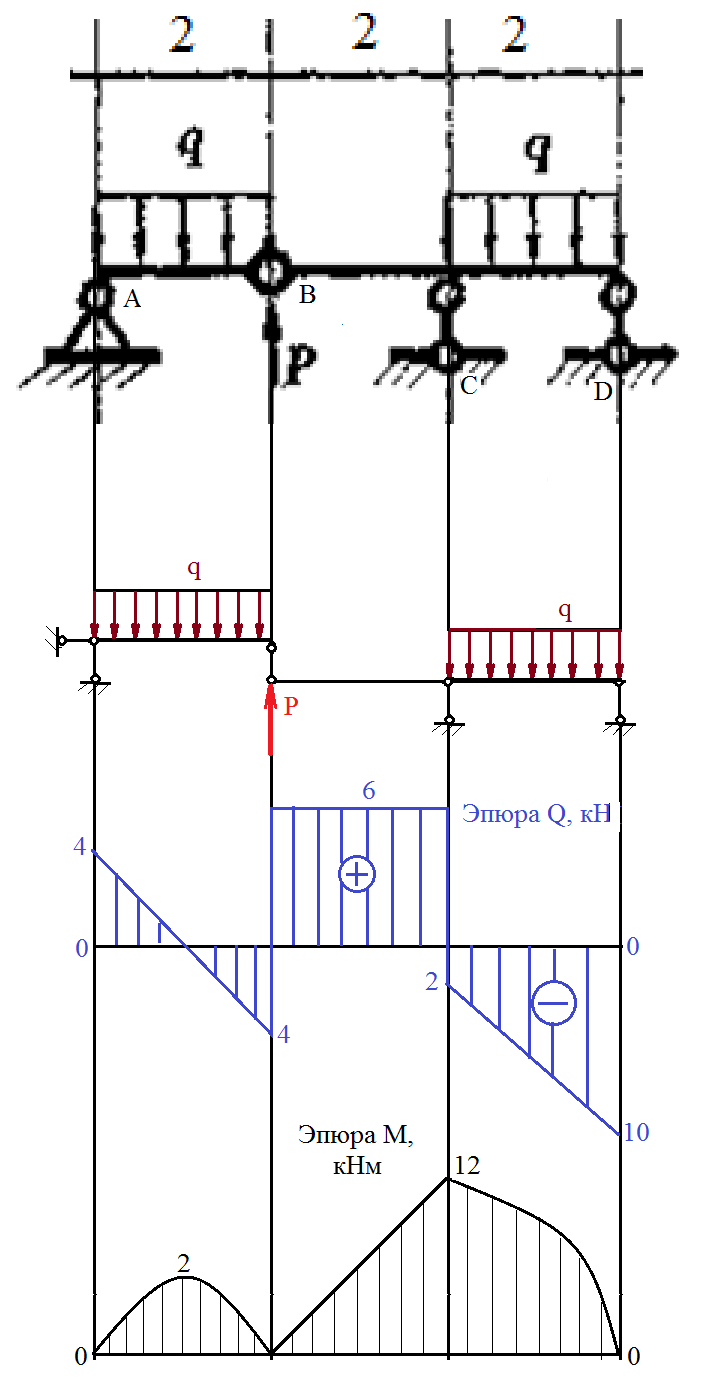 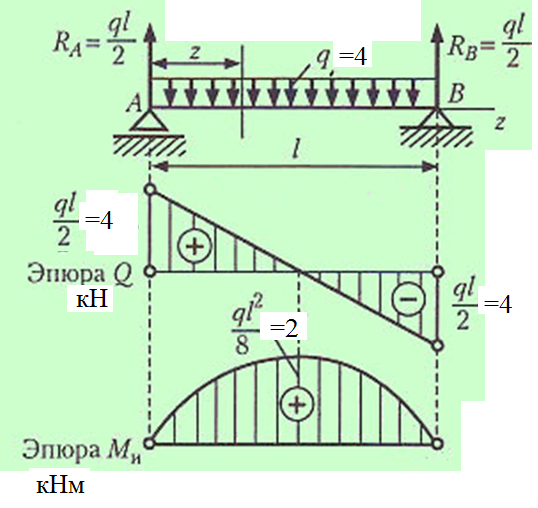 Правильность построения эпюр проверим с помощью теоремы Журавского. Как известно из математики, если Ми =ƒ(z), то dMи /dz = tg α, где α – угол, который составляет касательная к эпюре моментов с положительным направлением оси z. Согласно теореме Журавского, Q = dMи / dz = tg α На левой части балки угол α острый, Q > 0 и изгибающий момент на этом участке возрастает, на правой части балки угол α тупой, Q < 0 и изгибающий момент на участке убывает; В середине балки α = 0 на всем участке, то Ми = Mmax, Q = 0. На рассматриваемом участке балки действует равномерно распределенная нагрузка, поэтому эпюра моментов представляет собой параболу, а эпюра поперечных сил – наклонную прямую. Построим эпюры на правой части балки. Изобразим расчетную схему и определим реакции опор из условия статического равновесия балки: 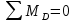 ; ; 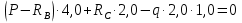 ; ; 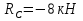 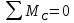 ; ;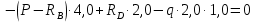 ; ; 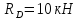 Проверка 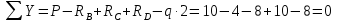 Для построения эпюр поперечных сил и изгибающих моментов воспользуемся методом сечений. Рассмотрим 2 сечения и запишем для каждого из них условия статического равновесия 1-1 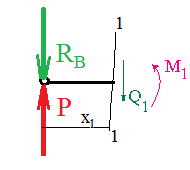 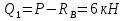 ; ; 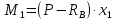 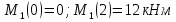 2-2 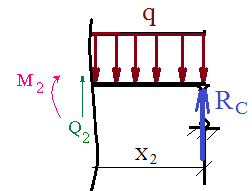 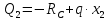 ; ; 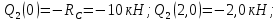 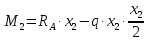 ; ;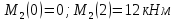  На левой части балки угол α острый, Q > 0 и изгибающий момент на этом участке возрастает, на правой части балки угол α тупой, Q < 0 и изгибающий момент на участке убывает. На левой части балки нет распределенной нагрузки, эпюра моментов представляет собой наклонную прямую, а эпюра поперечных сил – прямую, параллельную оси балки. На правой части балки действует равномерно распределенная нагрузка, поэтому эпюра моментов представляет собой параболу, а эпюра поперечных сил – наклонную прямую. Из условия прочности по нормальным напряжениям определим номер двутавра. Величина максимальных изгибающих напряжений равна 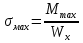 Условие прочности 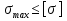 , откуда , откуда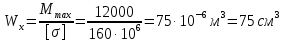 По таблице сортамента выбираем стандартный двутавр №14, для него 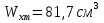 |
