Теоретические основы электротехники. ТОЭ. Задача Для электрической схемы по заданным в таблице 2 параметрам и напряжению источника определить токи во всех ветвях цепи, напряжения на отдельных участках U
 Скачать 271 Kb. Скачать 271 Kb.
|
|
Задача 2. Для электрической схемы по заданным в таблице 2 параметрам и напряжению источника определить токи во всех ветвях цепи, напряжения на отдельных участках U1-2, U2-3 и коэффициент мощности цепи cosφ. Записать аналитические выражения для мгновенных значений тока i1 и напряжения на входе схемы u. Проверить правильность расчета при помощи баланса мощностей. Построить векторную диаграмму токов и напряжений. 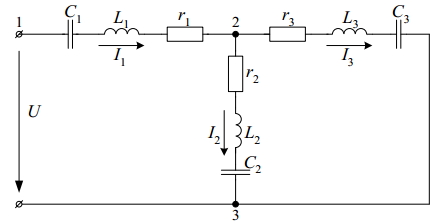  Изобразить электрическую схему для своего варианта задачи. 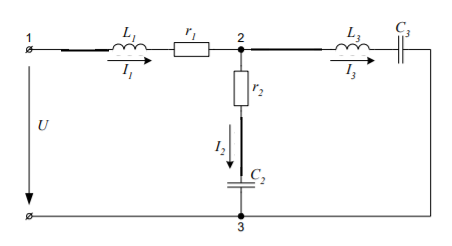 Найдем элементы реактивного сопротивления  Ом. Ом.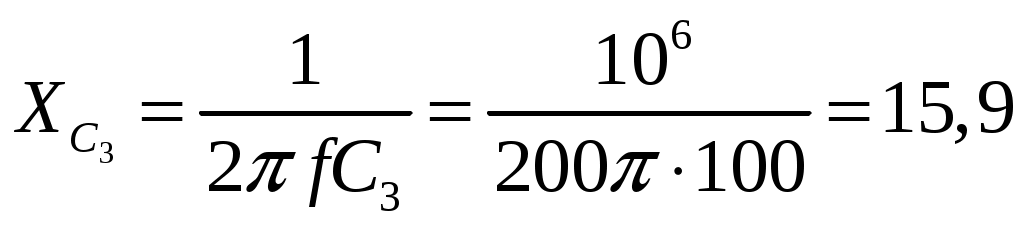 Ом. Ом.Тогда импеданс цепи есть  Ом ОмТок в цепи есть 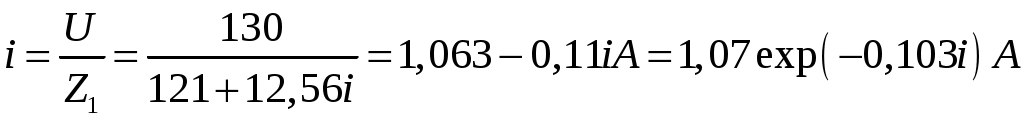 Следовательно, мгновенные значения тока и напряжения ― это Коэффициент мощности Токи в ветвях найдем, составив уравнения по первому и второму законам Кирхгофа  или или 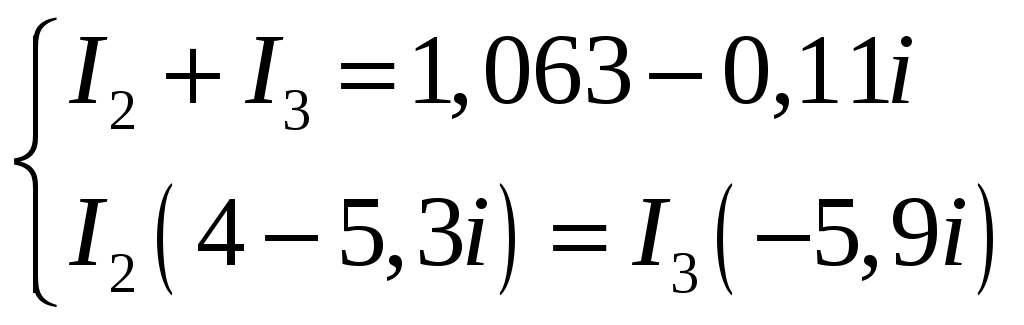 , откуда , откуда I2=0,478-0,229iA, I3=0,585+0,119i A Напряжения в цепи U12=I1Z1=(1,063-0,11i)(120+15,7i)=129,3+3,5iB U23=I2Z2=I3Z3=(0,585+0,119i)(-5,9i)=0,7-3,5iB Тогда векторная диаграмма напряжений  Видно, что в сумме векторы U12 и U23 дают вектор U=130B, т.е., задача решена верно. Векторная диаграмма токов  Мощность в цепи Видно, что P=Re(S)=138,19 Вт, Q=Im(S)=14,3 вар. Рассчитаем по отдельности активную и реактивную мощность на элементах цепи  Таким образом, баланс сошелся. Задача 3. Для электрической цепи, изображенной на рис. 21, 22, по заданным в таблице 3 параметрам и линейному напряжению определить фазные и линейные токи, ток в нейтральном проводе (для четырехпроводной схемы рис. 21), активную мощность всей цепи и каждой фазы отдельно. Построить векторную диаграмму токов и напряжений.  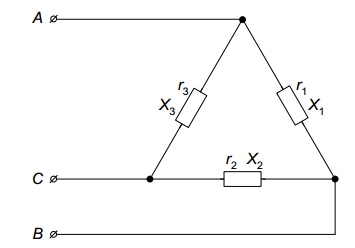 При соединении треугольником фазные напряжения равны линейным Фазные токи Активная мощность этой фазы есть 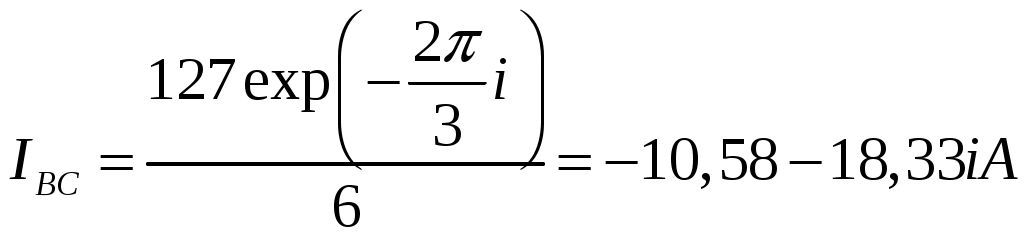 Активная мощность этой фазы есть 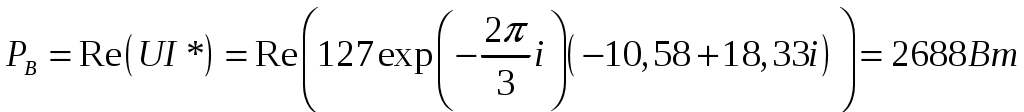 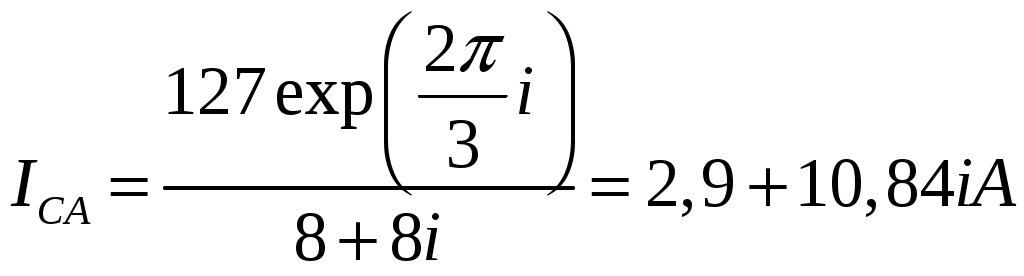 Активная мощность этой фазы есть  Чертим векторную диаграмму токов  Линейные токи строятся по фазным на основании уравнений, составленных по первому закону Кирхгофа: ÍA = Íab - Íca; = 9,43+5,6i-(2,9+10,84i)=6,53-5,24iA ÍB = Íbc - Íab; = -10,58-18,33i – (9,43+5,6i)=-20,01-23,93i A ÍC = Íca - Íbc. = 2,9+10,84i – (-10,58-18,33i) = -21,1+20i A Мощности в фазах. 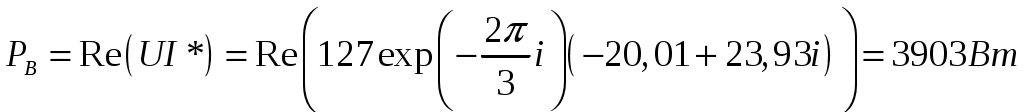 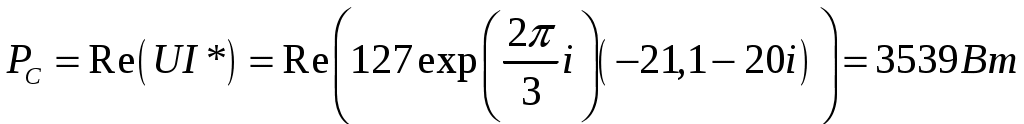 В сумме это составляет 8271 Вт. Задача 3. Для электрической цепи, изображенной на рис. 21, 22, по заданным в таблице 3 параметрам и линейному напряжению определить фазные и линейные токи, ток в нейтральном проводе (для четырехпроводной схемы рис. 21), активную мощность всей цепи и каждой фазы отдельно. Построить векторную диаграмму токов и напряжений.   При соединении звездой напряжение между линейным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя линейными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями: Фазное напряжение есть UФ= 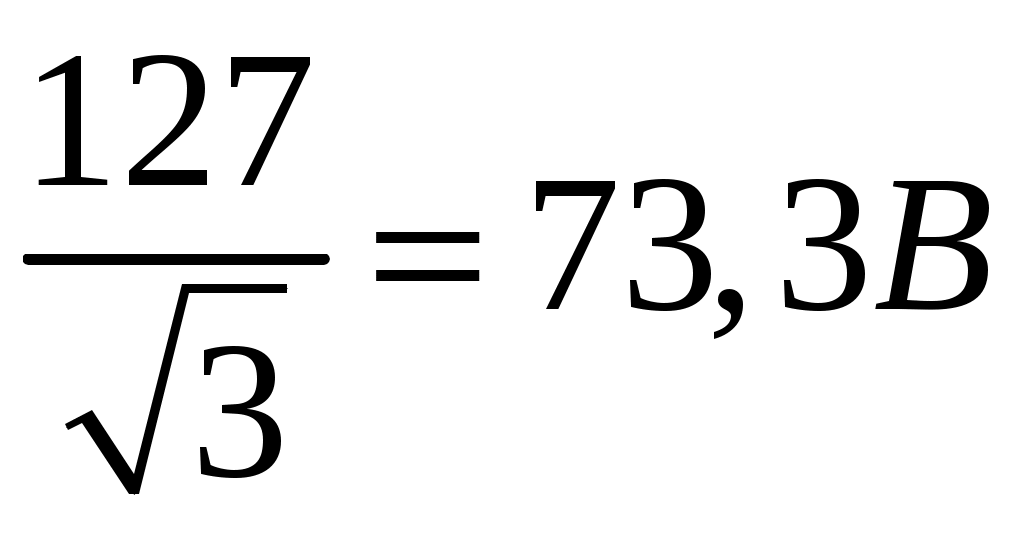 Фазные токи (они же линейные) Активная мощность этой фазы есть  Активная мощность этой фазы есть 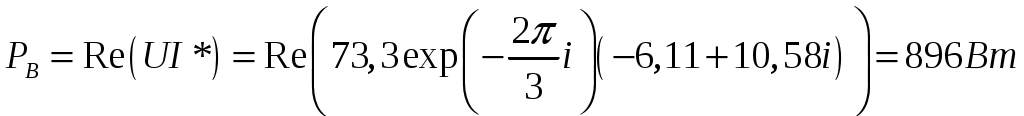 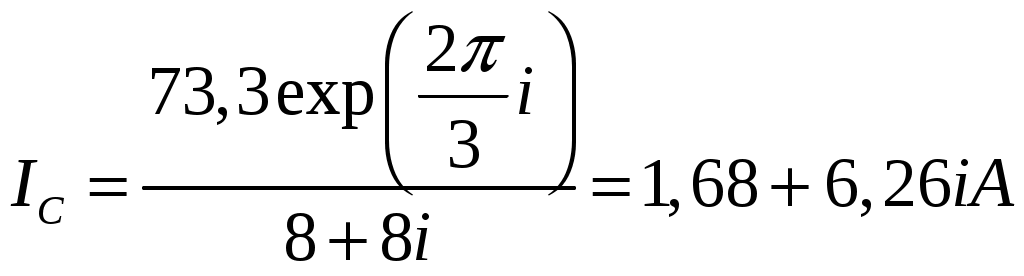 Активная мощность этой фазы есть  В сумме это составляет 1627 Вт. Чертим векторную диаграмму токов 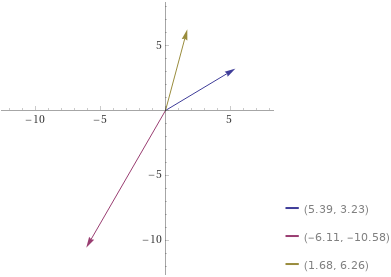 По ней выходит, что ток нейтрали есть IN=0,96-1,09i A |
