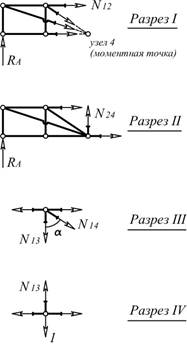
практические вар 12. Задача Для рамы, изображенной на рис. 39, назначить основные конструктивные размеры и определить расчетные максимальные усилия М, q и n при действии на нее равномерно распределенной нагрузки q по всему пролету (или на половине пролета слева).
 Скачать 241.46 Kb. Скачать 241.46 Kb.
|
|
Задача 9.1. Для рамы, изображенной на рис.39, назначить основные конструктивные размеры и определить расчетные максимальные усилия М, Q и N при действии на нее равномерно распределенной нагрузки q по всему пролету (или на половине пролета слева). Исходные данные взять из табл.40. 1.1. Определение опорных реакций Для определения опорной реакции А воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки В): ΣМВ = Al - ql2/2 = 0 (1) тогда Аl = ql2/2; ( A = ql2/2l = 12,4·1,6/2 = 9,82 кН (1) Для определения опорной реакции В также воспользуемся третьим уравнением статического равновесия системы (уравнением моментов относительно точки А): ΣМА = Вl - ql2/2 = 0 (2) тогда Вl = ql2/2; В = ql2/2= 12,4·1,6/2 = 9,92 кН Для проверки воспользуемся вторым уравнением статического равновесия системы: ∑у = ql - А - В = 0 12,4·1,6 – 12,4 – 12,4 = 0 Условие выполняется. В точке А поперечные силы условно равны нулю. Уравнение поперечных сил будет иметь следующий вид: "Q" = А - qx где х - расстояние от начала координат (точки А) до рассматриваемого сечения балки. Соответственно на расстоянии 0 м от точки А поперечные силы будут равны: "Q"А = 12,4 - 2·0 = 12,4 кН в точке В: "Q" = А - ql + В = 12,4 - 2·12,4 + 12,4 = 0 Этих данных достаточно для построения эпюр поперечных сил. 2.1. Определение изгибающих моментов Для определения изгибающих моментов, действующих в поперечных сечениях балки, используется метод сечений, согласно которому уравнение моментов будет иметь следующий вид: М = Ах - qx2/2 тогда МА = А·0 - q02/2 = 0 в середине пролета: М = Аl/2 -q(l/2)2/2 = 9,52 кНм в точке В (в конце балки): М = Al - ql2/2 = ql·l/2 - ql2/2 = 0 2.2 Определение углов поворота и прогибов поперечного сечения. Уравнение углов поворота - результат интегрирования уравнения моментов. А как известно, при интегрировании появляется постоянная интегрирования, в данном случае начальный угол поворота ΘА, который в данном случае не равен нулю. Кроме того на значение углов поворота и прогибов влияет жесткость рассматриваемой балки, выражаемая через ЕI, т.е. чем больше жесткость балки (модуль упругости и момент инерции) тем меньше в итоге углы поворота и прогибы. Уравнение углов поворота для нашей балки будет выглядеть так: θx = ∫Mdx/EI = - ΘА + Ax2/2EI - qx3/6EI Уравнение прогибов - это в свою очередь результат интегрирования уравнения углов поворота на рассматриваемом участке: fх = ∫ΘАdx = - θAx + Ax3/6EI- qx4/24EI В данном случае постоянная интегрирования - начальный прогиб - равна нулю и это логично - на опорах прогиба быть не может (во всяком случае в теории). Это позволяет составить дополнительное уравнение прогиба для одной из опор, например для точки В уравнение прогиба будет иметь вид: fВ = - θAl + Al3/6EI - ql4/24EI = 0 тогда θAl = Al3/6EI - ql4/24EI θA = ql3/(2·6EI) - ql4/(l·24EI) θA = ql3/24EI = 36,6/EI Так как у нас симметричны и балка и нагрузка, что мы уже заметили раньше, то конечный угол поворота поперечного сечения (на опоре В) будет равен начальному углу поворота. Проверяем правильность вычислений: θB = - ΘА + Al2/2EI - ql3/6EI = (-14.971 + 87.8238 - 51.9125)/EI = 18.932/EI Так как у нас симметричные и балка и нагрузка, то нет необходимости определять точку, где прогиб максимальный. Это сечение будет посредине балки. fmax = - θВ2.3 + В·2.33/6EI - q2.34/24EI = - 18.932/ЕI fmax = - θА2.3 + А·2.33/6EI - q2.34/24EI = - 18.932/ЕI Чтобы эпюры углов поворота и прогибов были универсальными и подходили и для деревянных и для стальных и для железобетонных и для каких угодно других балок, на эпюрах показываются не абсолютные значения, а относительные. Т.е. обе части уравнения умножаются на ЕI. 2.3. Построение эпюр поперечных сил и изгибающих моментов: На основании полученных ранее данных строим эпюры: 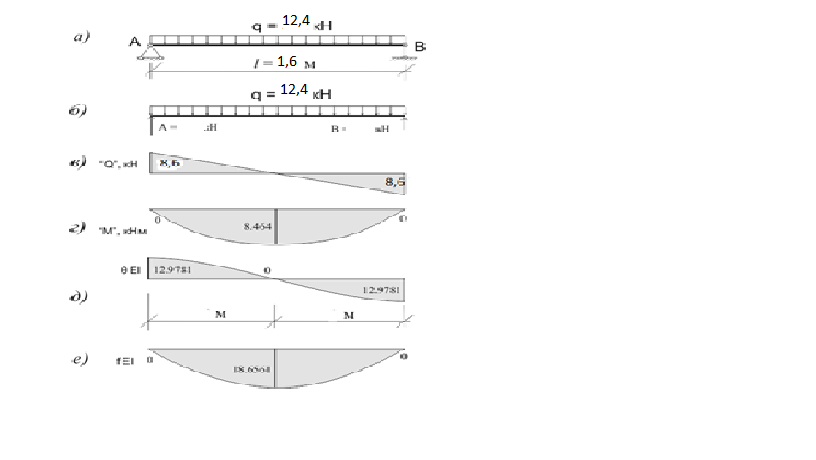 Рисунок 1. Расчетная схема (а), замена опор на реактивные силы (б), эпюра поперечных сил (в), эпюра изгибающих моментов (г), эпюра углов поворота (д), эпюра прогибов (е). На эпюре поперечных сил в начале координат (в точке А) откладываем вверх значение опорной реакции А, согласно направлению действия реактивной силы (опорной реакции. В точке В откладываем значение опорной реакции вниз. Соединяем полученные точки прямой. "Q"х→l = Аl - ql = - 12,4 кН (671.9) А в точке В, где приложена реактивная сила (опорная реакция В) на эпюре происходит скачок (как впрочем и в точке А) т.е. формально мы все-таки откладываем опорную реакцию вверх и таким образом все, как положено. Так как у нас балка на шарнирных опорах, на которую действует только равномерно распределенная нагрузка, то значения моментов на опорах равны нулю, что мы и определили ранее. На эпюре моментов посредине пролета (на расстоянии 2.3 м от начала координат) откладываем вниз значение максимального момента. Соединяем эти точки кривой линией, как показано на рисунке. В общем-то как уже говорилось, эта кривая линия - квадратичная парабола и формально для ее построения можно определить сколь угодно много значений моментов для различных сечений. Задача 10.1. Определить усилие в элементах ферм, изображенных на рис.42, при загружении их нагрузкой, показанной на рис.43. Исходные данные взять из табл.46.
б) Линии влияния усилий для отмеченных на схеме стержней 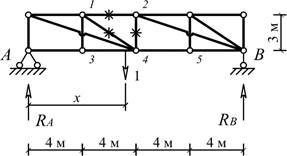 Рис. 3
 Рис. 4 в) Определение усилий в отмеченных стержнях по формуле влияния от сил F=3 кН. N12=3∙(-2/3)+3∙(-4/3)+3∙(-2/3)=-8 кН, N24=3∙(1/4)+3∙(1/2)+3∙(-1/4)=1,5 кН, N13=3∙1=3 кН, N14=3∙(-5/3)=-5 кН. 11.1 Подобрать рациональное пространственное покрытие для здания, не имеющего внутренних опор (опоры есть только по контуру здания). Дать общий вид этой конструкции (план, разрезы), указать, из каких элементов она состоит и как увязываются эти элементы в общем пространственном покрытии. 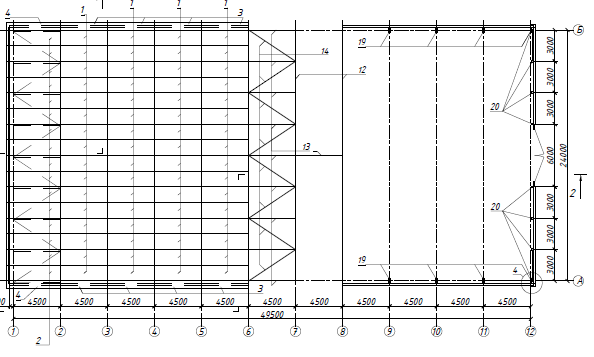 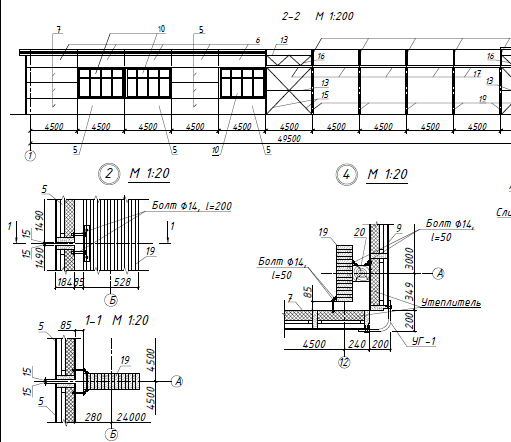 12.1 Нижний, растянутый пояс срермы получил дефект, потерял несущую способность и требует усиления. Усиление выполнено с помощью стального хомута (рис.45). Подобрать диаметр хомута и количество нагелей для крепления накладок при условии полного восстановления несущей способности пояса. Исходные данные взять из табл.51. Решение Nx = φxRcA, Nv = φyRcA. Необходимые величины для их подсчета: = bh = 17,5*15 = 262,5 см2; Несущая способность колонны N = 0,617*13*262,5*103 = 2105 кН: При изменении условий эксплуатации с группы А1 на группу В2 необходимо расчетное сопротивление умножить на коэффициент m в= 0,85. Тогда несущая способность колонны будет равна: N = φxmвRcA = 0,617*0,85*13*262,5*103 = 1800 кН. Колонну нужно усилить на дополнительную нагрузку N = 2105-1800 = 305 кН, причем это сделать нужно в двух плоскостях, так как Nx = Ny. Усиливаем колонну путем прикрепления к ней дополнительного элемента сечением 75x262,5 мм. Крепление осуществляем болтами диаметром 16 мм с шагом расстановки по длине колонны, равным 500 мм (рис.). 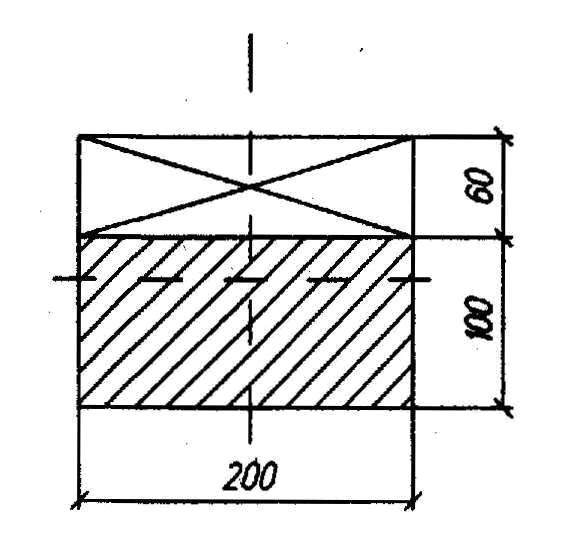 Рис.. Поперечное сечение усиленной колонны Для него имеем: 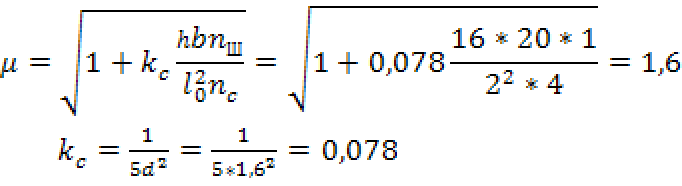 Где (см.табл. 22П приложения); nс — 4 -количество срезов нагеля на 1 пог. м. Приведенная гибкость стержня (при l1 = 500 мм > 7δ = 7*60 = 420) 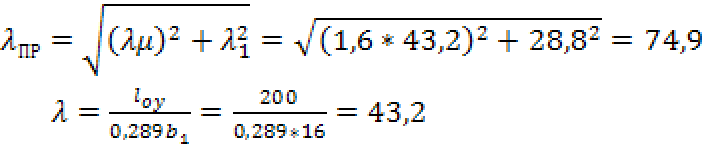 где Коэффициент φ при lпр > 70 Проверка несущей способности: Устойчивость в плоскости оси у обеспечена. Проверка устойчивости усиленной колонны в плоскости оси х: где φx = 1 - 0,8(69,2/100)2 = 0,617, определен по гибкости Устойчивость колонны обеспечена. |