Контрольная по электротехнике 12.1, 12.2,12.3, 12.4 В35 2 Марат. Задача. Для заданной электрической схемы и значений параметров ее элементов (табл. 12. 1) выполнить следующее
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
12.4 Переходные процессы в линейных электрических цепях Задача. Дана электрическая цепь, в которой происходит коммутация. Требуется определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжение на каком-либо элементе или между заданными точками схемы. Задачу решается классическим методам. Таблица 12.4 Параметры элементов электрической цепи
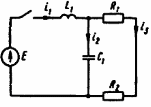 Рис. 12.72 Классический метод. Расчет цепи до коммутации и определение начальных условий: токов в индуктивностях и напряжений на емкостях. До коммутации ток в цепи постоянный, поэтому емкость заменяем разрывом цепи, а индуктивность – перемычкой. Решение задачи получается в виде суммы принужденного и свободного параметра: i(t) = iпр(t) + iсв(t); u(t) = uпр(t)+ uсв(t), (1) где 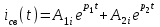 , а , а 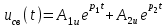 . .Находим токи и напряжения докоммутационного режима для момента времени t = (0–). Так как сопротивление индуктивности постоянному току равно нулю, а емкости – бесконечности, то расчетная схема будет выглядеть так, как это изображено на рис. 2.     Расчет цепи, сложившейся после коммутации и определение принужденной составляющей решения. После коммутации ток также постоянен, поэтому можем также заменить емкость разрывом цепи, а индуктивность – перемычкой.    Индуктивность закорочена, ветвь с емкостью исключена. Так как в схеме все ветви разорваны, то ток i1(0–) =0, ток i2(0–)=0, ток i3(0–)=0. В схеме при t(0–) контура нет. UC1(0–) = 0 В       Индуктивность закорочена, ветвь с емкостью исключена. В схеме после коммутации образовался контур. 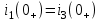 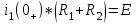 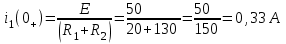 UC1(0+) = Е=50 В Составление системы дифференциальных уравнений    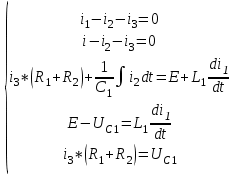 Решение системы дифференциальных уравнений. 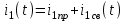 Значение принужденной составляющей тока 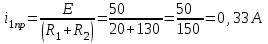 Определение свободной составляющей тока при помощи входного сопротивления цепи  L1(р)       1/C1(р) Zвх(р)  Составление характеристического уравнения цепи, отыскание его корней. Из цепи, сложившейся после коммутации, исключаем источник энергии, заменяя его перемычкой. Производим разрыв цепи в любой, произвольно выбранной, точке. Заменяем элементы цепи их комлексными сопротивлениями, произведение jω заменяем на p. Определяем входное сопротивление полученной цепи относительно точек разрыва. Приравниваем найденное сопротивление нулю и определяем p – корни характеристического уравнения. Нахождение постоянных интегрирования на основе законов коммутации. Определение других токов или напряжений в цепи. 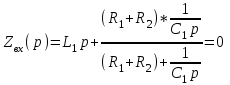 откуда получаем характеристическое уравнение 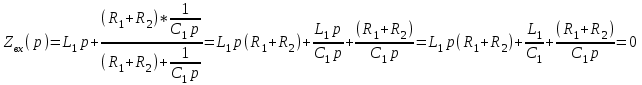 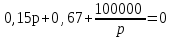 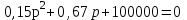 Для решения квадратного уравнения можно использовать формулы:  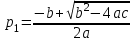 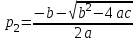 Корни характеристического уравнения 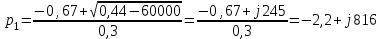 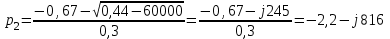 δ=2,2 с-1; ω0=816 с-1 φ=89,850 Характер переходного процесса при комплексно-сопряженных корнях определяется выражением: Находим установившиеся значения требуемых величин. Рисуем эквивалентную схему по прошествии большого количества времени. Ключ сработал, все переходные процессы завершены. На постоянном токе индуктивность эквивалентна закоротке, ёмкость разрыву:   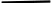    Установившееся значение искомого тока: ic уст=0 А Анализ докоммутационного состояния для нахождения сохраняющихся величин: напряжения на ёмкости и тока через индуктивность. На постоянном токе индуктивность эквивалентна закоротке, ёмкость разрыву.  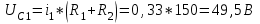 Анализ начальных условий нулевого порядка. Рассматривается момент времени сразу после коммутации. По законам коммутации можно записать: 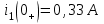 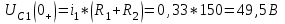 Тогда: 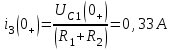 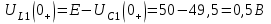 Анализ начальных условий первого порядка (производных от начальных величин). Рассматривается момент времени сразу после коммутации. Т.к. ЭДС постоянна, а эквивалентная схема рисуется для производных величин, то источник будет отсутствовать. 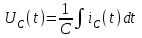 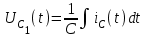 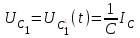 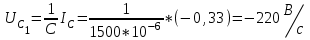 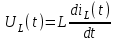 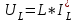 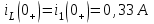 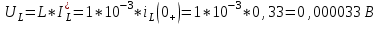 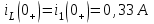 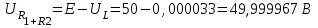 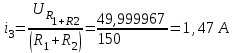 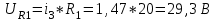 | ||||||||||||||||||

 ,мГн
,мГн