Контрольная по электротехнике 12.1, 12.2,12.3, 12.4 В35 2 Марат. Задача. Для заданной электрической схемы и значений параметров ее элементов (табл. 12. 1) выполнить следующее
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
2. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКАКонтрольное задание Задача. Для электрической схемы, изображенной на рис.2.1, выполнить следующее: 1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух формах: а) дифференциальной; б) символической. 2. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей. 3. По результатам, полученным в п. 2, определить показания ваттметра двумя способами: а) с помощью выражения для комплексов тока и напряжения на ваттметре; б) по формуле UIcos. С помощью векторной диаграммы тока и напряжения, на которые реагирует ваттметр, пояснить определение угла = u - i. 4. Построить топографическую диаграмму, совмещенную с векторной диаграммой токов. При этом потенциал точки a, указанной на схеме, принять равным нулю. 5. Построить круговую диаграмму для тока в одном из сопротивлений цепи при изменении модуля этого сопротивления в пределах от нуля до бесконечности. Сопротивление, подлежащее изменению, отмечено в таблице звездочкой (*). На схеме следует его перечеркнуть стрелкой. 6. Пользуясь круговой диаграммой, построить график изменения тока в изменяющемся сопротивлении в зависимости от модуля этого сопротивления. 7. Используя данные расчетов, полученных в п.2 или 5, записать выражения для мгновенного значения заданного тока или напряжения. Построить график зависимости указанной величины от t. 8. Полагая, что между любыми двумя индуктивными катушками, расположенными в различных ветвях схемы заданной схемы, имеется магнитная связь при коэффициенте взаимной индукции, равном M, составить в общем виде систему уравнений по законам Кирхгофа для расчета токов во всех ветвях схемы, записав ее в двух формах: а) дифференциальной; б) символической. Указания: 1. Ориентируясь на ранее принятые направления токов в ветвях, одноименные зажимы индуктивных катушек выбрать по своему усмотрению так, чтобы было их встречное включение, и обозначить на схеме эти зажимы звездочками (точками). 2. В случае отсутствия в заданной схеме второй индуктивности вторую катушку ввести дополнительно в одну из ветвей, не содержащих L. 12.2. Электрические цепи синусоидального токаТаблица 12.2 Варианты задания
В табл. 12.2 приведены амплитудные значения и начальные фазы в градусах источников ЭДС Emiи φi. Мгновенное значение ЭДС ei = Emi sin(ω t+ φi).       I3 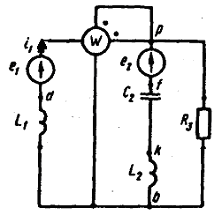 Рис. 12.23 1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух формах: а) дифференциальной; б) символической. Данная схема имеет два узла (m=2) и три обобщенных ветвей (n=3). Число независимых контуров, равное числу ветвей связи, с=n-m+1=2. Составим систему уравнений для узлов a,d: 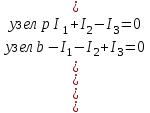
Система уравнений в дифференциальной форме: 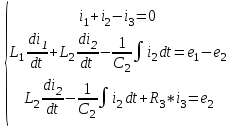 Система уравнений в символической форме: 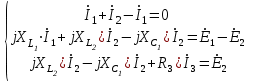 2. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей. 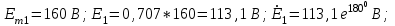 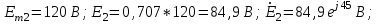 Для расчёта токов в ветвях воспользуемся методом междуузлового напряжения. 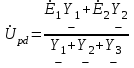 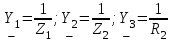 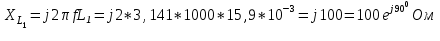 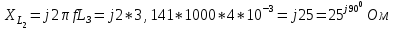 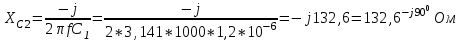 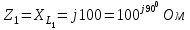 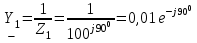 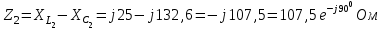 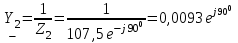 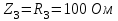 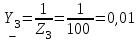 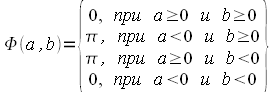 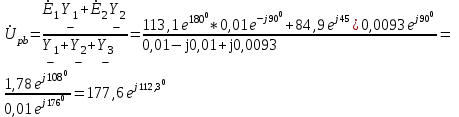 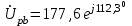 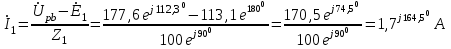 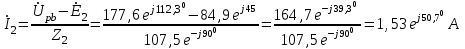 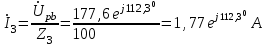 Проверка 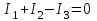 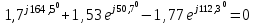 Условие выполнено. 3. По результатам, полученным в п. 2, определить показания ваттметра двумя способами: а) с помощью выражения для комплексов тока и напряжения на ваттметре; б) по формуле UIcos. С помощью векторной диаграммы тока и напряжения, на которые реагирует ваттметр, пояснить определение угла = u - i. 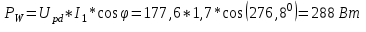     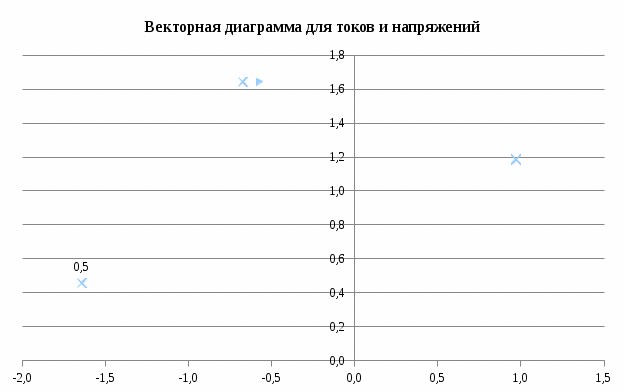 12.3 Трехфазные цепи Задача.Для электрической цепи, схема которой изображена на рис. 12.41–12.57, по заданным в табл. 12.3 параметрам и линейному напряжению, определить фазные и линейные токи, ток в нейтральном проводе (для четырехпроводной схемы), активную мощность всей цепи и каждой фазы отдельно. Построить векторную диаграмму токов и напряжений на комплексной плоскости. Таблица 12.3 Варианты задания
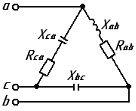 Рис. 12.56 Многофазная цепь является не симметричной, так как комплексные сопротивления соответствующих фаз не одинаковы. Полное сопротивление участка ab: 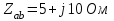 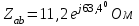 Полное сопротивление участка bc: 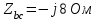 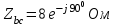 Полное сопротивление участка cа: 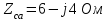 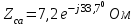 Известны сопротивления треугольника Zcb, Zbc, Zab, то для сопротивления эквивалентной звезды получаем: 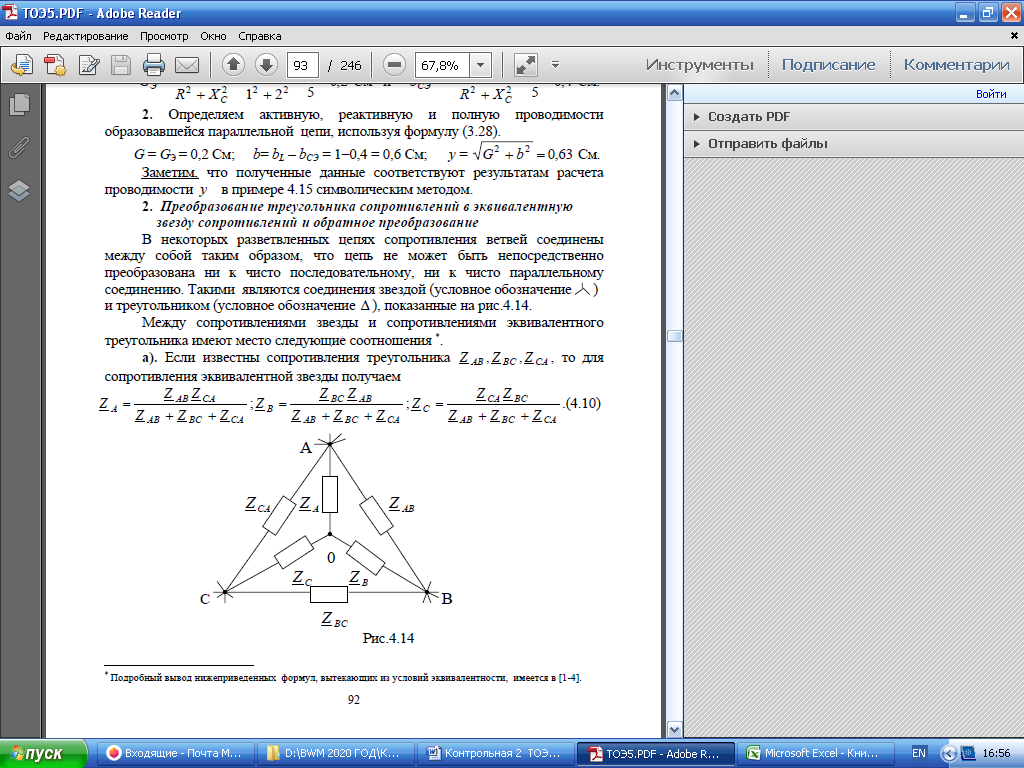  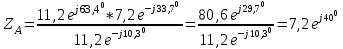 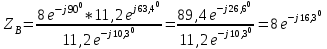 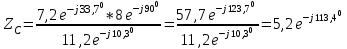 Фазные напряжения: 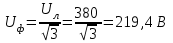 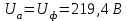 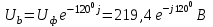 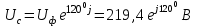 Тогда линейные токи 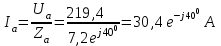 в алгебраической форме 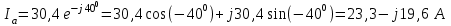 Угол сдвига фаз 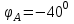 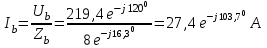 в алгебраической форме 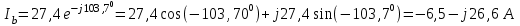 Угол сдвига фаз 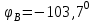 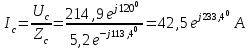 в алгебраической форме 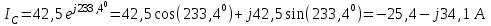 Угол сдвига фаз 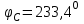 ток в нейтральном проводе определяется как геометрическая сумма линейных токов 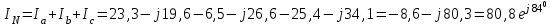 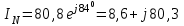 Углы сдвига фаз между векторами тока и напряжения 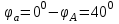 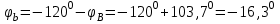 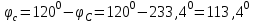 Определим суммарную активную реактивную и полную мощности Активные мощности для каждой ветки 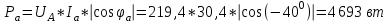 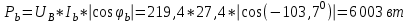 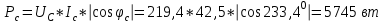 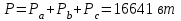 Реактивные мощности 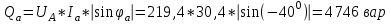 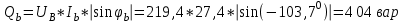 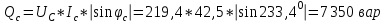 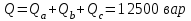 Полная мощность 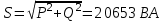 Построим векторную диаграмму для токов и напряжений 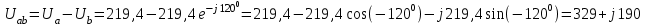 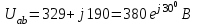 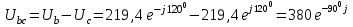 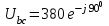 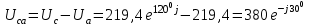 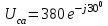 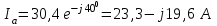 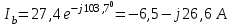 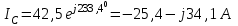 Масштаб токов 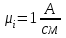 Масштаб напряжений: 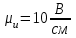       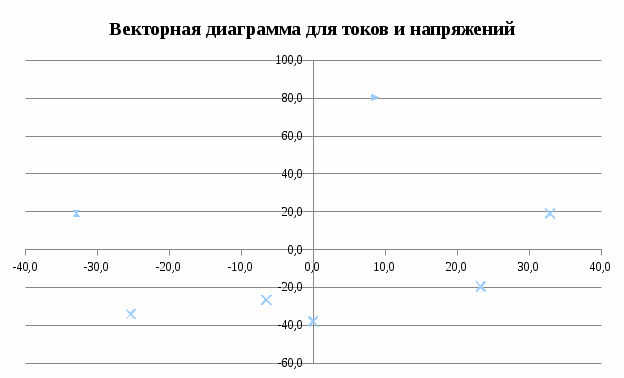 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
