математика. Задача это сформулированный словами вопрос, ответ на который требует выполнения арифметических действий
 Скачать 97.6 Kb.
|
|
1. Структура текстовой задачи Задача – это сформулированный словами вопрос, ответ на который требует выполнения арифметических действий. Текстовая задача представляет собой описание какого-либо явления (ситуации, процесса). С этой точки зрения текстовая задача есть словесная модель явления (ситуации, процесса). И, как во всякой модели, в текстовой задаче описывается не все явление в целом, а лишь некоторые его стороны, главным образом, его количественные характеристики. Рассмотрим, например, такую задачу: «Автомобиль выехал из пункта А со скоростью 60 км/ч. Через 2 ч вслед за ним выехал второй автомобиль со скоростью 90 км/ч. На каком расстоянии от А второй автомобиль догонит первый?» В задаче описывается движение двух автомобилей. Как известно, любое движение характеризуется тремя величинами: пройденным расстоянием, скоростью и временем движения. В данной задаче известны скорости первого и второго автомобилей (60 км/ч и 90 км/ч), известно, что они прошли одно и то же расстояние от пункта А до места встречи, количественную характеристику которого и надо найти. Кроме того, известно, что первый автомобиль был в пути на 2 ч больше, чем второй. Обобщая, можно сказать, что текстовая задача есть описание на естественном языке некоторого явления (ситуации, процесса) с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения. Чтобы выяснить, как построена текстовая задача рассмотрим следующий пример из начального курса математики: «Свитер, шапку и шарф связали из 1 кг 200 г шерсти. На шарф потребовалась на 100 г шерсти больше, чем на шапку, и на 400 г меньше, чем на свитер. Сколько шерсти израсходовали на каждую вещь?» В задаче речь идет о свитере, шапке и шарфе. Это объекты задачи. Относительно этих объектов имеются определенные утверждения и требования. Утверждения: 1. Свитер, шапка и шарф связаны из 1200 г шерсти. 2. На шарф израсходовали на 100 г больше, чем на шапку. 3. На шарф израсходовали на 400 г меньше, чем на свитер. Требования: 1. Сколько шерсти израсходовали на свитер? 2. Сколько шерсти израсходовали на шапку? 3. Сколько шерсти израсходовали на шарф? Утверждения задачи называют условиями (или условием, как в начальной школе). В задаче обычно не одно условие, а несколько элементарных условий. Они представляют собой количественные или качественные характеристики объектов задачи и отношений между ними. Требований в задаче может быть несколько. Они могут быть сформулированы как в вопросительной, так и утвердительной форме. Условия и требования взаимосвязаны. Систему взаимосвязанных условий и требований называют высказывательной моделью задачи. Таким образом, чтобы понять, какова структура задачи, надо выявить ее условия и требования, отбросив все лишнее, второстепенное, не влияющее на ее структуру. Иными словами, надо построить высказывательную модель задачи. Чтобы получить эту модель, надо текст задачи развернуть (сделать это можно письменно или устно), так как текст задачи, как правило, дается в сокращенном, свернутом виде. Для этого можно перефразировать задачу, построить ее графическую модель, ввести какие-либо обозначения и т.д. Итак, составные части задачи: условие, вопрос, решение, ответ. По отношению между условиями и требованиями различают: а) определенные задачи - в них заданных условий столько, сколько необходимо и достаточно для выполнения требований; б) недоопределенные задачи - в них условий недостаточно для получения ответа; в) переопределенные задачи - в них имеются лишние условия. В начальной школе недоопределенные задачи считают задачами с недостающими данными, а переопределенные - задачами с избыточными данными. Например, задача «Возле дома росло 5 яблонь, 2 вишни и 3 березы. Сколько фруктовых деревьев росло возле дома?» является переопределенной, так как содержит лишнее условие. Задача «Из зала вынесли сначала 12 стульев, потом еще 5. Сколько стульев осталось в зале?» является недоопределенной - в ней условий недостаточно, чтобы ответить на поставленный вопрос. Уточним теперь смысл термина «решение задачи». Так сложилось, что этим термином обозначают разные понятия: 1) решением задачи называют результат, т.е. ответ на требование задачи; 2) решением задачи называют процесс нахождения этого результата, причем этот процесс рассматривают двояко: и как метод нахождения результата (например, говорят о решении задачи арифметическим способом) и как последовательность тех действий, которые выполняет решающий, применяя тот или иной метод (т.е. в данном случае под решением задачи понимается вся деятельность человека, решающего задачу). 2. Методы и способы решения текстовых задач Основными методами решения текстовых задач являются арифметический и алгебраический. Кроме этого есть графический и практический. Решить задачу арифметическим методом - это значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу можно решить различными арифметическими способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи. Решим, например, различными арифметическими способами такую задачу: «Сшили 3 платья, расходуя на каждое по 4 м ткани. Сколько кофт можно было сшить из этой ткани, если расходовать на одну кофту 2 м?» 1 способ 1)4 ∙ 3= 12 (м) - столько было ткани; 2) 12:2 = 6 (кофт) - столько кофт можно сшить из 12 м ткани. 2 способ 1)4:2 = 2 (раза) - во столько раз больше идет ткани на платье, чем на кофту; 2) 3 ∙ 2 = 6 (кофт) - столько кофт можно сшить. Решить задачу алгебраическим методом - это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. Если для одной и той же задачи можно составить различные уравнения (системы уравнений), то это означает, что данную задачу можно решить различными алгебраическими способами. Например, задачу о массе шерсти, израсходованной на свитер, шапку и шарф (с. 115), можно решить тремя различными способами. 1 способ Обозначим через х (г) массу шерсти, израсходованной на шапку. Тогда на шарф будет израсходовано (х + 100) г, а на свитер ((х + 100) + 400) г. Так как на все три вещи израсходовано 1200 г, то можно составить уравнение х + (х + 100) + ((х + 100) + 400) = 1200. Выполнив преобразования, получим , что х = 200. Таким образом, на шапку было израсходовано 200 г, на шарф -300 г, так как 200+ 100 = 300, на свитер - 700 г, так как (200+ 100)+ 400 = 700. 2 способ. Обозначим через х (г) массу шерсти, израсходованной на шарф. Тогда на шапку будет израсходовано (х - 100) г, а на свитер - (х + 400) г. Поскольку на все три вещи израсходовано 1200 г, то можно составить уравнение: х + (х-100) + (х + 400)= 1200. Выполнив преобразования, получим, что х = 300. Таким образом, если на шарф израсходовали 300 г, то на шапку 200 г (300 - 100 = 200), а на свитер 700 г (300 + 400 = 700). 3 способ. Обозначим через х (г) массу шерсти, израсходованной на свитер. Тогда на шарф будет израсходовано (х - 400) г, а на шапку (х - 400 - 100) г. Поскольку на все три вещи израсходовано 1200 г, то можно составить уравнение: х + (х - 400) + (х - 500) = 1200. Выполнив преобразования, получим, что х = 700. Таким образом, если на свитер израсходовано 700 г, то на шарф пошло 300 г (700 - 400 = 300), а на шапку - 200 г (700 - 400 - 100 = 200). 3. Этапы решения задачи и приемы их выполнения Деятельность по решению задачи арифметическим методом включает следующие основные этапы: 1.Анализ задачи. 2.Поиск плана решения задачи. 3.Осуществление плана решения задачи. 4.Проверка решения задачи. В реальном процессе решения задачи названные этапы не имеют четких границ и не всегда выполняются одинаково полно. Все зависит от уровня знаний и умений решающего. 1). Анализ задачи Основное назначение этого этапа - понять в целом ситуацию, описанную в задаче; выделить условия и требования; назвать известные и искомые объекты, выделить все отношения (зависимости) между ними. Вопросы для анализа задачи. - О чем задача? - Что требуется найти в задаче? - Что обозначают те или иные слова в тексте задачи? - Что в задаче неизвестно? - Что является искомым? Большую помощь в осмыслении задачи оказывает прием - перефразировка текста задачи. Он заключается в замене данного в задаче описания некоторой ситуации другим, сохраняющим все отношения, связи, качественные характеристики, но более явно их выражающим. Это достигается в результате отбрасывания несущественной, излишней информации, замены описания некоторых понятий соответствующими терминами и, наоборот, замены некоторых терминов описанием содержания соответствующих понятий; преобразование текста задачи в форму, удобную для поиска плана решения. Составляется краткая запись задачи. Виды кратких записей: 1) краткая запись в виде таблицы. 2) краткая запись с помощью опорных слов 3) краткая запись с помощью чертежа Например. 1. Таблица
2. С опорными словами  Было – 18 ябл.Съели – 5 ябл. Осталось - ? ябл. 3.С помощью чертежа После построения вспомогательной модели необходимо проверить: 1) все ли объекты задачи показаны на модели; 2) все ли отношения между объектами отражены; 3) все ли числовые данные приведены; 4) есть ли вопрос (требование) и правильно ли он указывает искомое? 2). Поиск и составление плана решения задачи Назначение этого этапа: установить связь между данными и исходными объектами, наметить последовательность действий. Поиск плана решения задачи является трудным процессом, который точно не определен. Можно только указать некоторые приемы, которые позволят осуществлять этот этап. Одним из наиболее известных приемов поиска плана решения задачи арифметическим способом является разбор задачи по тексту или по ее вспомогательной модели. Разбор задачи проводится в виде цепочки рассуждений, которая может начинаться от данных задачи, так и от ее вопросов. При разборе задачи от данных к вопросу решающий выделяет в тексте задачи два данных и на основе знания связи между ними (такие знания должны быть получены при анализе задачи) определить, какое неизвестное может быть найдено по этим данным и с помощью какого арифметического действия. Затем, считая это неизвестное данным, решающий вновь выделяет два взаимосвязанных данных, определяет неизвестное, которое может быть найдено по ним и с помощью какого действия и т.д., пока не будет выяснено, какое действие приводит к получению искомого в задаче объекта. Проведем такой разбор по тексту задачи: «На поезде, который шел со скоростью 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем проехал. Каков весь путь туриста?» Рассуждения ведем от данных к вопросу: известно, что 6 ч турист проехал на поезде, который шел со скоростью 56 км/ч; по этим данным можно узнать расстояние, которое проехал турист за 6 ч, - для этого достаточно скорость умножить на время. Зная пройденную часть расстояния и то, что оставшееся расстояние в 4 раза больше, можно найти, чему оно равно. Для этого пройденное расстояние нужно умножить на 4 (увеличить в 4 раза). Зная, сколько километров турист проехал и сколько ему осталось ехать, можем найти весь путь, выполнив сложение найденных отрезков пути. Итак, первым действием будем находить расстояние, которое турист проехал на поезде; вторым действием - расстояние, которое ему осталось проехать; третьим - весь путь. При разборе задачи от вопроса к данным нужно обратить внимание на вопрос задачи и установить (на основе информации, полученной при анализе задачи), что достаточно узнать для ответа на этот вопрос. Для чего нужно обратиться к условиям и выяснить, есть ли для этого необходимые данные. Если таких данных нет или есть только одно данное, то установить, что нужно знать, чтобы найти недостающее данное (недостающие данные), и т.д. Потом составляется план решения задачи. Рассуждения при этом проводятся в обратном порядке. Проведем такой разбор той же задачи о движении туриста, строя цепочку рассуждений от вопроса к данным: «В задаче требуется узнать весь путь туриста. Мы установили, что путь состоит из двух частей. Значит, для выполнения требования задачи достаточно знать, сколько километров турист проехал и сколько километров ему осталось проехать. И то, и другое неизвестно. Чтобы найти пройденный путь, достаточно знать время и скорость, с которой ехал турист. Это в задаче известно. Умножив скорость на время, узнаем путь, который турист проехал. Оставшийся путь можно найти, увеличив пройденный путь в 4 раза (умножив на 4). Итак, вначале можно узнать пройденный путь, затем оставшийся, после чего сложением найти весь путь». Поиск плана решения задачи может проводиться по вспомогательной модели, выполненной при анализе задачи. Еще один способ разбора задачи – с помощью наводящих вопросов. Этот способ применяется при решении задач на нахождение неизвестного по двум разностям. 3). Осуществление плана решения задачи Назначение данного этапа - найти ответ на требование задачи, выполнив все действия в соответствии с планом. Для текстовых задач, решаемых арифметическим способом, используются следующие приемы: - запись по действиям (с пояснением, без пояснения, с вопросами); - запись в виде выражения. Приведем примеры различных записей плана решения задачи: «На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?» 1. Запись решения по действиям с пояснением к каждому выполненному действию. 1) 56 ∙ 6 = 336 (км) - турист проехал за 6 ч 2) 336 ∙ 4= 1344 (км) - осталось проехать туристу 3) 336 + 1344 = 1680 (км) - должен был проехать турист. Если пояснения даются в устной форме (или совсем не даются), то запись будет следующей: 1) 56 ∙ 6 = 336 (км) 2) 336 ∙ 4 = 1344 (км) 3) 336 + 1344 = 1680 (км) 2. Запись решения по действиям с вопросами: 1) Сколько километров проехал турист на поезде? 56 ∙ 6 = 336 (км) 2) Сколько километров осталось проехать туристу? 336 ∙ 4= 1344 (км) 3) Сколько километров турист должен был проехать? 336 + 1344= 1680 (км) 3. Запись решения в виде выражения. Запись решения в этой форме осуществляется поэтапно. Сначала записываются отдельные шаги в соответствии с планом, затем составляется выражение и находится его значение. Так как обычно это значение записывают, поставив после числового выражения знак равенства, то запись становится числовым равенством, в левой части которого-выражение, составленное по условию задачи, а в правой - его значение, оно-то и позволяет сделать вывод о выполнении требований задачи. Так, для рассматриваемой задачи эта форма записи имеет вид: 56 • 6 (км) - расстояние, которое проехал турист на поезде за 6 ч 56 ∙ 6 ∙ 4 (км) - расстояние, которое осталось проехать туристу 56-6 + 56-6-4 (км) - путь, который должен проехать турист 56 ∙ 6 + 56 ∙ 6 ∙ 4= 1680 (км) Пояснения к действиям можно не записывать, а давать их в устной форме. Тогда запись решения задачи примет вид: 56 ∙ 6 + 56 ∙ 6 ∙ 4= 1680 (км) Геометрические фигуры в пространстве С пространственными геометрическими фигурами (куб, шар, параллелепипед и др.) дети знакомятся в практической деятельности (при конструировании, во время игры) гораздо раньше, чем с плоскими фигурами. Особенности мышления младших дошкольников определяют выбор наглядного материала. В этом возрасте важно, чтобы изучаемый объект был крупный, яркий, чтобы им можно было выполнять действия (поиграть). Обследование идет на сенсорной основе, поэтому с моделями объемных фигур детям знакомиться легче. Кубики, шарики, бруски и др. входят в игру детей одновременно с первыми игрушками. Обычно математические названия им не даются, но идет знакомство с различными объемными формами, а в речь вводятся только некоторые термины. Основными фигурами в пространстве считаются: точка, прямая, плоскость. На каждой плоскости выполняются все утверждения планиметрии. В стереометрии, так же как в планиметрии, вводится ряд аксиом, которые изучаются в школьном курсе геометрии. Объемные геометрические фигуры называют геометрическими телами. В пространстве выделяют многогранники (призма, пирамида и др.) и тела вращения (шар, конус, цилиндр и др.). Многогранники Многогранник – это ограниченное тело, поверхность которого состоит из конечного числа многоугольников. Эти многоугольники называются гранями, их стороны – ребрами, а вершины – вершинами многогранника. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани (рис. 70). Поможем написать работу на аналогичную тему Выпуклый многогранник невыпуклый многогранник
Рис. 70 Всего существует 5 правильных многогранников, в отличие от правильных многоугольников, которых бесконечно много. Это обусловлено двумя причинами: 1. Сумма плоских углов, сходящихся в одной вершине, должна быть меньше 360º. 2. Сумма ребер, сходящихся в одной вершине должна быть не меньше 3. Правильными выпуклыми многогранниками являются: тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр (рис. 71). Первая часть в этих названиях в переводе с греческого обозначает количество граней (тетра – 4, гекса – 6, окта – 8, додека – 12, икоса – 20), а вторая – слово «грань» («хедрон»).  Одним из самых знакомых детям правильных многогранников является куб (гексаэдр). Куб – это правильный многогранник, гранями которого являются равные квадраты, а в каждой вершине сходятся по 3 ребра. Среди выпуклых многогранников выделяют призмы и пирамиды. Детские конструкторы содержат различные виды призм (рис. 72), а также другие многогранники.  треугольная прямоугольный куб шестиугольная призма параллелепипед призма Рис. 72 Призма – это многогранник, состоящий из двух плоских многоугольников (оснований), лежащих в разных плоскостях, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (рис. 73). В зависимости от количества углов многоугольника, являющегося основанием, призмы бывают: треугольные (рис. 74), четырехугольные и другие. 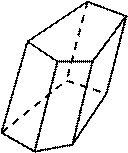 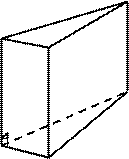 Рис. 73 Рис. 74 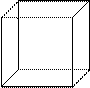  Рис. 75 Рис. 76 Частным случаем призмы являются прямоугольный параллелепипед и куб. Модели этих фигур используются маленькими детьми в строительных играх. Прямоугольный параллелепипед – это параллелепипед, все грани которого прямоугольники (рис. 75). Куб – это прямоугольный параллелепипед с равными ребрами (или все грани которого являются квадратами) (рис. 76). Дошкольники, изучая куб, могут отметить, что его поверхность состоит из шести квадратов, что у него 8 вершин. Свойства куба осваиваются ими, например, при выполнении такого задания: «Обклей кубик цветной бумагой. Что для этого нужно?» (вырезать 6 одинаковых квадратов). Прямоугольный параллелепипед в детском саду часто называют «кирпичиком» или «бруском», что допустимо в предматематической подготовке. Эти слова являются предэталонными названиями геометрических фигур, так же как «кубик», «крыша» (треугольная призма), «столбик» (цилиндр) и др. Младшим школьникам можно предложить задание: «Вырежи выкройку для коробки. Какую форму имеет каждую часть?» Таким образом, дети выясняют, что гранями прямоугольного параллелепипеда являются прямоугольники, не формулируя этого явно. Пирамида – многогранник, состоящий из плоского многоугольника (основания), точки, не лежащей в плоскости основания (вершины), и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 77). Отрезки, соединяющие вершины пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Все боковые грани – треугольники. В зависимости от числа углов многоугольника, являющегося основанием, пирамиды бывают: треугольные (рис. 77а), четырехугольные (рис. 77б), пятиугольные и другие пирамиды. 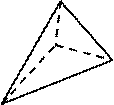             а) б) в) Рис. 77 Любая грань треугольной пирамиды может служить ее основанием. Это же название носит и правильный многогранник, тетраэдр, гранями которого являются равные равносторонние треугольники. Форму тетраэдра имеет пакет молока (старой упаковки), а египетские пирамиды имеют форму четырехугольной правильной пирамиды. Дошкольники называют «пирамидкой» совсем другую модель – игрушку из колец разной величины, которая имеет форму конуса. Эта ситуация может вызвать затруднения в запоминании и правильном применении геометрических терминов у детей. Данная проблема преодолевается при своевременном грамотном объяснении и разделении названий игрушек от названий их формы, эталонами для определения которой служат геометрические фигуры. Тела вращения  Изучая форму окружающих предметов, дошкольники сталкиваются с телами вращения (рис. 78).
цилиндр конус шар Рис. 78 Эти фигуры называются телами вращения, так как они могут быть получены путем вращения некоторых плоских геометрических фигур. Цилиндр – это тело вращения, которое может быть получено путем вращения прямоугольника вокруг одной из его сторон, как оси (рис. 79). Конус – это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его катетов, как оси (рис. 80). Шар – это тело вращения, которое может быть получено путем вращения половины круга его диаметра, как оси (рис. 81). Определения этих фигур из курса геометрии средней школы: Цилиндр – тело, которое состоит из двух кругов (оснований), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Конус – тело, которое состоит из круга (основания), точки (вершины), не лежащей в плоскости этого круга, и всех отрезков, соединяющих вершину конуса с точками основания. Шар – тело, которое состоит из всех точек пространства, находящихся на расстоянии не более заданного (радиуса) от данной точки (центра).
Рис. 79 Рис. 80 Рис. 81 Дошкольники не знакомятся с этими формулировками, но могут различать и узнавать объемные тела, а если провести специальную работу, и правильно называть их. Дети усваивают свойства этих фигур в сравнении с другими. Например, во время игры «Катится – не катится» они выясняют, что: «Цилиндр, стоящий на основании, устойчив, как куб, но если его положить – катится, как шар». Обследование поверхности дает знание того, что основанием цилиндра и конуса является круг. Рисование объемных предметов разной формы на плоскости учит детей сравнивать, проводить аналогию, моделировать, трансформировать пространство на плоскости. Например, в процессе обсуждения таких вопросов: «Какой формы мяч? Какую фигуру надо нарисовать, чтобы изобразить мяч?» Знакомство с объемными фигурами расширяет знания детей об окружающем мире, закладывает основы для изучения геометрии в школе, обогащает их речь, формирует навыки обследования, развивает мышление. ТЕМА. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ И ИХ СВОЙСТВА Геометрическую фигуру определяют как любое множество точек. Отрезок, прямая, круг, шар - геометрические фигуры. Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской. Например, отрезок, прямоугольник - это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида. Так как понятие геометрической фигуры определено через понятие множества, то можно говорить о том, что одна фигура включена в другую (или содержится в другой), можно рассматривать объединение, пересечение и разность фигур. Например, объединением двух лучей АВ и МК (рис. 1) является прямая КВ, а их пересечение есть отрезок АМ. К А М В
Рис. 1 Различают выпуклые и невыпуклые фигуры. Фигура называется выпуклой, если она вместе с любыми двумя своими точками содержит также соединяющий их отрезок. Фигура F1, изображенная на рисунке 2, выпуклая, а фигура F2 - невыпуклая.
F2 X Y 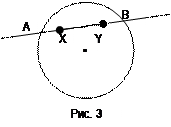 Выпуклыми фигурами являются плоскость, прямая, луч, отрезок, точка. Нетрудно убедиться в том, что выпуклой фигурой является круг (рис. 3). Если продолжить отрезок XY до пересечения с окружностью, то получим хорду АВ. Так как хорда содержится в круге, то отрезок XY тоже содержится в круге и, значит, круг - выпуклая фигура.Для многоугольников известно другое определение: многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Так как равносильность этого определения и данного выше для многоугольника доказана, то можно пользоваться и тем, и другим. Основываясь на этих понятиях, рассмотрим другие геометрические фигуры, изучаемые в школьном курсе планиметрии. Рассмотрим их определения и основные свойства, принимая их без доказательства. Знание этого материала и умение применять к решению несложных геометрических задач является той основой, на которой можно строить методику обучения младших школьников элементам геометрии. Углы Напомним, что угол - это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало - его вершиной. Угол обозначают по-разному: указывают либо его вершину, либо его стороны, либо три точки: вершину и две точки на сторонах угла: ÐА, Ð(k,l), ÐАВС. Угол называется развернутым, если его стороны лежат на одной прямой. Угол, составляющий половину развернутого угла, называется прямым. Угол, меньший прямого, называется острым. Угол, больший прямого, но меньший развернутого, называется тупым. Кроме понятия угла, данного выше, в геометрии рассматривают понятие плоского угла. Плоский угол - это часть плоскости, ограниченная двумя различными лучами, исходящими из одной точки. Углы, которые рассматривают в планиметрии, не превосходят развернутого. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми. Сумма смежных углов равна 180°. Справедливость этого свойства вытекает из определения смежных углов. 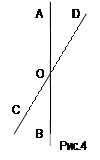 Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Углы АОВ и СОВ, а также углы АОС и D0В - вертикальные (рис. 4).Вертикальные углы равны. Справедливость этого свойства вытекает из определения вертикальных углов и свойства смежных углов. Треугольники Треугольник - одна из простейших геометрических фигур. Но его изучение породило целую науку - тригонометрию, которая возникла из практических потребностей при измерении земельных участков, составлении карт местности, конструировании различных механизмов. Первые упоминания о треугольнике и его свойствах содержатся в египетских папирусах. Например, в них предлагается находить площадь равнобедренного треугольника как произведение половины основания на боковую сторону, хотя для любого равнобедренного треугольника с малым углом при вершине, противоположной основанию, такой способ дает приближенное значение площади. Многие свойства треугольников были открыты и доказаны математиками Древней Греции. Среди них - знаменитая теорема Пифагора. Рассмотрим основные понятия, связанные с треугольником. Треугольником называется геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков. Любой треугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из треугольника и его внутренней области, также называют треугольником (или плоским треугольником). В любом треугольнике выделяют следующие элементы: стороны, углы, высоты, биссектрисы, медианы, средние линии. Углом треугольника АВС при вершине А называется угол, образованный полупрямыми АВ и АС. Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противолежащую сторону. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне. Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон. На практике и в теоретических построениях часто пользуются признаками равенства треугольников, обеспечивающими более быстрое решение вопроса об отношениях между ними. Таких признаков три. 1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. 3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника. Равнобедренные треугольники обладают рядом свойств, например: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. Отметим еще несколько важных свойств треугольников. 1. Сумма углов треугольника равна 180°.Из этого свойства следует, что в любом треугольнике хотя бы два угла острые. 2. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине. 3. В любом треугольнике каждая сторона меньше суммы двух других сторон. Для прямоугольного треугольника с углом 30° справедливо следующее свойство: катет, противолежащий этому углу, равен половине гипотенузы. Для прямоугольного треугольника верна теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Четырехугольники Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки - его сторонами. Любой четырехугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из четырехугольника и его внутренней области, также называют четырехугольником (или плоским четырехугольником). Вершины четырехугольника называют соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями. Стороны четырехугольника, исходящие из одной вершины, называются соседними. Стороны, не имеющие общего конца, называются противолежащими. У четырехугольника АВС D (рис. 5) вершины А и В - соседние, а вершины А и С - противолежащие; стороны АВ и ВС - соседние, ВС и А D -противолежащие; отрезки АС и В D -диагонали данного четырехугольника. 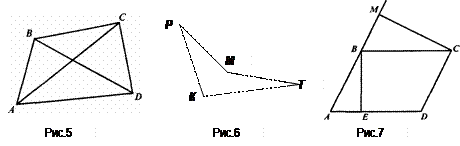 Четырехугольники бывают выпуклые и невыпуклые. Так, четырехугольник АВС D (рис. 5) - выпуклый, а четырехугольник КРМТ (рис. 6) невыпуклый. Среди выпуклых четырехугольников выделяют параллелограммы и трапеции.Многоугольники Обобщением понятия треугольника и четырехугольника является понятие многоугольника. Определяется оно через понятие ломаной. Ломаной А1А2А3…А n называется фигура, которая состоит из точек А1,А2,А3,…,А n , и соединяющих их отрезков А1А2, А2А3, ... А n-1 А n . Точки А1,А2,А3,…,Аn называются вершинами ломаной, а отрезки А1А2, А2А3, ... Аn-1Аn - ее звеньями. Если ломаная не имеет самопересечений, то она называется простой. Если ее концы совпадают, то она называется замкнутой. О ломаных, изображенных на рисунке 8, можно сказать, что: А1,А2,А3,А4,А5,А6 -простая; А1,А2,А3 - простая замкнутая; А1,А2,А3,А4 - замкнутая ломаная, но она не является простой, так как имеет самопересечение. Длиной ломаной называется сумма длин ее звеньев.
 Известно, что длина ломаной не меньше длины отрезка, соединяющего ее концы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расстояние
