Главная страница
Навигация по странице:

  • Закрытые интервалы Середина интервала, (х) Число студентов, % к итогу, (f)

  • Всего – – 100

  • Затраты времени на дорогу до института, час Середина интервала, (х)

  • Всего - 100 133,5

  • Всего - 100 2,53613

  • S(Me-1)

    		•

    статистика задачи. Документ Microsoft Word (2). Задача Имеются следующие данные о размере прибыли предприятий по регионам Предприятия с прибылью


    Скачать 58.15 Kb.
    НазваниеЗадача Имеются следующие данные о размере прибыли предприятий по регионам Предприятия с прибылью
    Анкорстатистика задачи
    Дата05.05.2021
    Размер58.15 Kb.
    Формат файлаdocx
    Имя файлаДокумент Microsoft Word (2).docx
    ТипЗадача
    #201909

    Задача 1.2. Имеются следующие данные о размере прибыли предприятий по

    регионам:

    Предприятия с прибылью,

    млн. руб.
    Количество предприятий

    в 1-м регионе
    во 2-м регионе
    в 3-м регионе

    200 – 300
    10
    20
    5

    300 – 400
    15
    25
    10

    400 – 500
    20
    15
    15

    500 - 600
    5
    10
    11

    Определите средний размер прибыли, приходящийся на одно предприятие:

    а) по каждому региону; б) по трем регионам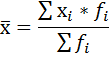

    Формула средней арифметической взвешенной

    а) Для региона 1:

    Прибыль, млн. руб
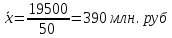    Количество предприятий (fi)
    Середина интервала (xi)
    Xi*fi

    200 -300
    10
    250
    2500

    300 – 400
    15
    350
    5250

    400 – 500
    20
    450
    9000

    500 - 600
    5
    550
    2750

    Итого
    50
    -
    19500

    – средний размер прибыли, приходящийся в первом регионе на одно предприятие

    Для региона 2:

    Прибыль, млн. руб
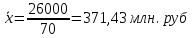    Количество предприятий (fi)
    Середина интервала (xi)
    Xi*fi

    200 -300
    20
    250
    5000

    300 – 400
    25
    350
    8750

    400 – 500
    15
    450
    6750

    500 - 600
    10
    550
    5500

    Итого
    70
    -
    26000

    - средний размер прибыли, приходящийся во втором регионе на одно предприятие

    Для региона 3:

    Прибыль, млн. руб
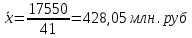    Количество предприятий (fi)
    Середина интервала (xi)
    Xi*fi

    200 -300
    5
    250
    1250

    300 – 400
    10
    350
    3500

    400 – 500
    15
    450
    6750

    500 - 600
    11
    550
    6050

    Итого
    41
    -
    17550

    - средний размер прибыли, приходящийся в третьем регионе на одно предприятие

    б) Для всех регионов

    Прибыль, млн. руб
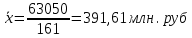    Количество предприятий (fi)
    Середина интервала (xi)
    Xi*fi

    200 -300
    35
    250
    8750

    300 – 400
    50
    350
    17500

    400 – 500
    50
    450
    22500

    500 - 600
    26
    550
    14300

    Итого
    161
    -
    63050

    - средний размер прибыли, приходящийся во всех трех регионах на одно предприятие

    Задача 2.2. Имеются следующие данные выборочного обследования студентов ВУЗа:

    Затраты времени на дорогу в ВУЗ, ч
    Число студентов, % к итогу

    До 0,2
    7

    0,2-0,5
    18

    0,5-0,8
    37

    0,8-1,1
    32

    Свыше 1,1
    6

    Итого
    100

    Рассчитайте средние затраты времени на дорогу в ВУЗ, а также абсолютные и относительные показатели вариации.

    Средние затраты на дорогу:

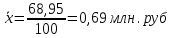    Затраты времени на дорогу в ВУЗ, ч
    Число студентов, % к итогу
    Середина интервала (xi)
    Xi*fi

    До 0,2
    7
    0,1
    0,7

    0,2-0,5
    18
    0,35
    6,3

    0,5-0,8
    37
    0,65
    24,05

    0,8-1,1
    32
    0,95
    30,4

    Свыше 1,1
    6
    1,25
    7,5

    Итого
    100



    68,95

    - средние затраты времени на дорогу в ВУЗ

    Найдём абсолютные показатели вариации:

    1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:



    Размах вариации затрат времени на дорогу до института равен 2,5 часа.

    2) Средние затраты времени определим по формуле средней арифметической взвешенной.

    Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.

    Среднее значение первого интервала будет равно:



    Занесём результаты вычислений в таблицу:

    Затраты времени на дорогу до института, час
    Закрытые интервалы
    Середина интервала, (х)
    Число студентов, % к итогу, (f)
    хf

    До 0,5
    0 – 0,5
    0,25
    7
    1,75

    0,5 – 1,0
    0,5 – 1,0
    0,75
    18
    13,5

    1,0 – 1,5
    1,0 – 1,5
    1,25
    32
    40

    1,5 – 2,0
    1,5 – 2,0
    1,75
    37
    64,75

    Свыше 2,0
    2,0 – 2,5
    2,25
    6
    13,5

    Всего___-__100___133,5'>Всего__–_–_100'>Всего
    –
    –
    100
    133,5



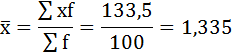    3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней: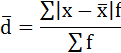



    Затраты времени на дорогу до института, час
    Середина интервала, (х)
    Число студентов, % к итогу, (f)
    хf




     До 0,5
    0,25
     7
     1,75
     1,085
     7,595

     0,5 – 1,0
    0,75 
    18 
     13,5
     0,585
     10,53

    1,0 – 1,5 
    1,25 
    32 
     40
     0,085
     2,72

     1,5 – 2,0
    1,75 
    37 
     64,75
     0,415
    15,355 

     Свыше 2,0
    2,25 
     6
     13,5
     0,915
     4,49

     Всего
     -
    100 
     133,5
    - 
     41,69

     

    Среднее линейное отклонение затрат времени составляет 0,4169 часа.

    4) Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.

    Расчёт дисперсии в интервальных рядах распределения производится по формуле: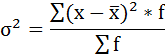



    Построим вспомогательную таблицу:

    Затраты времени на дорогу до института, час
    Середина интервала, (х)
    Число студентов, % к итогу, (f)




     До 0,5
    0,25
     7
    1,17723
    8,24058

     0,5 – 1,0
    0,75 
    18 
    0,34223
    6,16005

    1,0 – 1,5 
    1,25 
    32 
    0,00722
    0,2312

     1,5 – 2,0
    1,75 
    37 
    0,17223
    6,37233

     Свыше 2,0
    2,25 
     6
    0,83723
    5,02335

     Всего
     -
    100 
    2,53613
    26,0275



     5) Среднее квадратическое отклонение затрат времени определяется как корень квадратный из дисперсии:

     

    Найдём относительные показатели вариации:

    6) Коэффициент вариации - это отношение среднего квадратического отклонения к средней арифметической: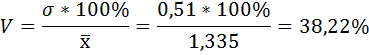



    По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значения признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.

    Поскольку  V > 33%, следовательно, вариация значительная, а совокупность  не однородна.

    7) Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней и определяется по формуле: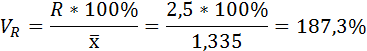



    8) Относительное линейное отклонение: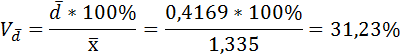



    Вариант2. По данным о численности жителей двух крупнейших городов

    России(тыс. чел) определить индексы сравнения и динамики.

    Город Год
    2004
    2005

    Москва
    10391
    10407

    Санкт-Петербург
    4624
    4600

    Индекс динамики характеризует изменение какого-либо явления во времени. Он представляет собой отношение значений одной и той же абсолютной величины в разные периоды времени. Данный индекс определяется по формуле:

    Iд=x2005/x2004

    Критериальным значением индекса динамики служит единица, то есть если >1, то имеет место рост явления во времени; если =1 - стабильность; если <1 - наблюдается спад явления. Применяя формулу, имеем:

    Для Москвы: = 10407/10391 = 1,00154 ненамного больше 1 - можно говорить о небольшом росте численности населения в Москве.

    Для Санкт-Петербурга: = 4600/4624 = 0,99481 < 1 - наблюдается уменьшение численности населения в Санкт-Петербурге.

    Индекс сравнения - это отношение значений одной и той же величины в одном периоде или моменте времени, но для разных объектов или территорий. Он определяется по формуле:

    Iср=xА/xБ

    Применяя формулу и принимая за объекты А и Б, соответственно, численность населения Москвы и Санкт-Петербурга, найдем индекс сравнения: = 10407/4600 = 2,26, то есть населения в Москве в 2005 году в 2,26 раза больше, чем в Санкт-Петербурге.

    В 2004 году = 10391/4624 = 2,25, то есть населения в Москве было в 2,25 раза больше, чем в Санкт-Петербурге.

    Найдем индекс сравнения для Санкт-Петербурга и Новосибирска: = 4600/1406 = 3,27, то есть населения в Санкт-Петербурге в 2005 году в 3,27раза больше, чем в Новосибирске. В 2004 году = 4624/1413 = 3,27, то есть населения в Санкт-Петербурге было также в 3,27 раза больше, чем в Новосибирске.

    По имеющимся в следующей таблице данным по группе из20 студентов

    заочного отделения необходимо:

    1) построить интервальный ряд распределения признака и его график;

    2) рассчитать модальное, медианное и среднее значение, установить его

    типичность с помощью коэффициентов вариации;

    3) проверить распределение на нормальность с помощью коэффициентов

    асимметрии и эксцесса.

     
    вес, кг

    1
    45

    2
    61

    3
    56

    4
    48

    5
    54

    6
    58

    7
    51

    8
    62

    9
    70

    10
    72

    11
    73

    12
    64

    13
    73

    14
    68

    15
    81

    16
    84

    17
    76

    18
    90

    19
    68

    20
    95

    1) По формуле Стерджесса совокупность надо разделить на 1 + 3,322 lg 20 = 5 групп.

    Максимальный возраст – 95, минимальный – 45

    №
    Вес, кг
    Частота

    1
    45-55
    4

    2
    56-65
    5

    3
    66-75
    6

    4
    76-85
    3

    5
    86-95
    2




    Всего
    20

    .

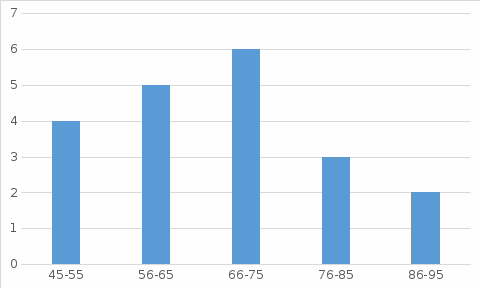    Определим модальное и медианное значение месячного товарооборота.

    В интервальных рядах распределения с равными интервалами мода определяется по формуле: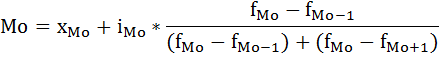



    xMo – начальное значение интервала, содержащего моду;

    iMo – величина модального интервала,

    fMo – частота модального интервала,

    f(Mo-1) – частота интервала, предшествующего модальному,

    f(Mo+1) – частота интервала, следующего за модальным.

    Наибольшее количество человек (6) имеют вес от 66 до 75 кг. Следовательно, этот интервал является модальным интервалом ряда распределения. Введём следующие обозначения:

    xMo=66, iMo=10, fMo=6, f(Mo-1)=5, f(Mo+1)=3.

    Подставим эти значения в формулу моды и произведём вычисления:

    M0=66+10*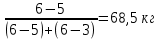

    Следовательно, наибольшее количество человек имеет вес 68,5 кг.

    Медиана интервального вариационного ряда распределения определяется по формуле: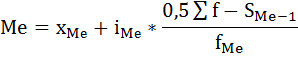



    где xMе – начальное значение интервала, содержащего медиану;
    iMе – величина медианного интервала;
    Σf – сумма частот ряда;
    S(Me-1) – сумма накопленных частот, предшествующих медианному интервалу;
    fMe – частота медианного интервала.

    Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (15), соответствует интервалу 66 - 75. Это и есть медианный интервал, в котором находится медиана. Определим её значение по приведённой выше формуле, если:

    xMе=66, iMе=10, Σf=20, S(Me-1)=9, fMe=6:

    Ме=66+10*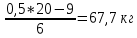

    Таким образом, половина людей вес менее 67,7 кг, а остальные – более 67,7 кг.

    Среднее значение:

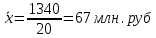    Вес, кг
    Количество человек (fi)
    Середина интервала (xi)
    Xi*fi

    45-55
    4
    50
    200

    56-65
    5
    60
    300

    66-75
    6
    70
    420

    76-85
    3
    80
    240

    86-95
    2
    90
    180

    Итого
    20



    1340


    написать администратору сайта