1. Теоретическая часть 21. Мультиколлинеарность факторов и ее влияние на надежность оценки объяснений вариации по отдельным факторам с помощью мнк
 Скачать 0.53 Mb.
|
|
Оглавление Оглавление 2 1.Теоретическая часть 3 Практическая часть 14 Литература 22 1.Теоретическая часть21.Мультиколлинеарность факторов и ее влияние на надежность оценки объяснений вариации по отдельным факторам с помощью МНК.Так как одним из условий построения уравнения множественной регрессии является независимость действия факторов, то коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Намного сложнее выявить так называемую мультиколлинеарность факторов, когда более чем два фактора связаны между собой нестрогой линейной зависимостью, то есть наибольшие трудности мы встречаем, когда необходимо выявить совокупное воздействие нескольких факторов друг на друга. Если при исследовании модели мы сталкиваемся в мультиколлинеарностью, это обозначает, что некоторые из включаемых в модель факторов всегда будут действовать вместе. И опять же возникает проблемы при оценке воздействия каждого фактора  на результат y в отдельности при неизменном значении прочих факторов, так как вариации мультиколлинеарных факторов перестают быть независимыми друг от друга. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.На практике о наличии мультиколлинеарности судят по матрице коэффициентов парной корреляции между факторами (почти такую мы уже рассматривали ранее, в нее не включается только корреляция с результативным признаком), точнее, по её определителю. Термин «коллинеарность» характеризует линейную связь между двумя объясняющими переменными. «Мультиколлинеарность» означает линейную связь между более чем двумя объясняющими переменными [1]. На практике всегда используется один термин - мультиколлинеарность. Термин «мультиколлинеарность» введен Рагнаром Фришем Рассматривают два вида мультиколлинеарности:
В задачах с реальными данными случай полной мультиколлинеарности встречается крайне редко. Вместо этого в прикладной области часто приходится иметь дело с частичной мультиколлинеарностью, которая характеризуется коэффициентами парной корреляции между регрессорами. В случае частичной мультиколлинеарности матрица  будет иметь полный ранг, но ее определитель будет близок к нулю. В этом случае формально можно получить оценки параметров модели и их точностные показатели, но все они будут неустойчивыми [1].Среди последствий частичной мультиколлинеарности можно выделить следующие:
Точные количественные критерии для обнаружения частичной мультиколлинеарности отсутствуют. В качестве признаков ее наличия чаще всего используют следующие:
Причины возникновения мультиколлинеарности:
Проблема мультиколлинеарности является обычной для регрессии временных рядов, т.е. когда данные состоят из ряда наблюдений в течение некоторого периода времени. Если две или более объясняющие переменные имеют ярко выраженной временной тренд, то они будут тесно коррелированы, и это может привести к мультиколлинеарности. Если среди парных коэффициентов корреляции независимых переменных существуют такие, значение которых приближается или равно множественному коэффициенту корреляции, то это говорит о возможности существования мультиколлинеарности [1]. Если в эконометрической модели получено малое значение параметра  при большом коэффициенте детерминации  и при этом  - критерий существенно отличается от нуля, то это говорит о наличии мультиколлинеарности.Методы исследования мультиколлинеарности
Стохастическая связь между переменными характеризуется величиной коэффициента корреляции между ними. Чем ближе по абсолютной величине значение коэффициента корреляции к единице, тем сильнее мультиколлинеарность. В общем случае, если при оценке уравнения регрессии несколько факторов оказались незначимыми, то нужно выяснить нет ли среди них коррелированных между собой. Для этого формируется матрица коэффициентов парной корреляции, которая является симметричной и называется корреляционной матрицей. Она имеет вид: 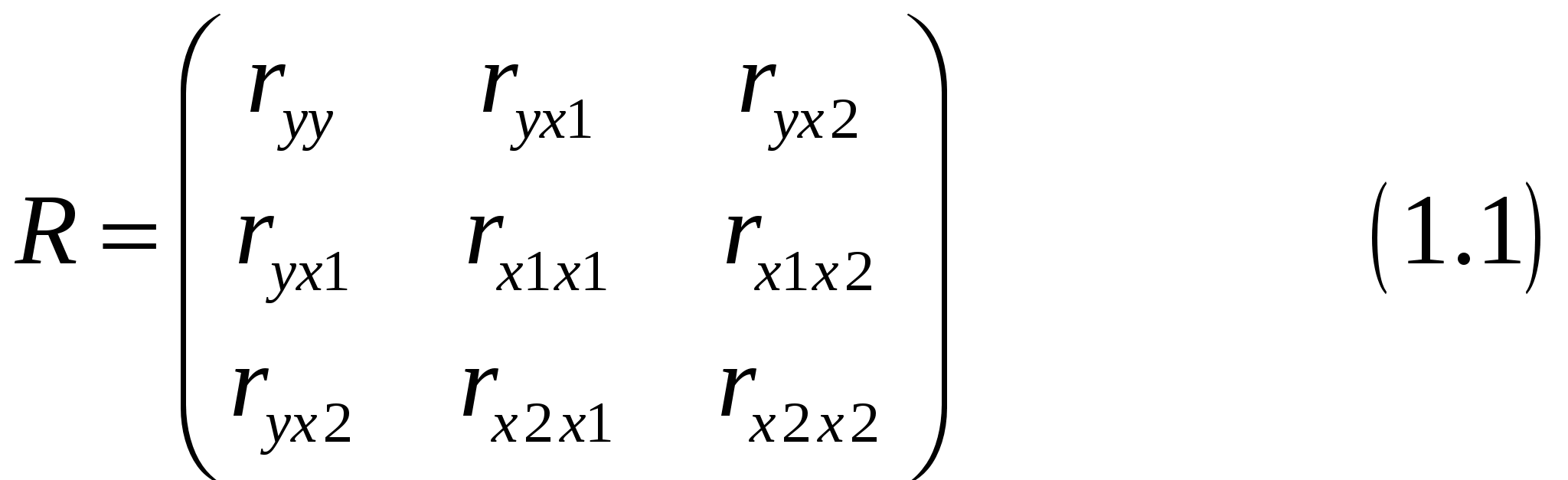 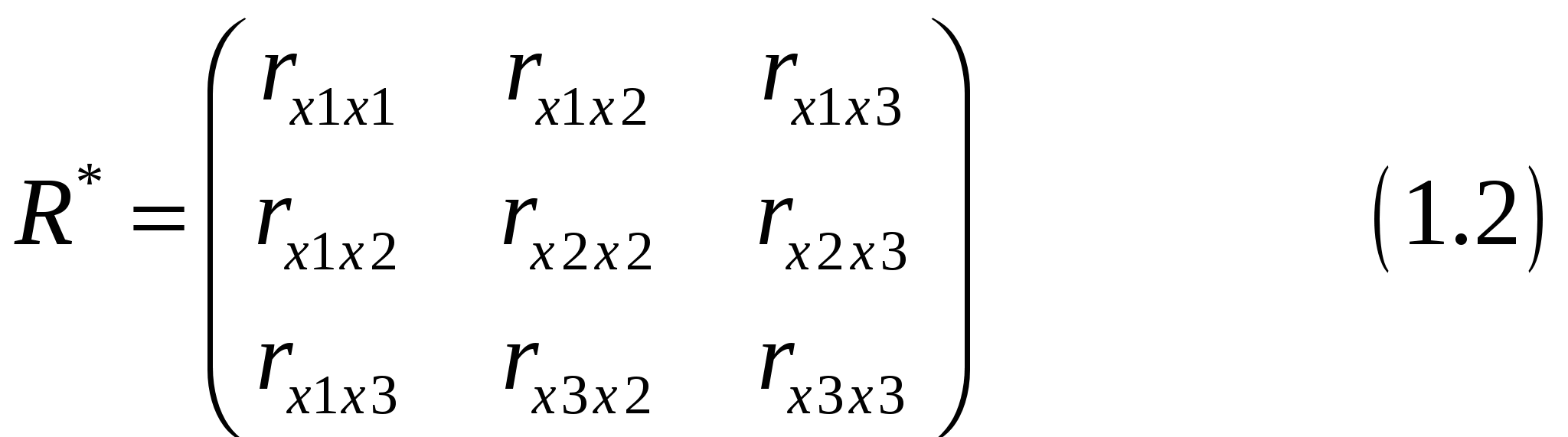 где 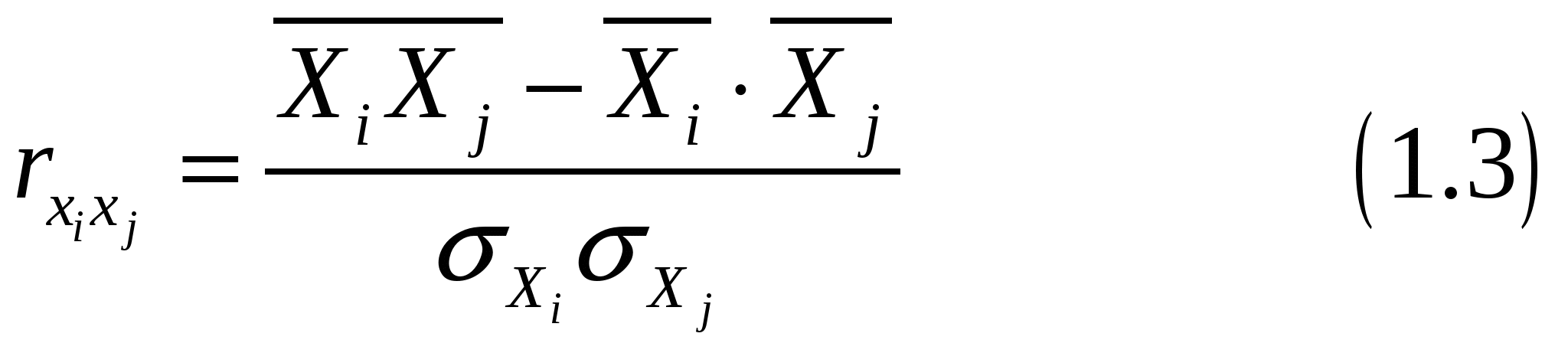 - коэффициенты парной корреляции между переменной  и одним из факторов,  - коэффициенты парной корреляции между факторами, которые вычисляются по формуле где  ,  ,  .Анализ корреляционной матрицы позволяет оценить, во-первых, степень влияния отдельных факторов на результативный показатель, во-вторых, взаимосвязь факторов между собой Если коэффициенты парной корреляции между некоторыми факторами близки к единице, это указывает на тесную взаимосвязь между ними, т.е. на наличие мультиколлинеарности. В этом случае один из факторов необходимо исключить из дальнейшего рассмотрения. Встает вопрос, какой именно. Это зависит от конкретной ситуации. Чаще всего для моделирования оставляют тот фактор, который с экономической точки зрения более весом для изучаемого процесса. Можно также оставить фактор, который имеет большее влияние на результативный показатель (т.е. коэффициент корреляции которого с результативным показателем больше). Такого рода анализ проводится для каждой пары факторов. Результатом анализа корреляционной матрицы является установление группы факторов, мало зависимых между собой - они и должны входить в модель.
Если в модели больше двух факторов, вопрос о мультиколлинеарности не может ограничиваться информацией, которую дает корреляционная матрица. Более широкая проверка предусматривает вычисление определителя матрицы  . Если  , то существует полная мультиколлинеарность. Если  , то мультиколлинеарности нет. Чем ближе  к нулю, тем увереннее можно утверждать о существовании между переменными мультиколлинеарности.
Для исследования общей мультиколлинеарности и мультиколлинеарности между отдельными факторами используется корреляционная матрица  .Для исследования общей мультиколлинеарности используется критерий 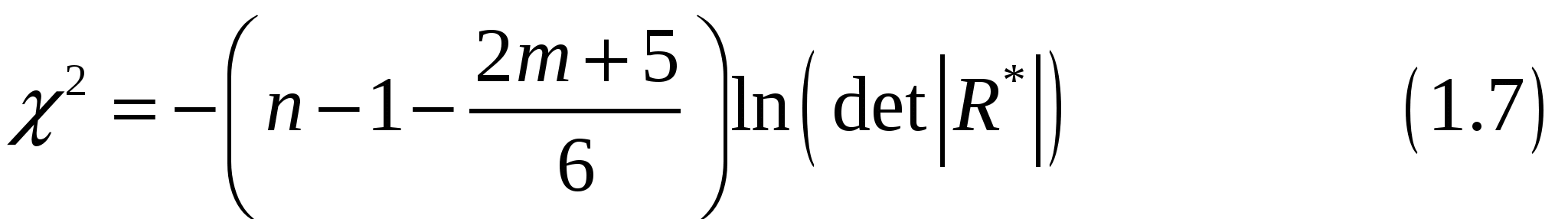 . Рассчитывается величина имеющая 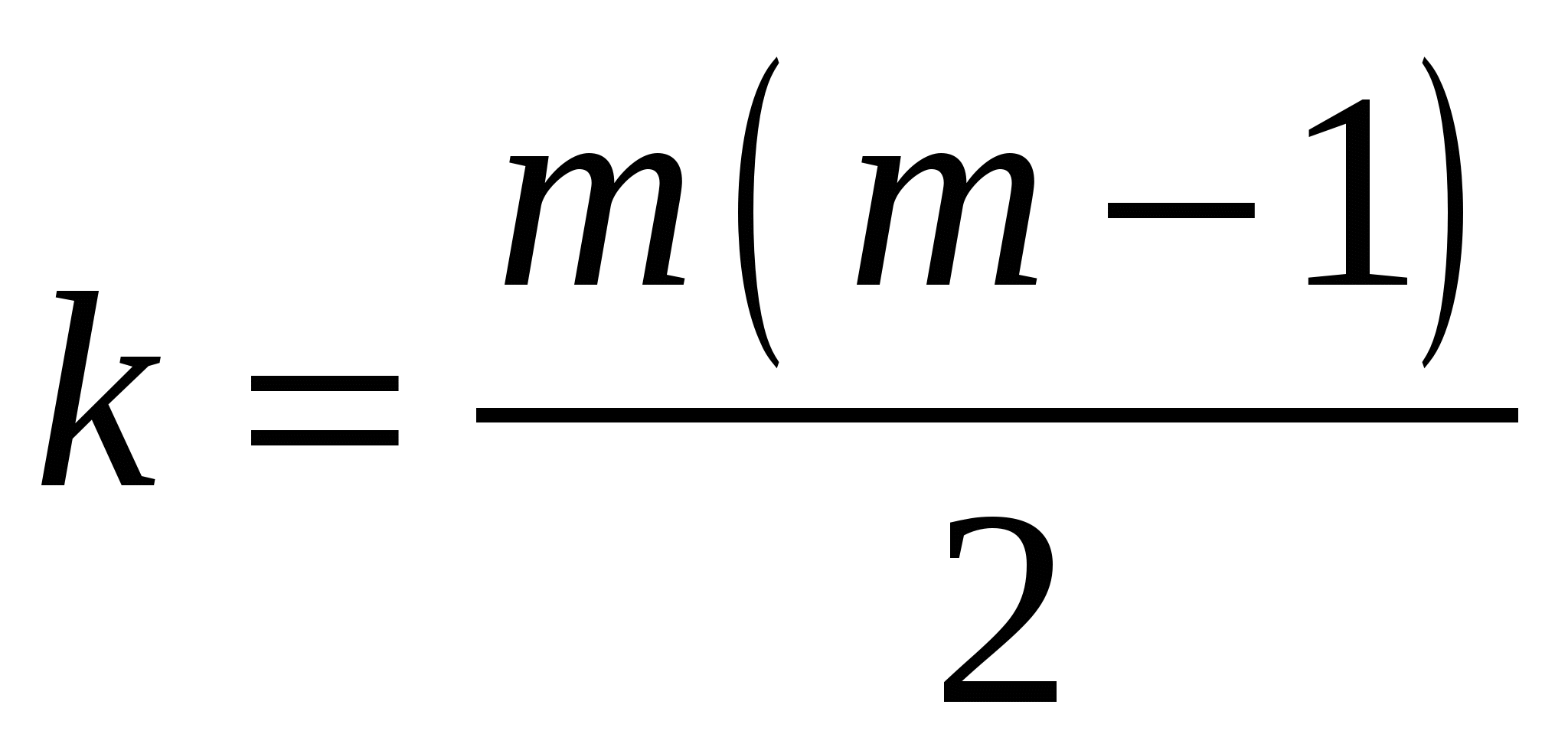- распределение с  степенями свободы.По данной надёжности 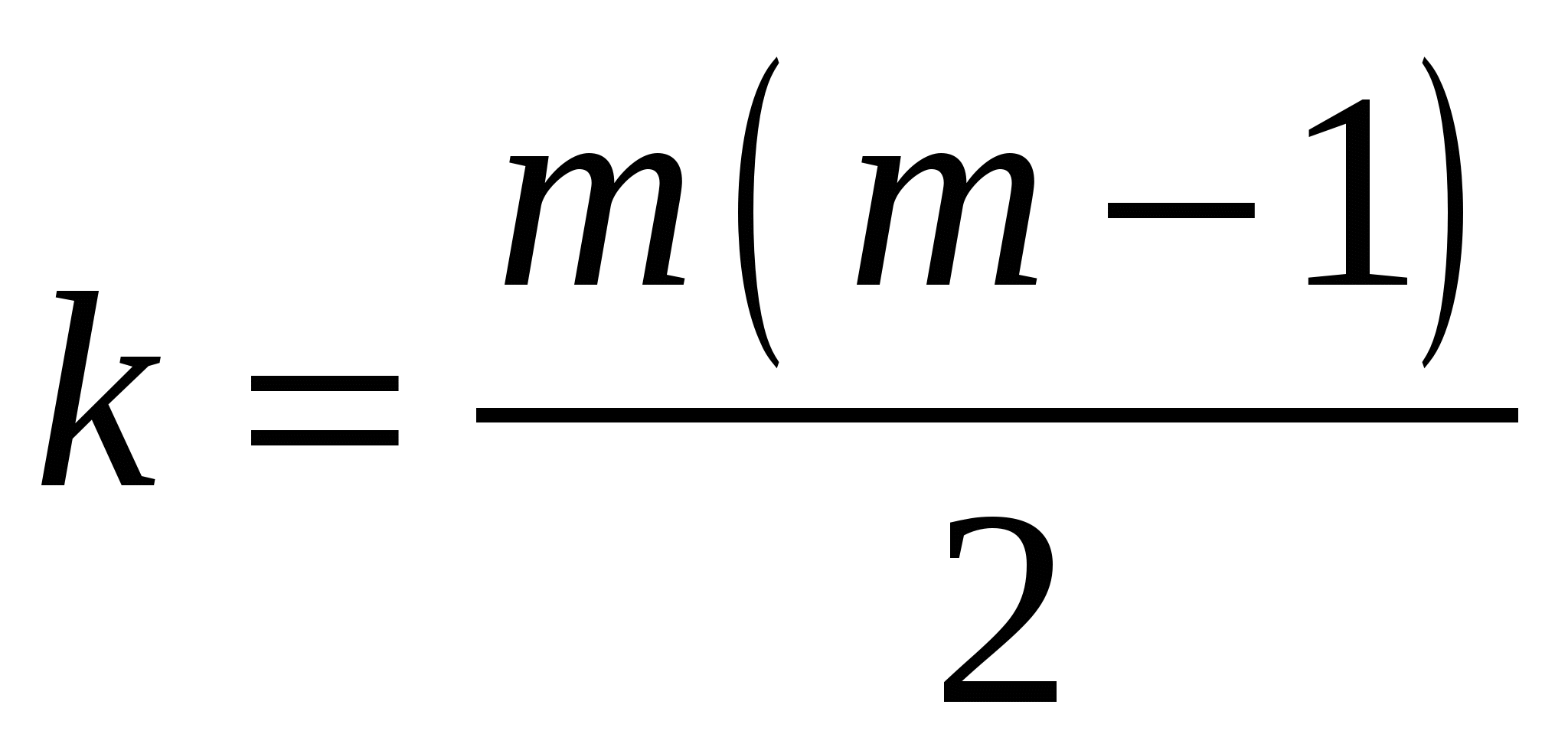 и числу степеней свободы находят табличное значение  . Если  , то можно считать, что мультиколлинеарность между объясняющими переменными отсутствует.Если  , то с заданной надёжностью можно считать, что между факторами существует общая мультиколлинеарность.Далее исследуется, какая объясняющая переменная порождает мультиколлинеарность, и решается вопрос об ее исключении из дальнейшего анализа. Для выяснения вопроса, между какими факторами существует мультиколлинеарность, используется 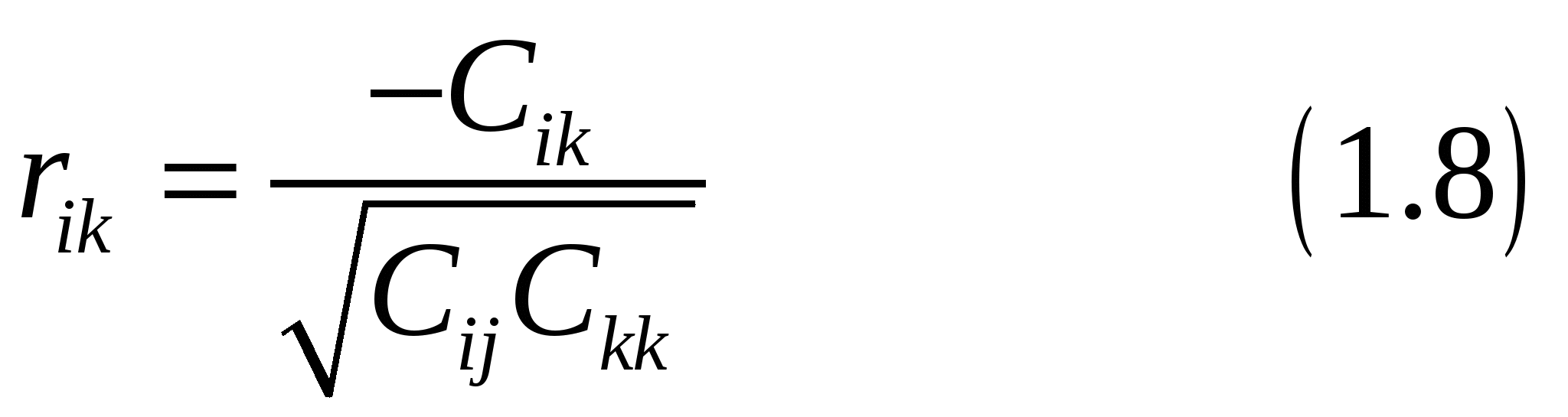статистика или  статистика. Для этой цели используют частные коэффициенты парной корреляции   между объясняющими переменными, которые вычисляют по формуле: где  - элементы обратной матрицы  .В качестве критерия используется величина 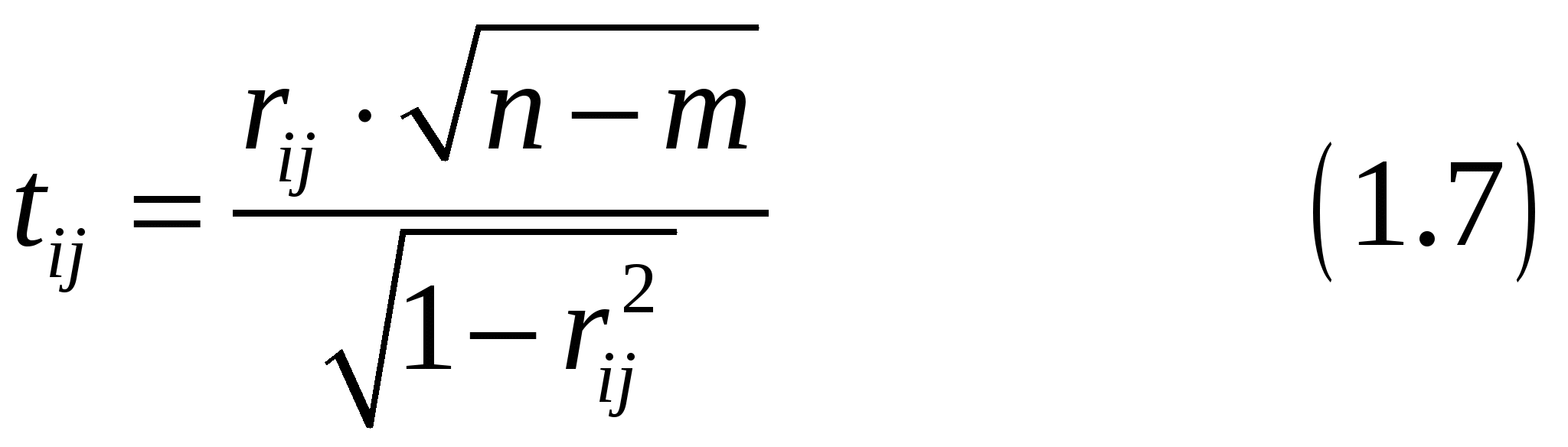 имеющая распределение Стьюдента с  степенями свободы.По таблицам Стьюдента находят критическое значение  . Сравнивают критическое значение  с расчетным  :
|
будет равен нулю. Полная мультиколлинеарность не позволяет однозначно оценить параметры исходной модели и разделить вклады регрессоров в выходную переменную по результатам наблюдений.
и 
, то между объясняющими переменными 
коллинеарности нет.
, то между объясняющими переменными