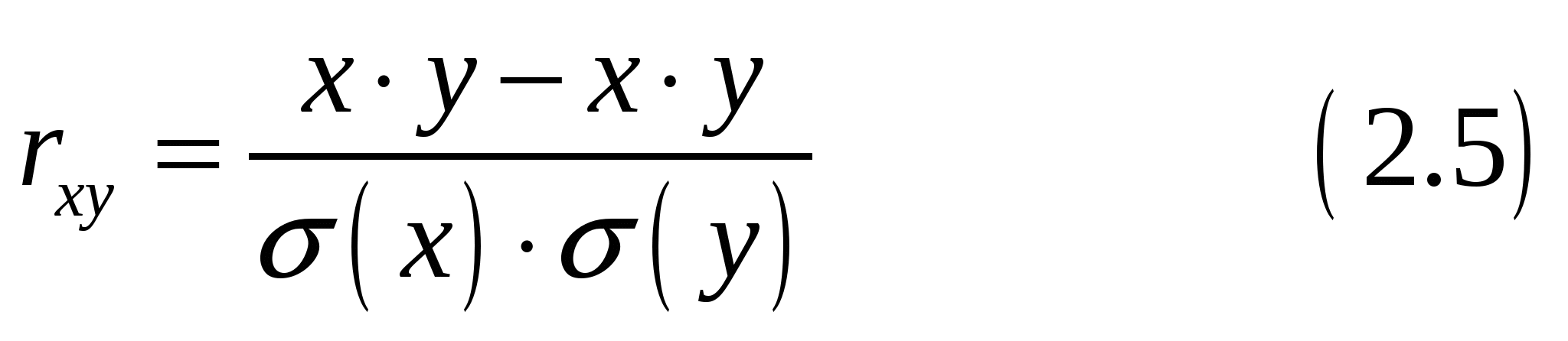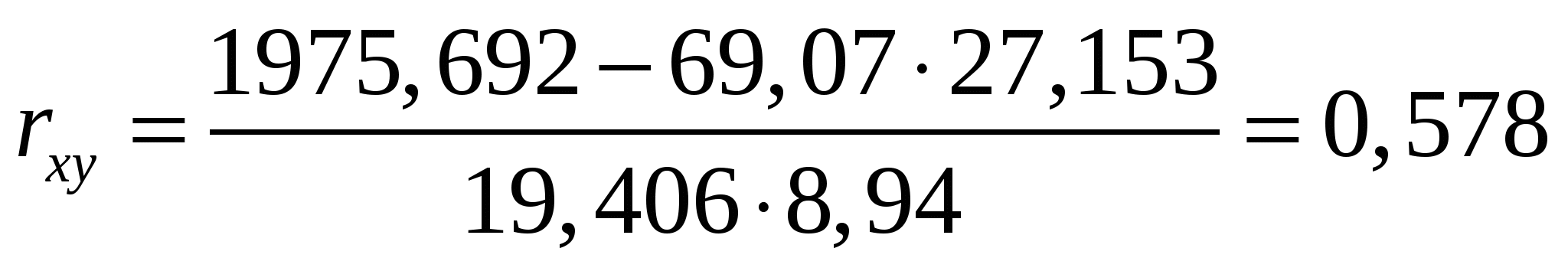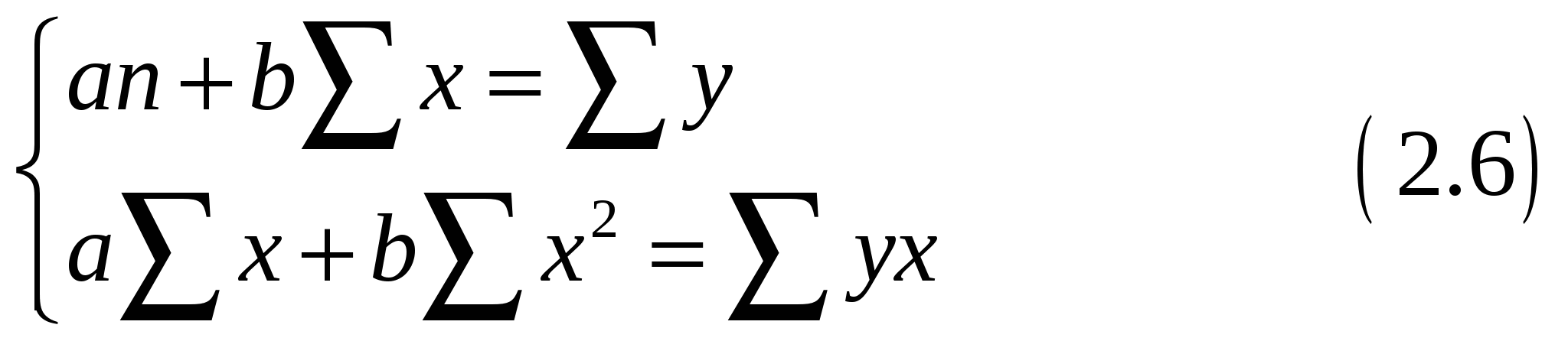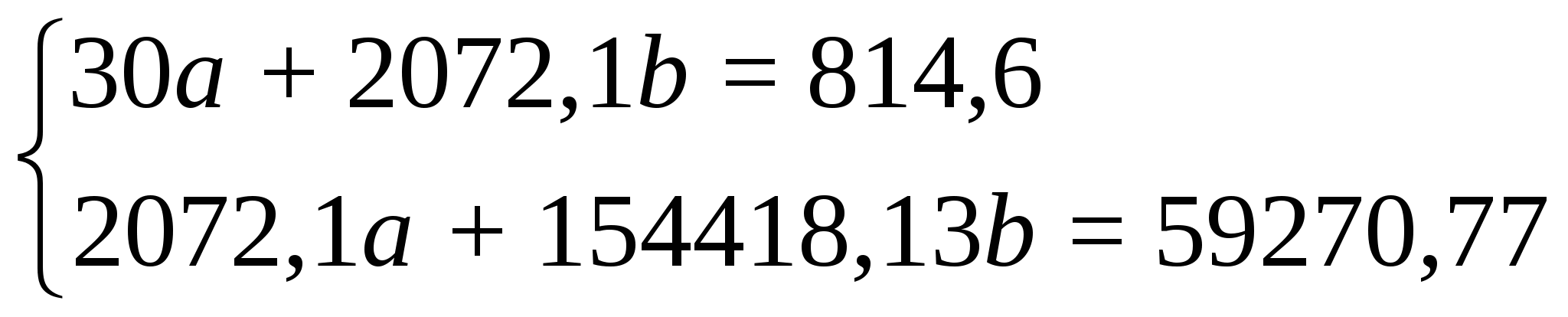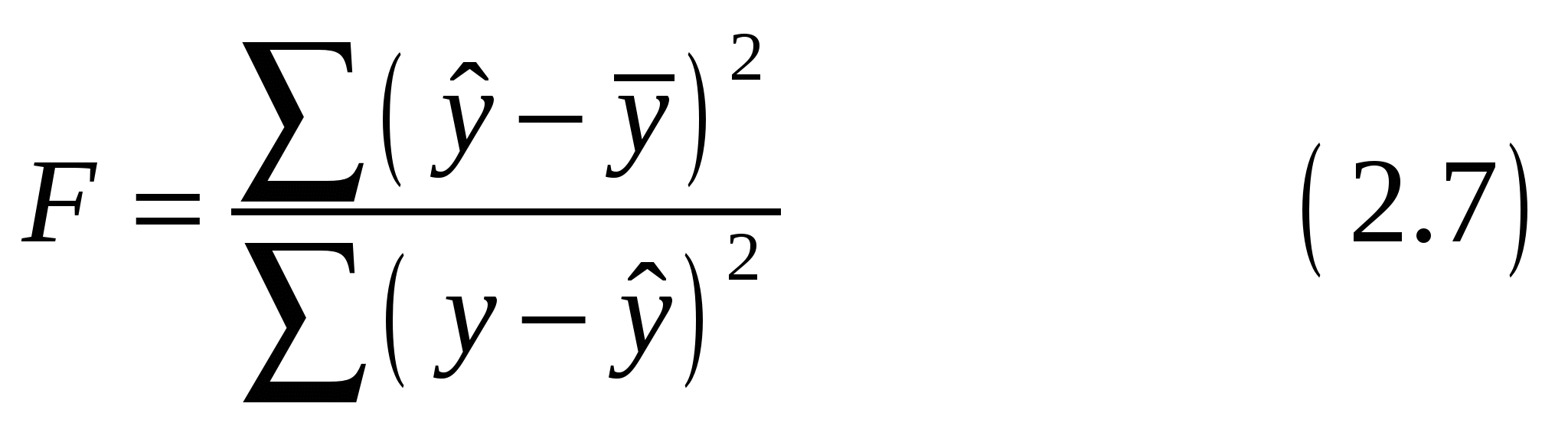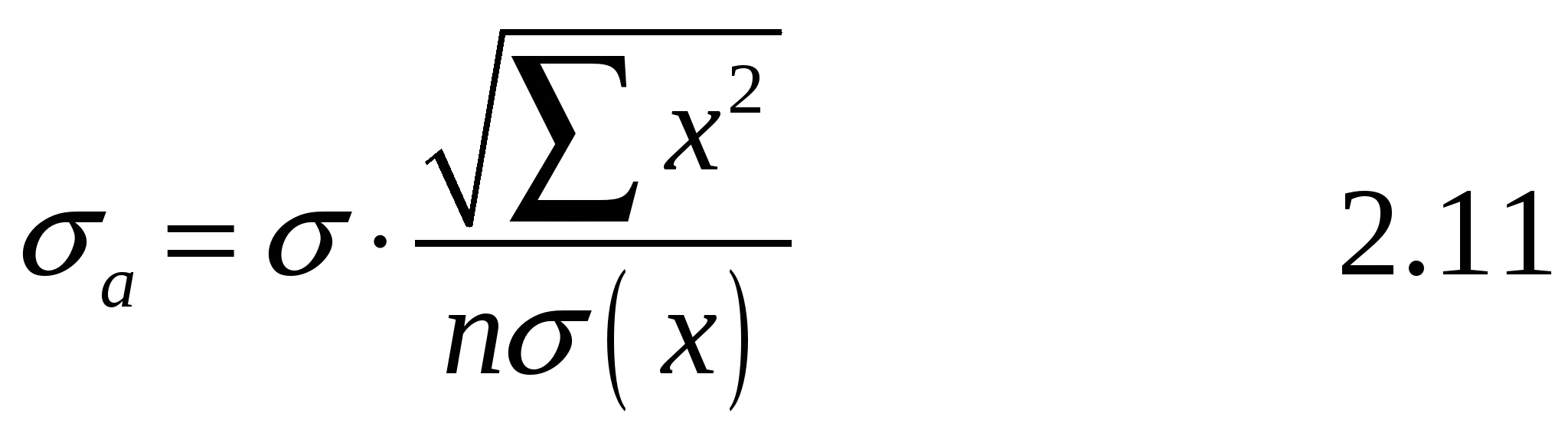Практическая часть
Найдите на сайт http://www.gks.ru/. Выберите данные для построения своей собственной модели. Для этого определите один факторный признак и результативный, т .е. x и у. Например, зависимость стоимость основных фондов (у) от инвестиций (х).
Задание
найти коэффициенты корреляции между X и Y ;
построить регрессионные функции линейной зависимости Y = a + b * X фактора Y от фактора X и исследовать их на надежность по критерию Фишера при уровне значимости 0,05;
найти коэффициент эластичности Y по X при среднем значении X ;
определить надежность коэффициентов регрессии по критерию Стьюдента:
найти доверительные интервалы для коэффициентов регрессии;
построить график регрессионной функции и диаграмму рассеяния.
Исходные данные
Выбираем данные в тыс. руб. по доходам (X) и расходам (Y) на непродовольственные товары 30 домохозяйств (табл. 2.1).
Таблица 2.1
Исходные данные
X
|
30,3
|
37,2
|
46,7
|
51,1
|
52,6
|
53,1
|
53,2
|
55,0
|
56,5
|
57,3
|
Y
|
13,0
|
14,2
|
18,0
|
23,5
|
24,2
|
22,5
|
26,0
|
22,0
|
22,5
|
21,0
|
X
|
58,1
|
58,9
|
63,1
|
65,4
|
66,5
|
67,2
|
68,1
|
70,3
|
74,1
|
75,6
|
Y
|
27,5
|
24,5
|
38,4
|
28,0
|
20,3
|
24,6
|
18,3
|
35,6
|
37,0
|
26,8
|
X
|
77,3
|
79,5
|
80,1
|
84,7
|
85,3
|
87,4
|
96,1
|
99,6
|
107,3
|
114,5
|
Y
|
25,5
|
30,4
|
43,0
|
26,5
|
23,0
|
43,1
|
18,5
|
42,0
|
50,4
|
24,3
|
Решение
1.Найдем коэффициенты корреляции между X и Y
Строим корреляционное поле
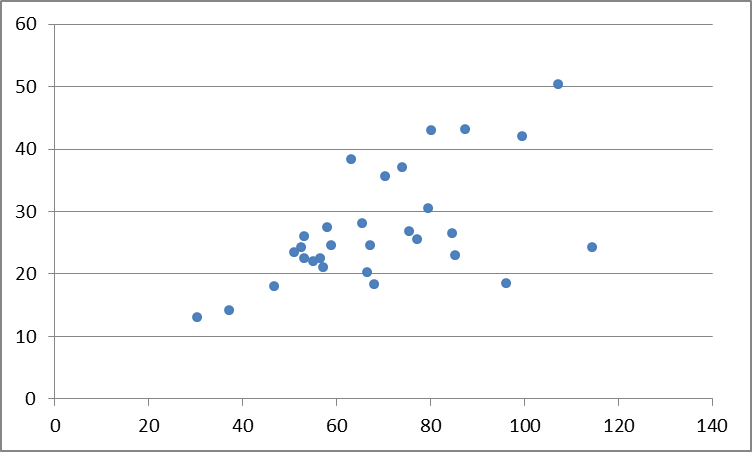
Рис. 2.1.Кореляционное поле
По полученной диаграмме можно предположить, что связь между факторами линейная и прямая.
Составим таблицу промежуточных вычислений (табл. 2.2.)
Таблица 2.2
Талица промежуточных вычислений
№ п/п
|
x
|
y
|
x2
|
y2
|
x·y
|
1
|
30,3
|
13
|
918,09
|
169
|
393,9
|
2
|
37,2
|
14,2
|
1383,84
|
201,64
|
528,24
|
3
|
46,7
|
18
|
2180,89
|
324
|
840,6
|
4
|
51,1
|
23,5
|
2611,21
|
552,25
|
1200,85
|
5
|
52,6
|
24,2
|
2766,76
|
585,64
|
1272,92
|
6
|
53,1
|
22,5
|
2819,61
|
506,25
|
1194,75
|
7
|
53,2
|
26
|
2830,24
|
676
|
1383,2
|
8
|
55
|
22
|
3025
|
484
|
1210
|
9
|
56,5
|
22,5
|
3192,25
|
506,25
|
1271,25
|
10
|
57,3
|
21
|
3283,29
|
441
|
1203,3
|
11
|
58,1
|
27,5
|
3375,61
|
756,25
|
1597,75
|
12
|
58,9
|
24,5
|
3469,21
|
600,25
|
1443,05
|
13
|
63,1
|
38,4
|
3981,61
|
1474,56
|
2423,04
|
14
|
65,4
|
28
|
4277,16
|
784
|
1831,2
|
15
|
66,5
|
20,3
|
4422,25
|
412,09
|
1349,95
|
16
|
67,2
|
24,6
|
4515,84
|
605,16
|
1653,12
|
17
|
68,1
|
18,3
|
4637,61
|
334,89
|
1246,23
|
18
|
70,3
|
35,6
|
4942,09
|
1267,36
|
2502,68
|
19
|
74,1
|
37
|
5490,81
|
1369
|
2741,7
|
20
|
75,6
|
26,8
|
5715,36
|
718,24
|
2026,08
|
21
|
77,3
|
25,5
|
5975,29
|
650,25
|
1971,15
|
22
|
79,5
|
30,4
|
6320,25
|
924,16
|
2416,8
|
23
|
80,1
|
43
|
6416,01
|
1849
|
3444,3
|
24
|
84,7
|
26,5
|
7174,09
|
702,25
|
2244,55
|
25
|
85,3
|
23
|
7276,09
|
529
|
1961,9
|
26
|
87,4
|
43,1
|
7638,76
|
1857,61
|
3766,94
|
27
|
96,1
|
18,5
|
9235,21
|
342,25
|
1777,85
|
28
|
99,6
|
42
|
9920,16
|
1764
|
4183,2
|
29
|
107,3
|
50,4
|
11513,3
|
2540,16
|
5407,92
|
30
|
114,5
|
24,3
|
13110,3
|
590,49
|
2782,35
|
Сумма
|
2072,1
|
814,6
|
154418,13
|
24517
|
59270,77
|
Среднее
|
69,07
|
27,15
|
5147,27
|
817,23
|
1975,69
|
Находим выборочные дисперсии:
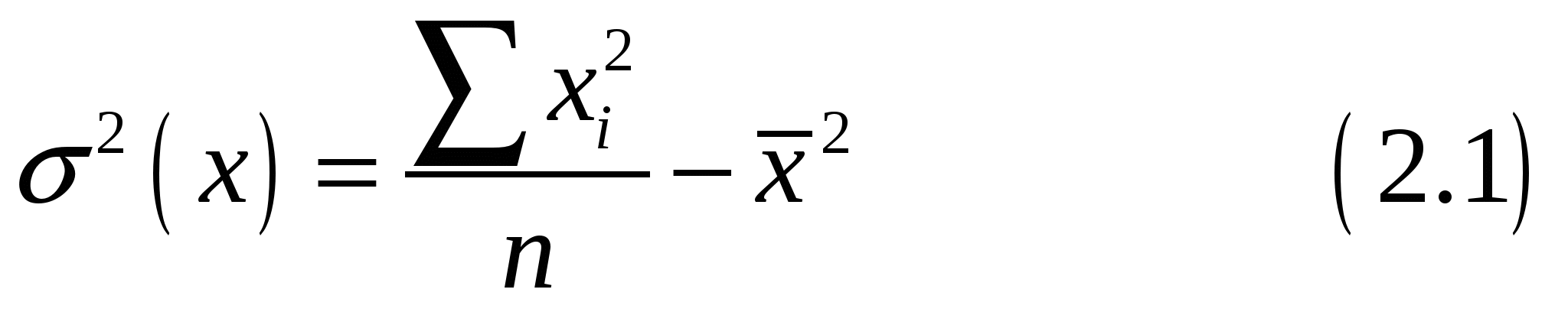
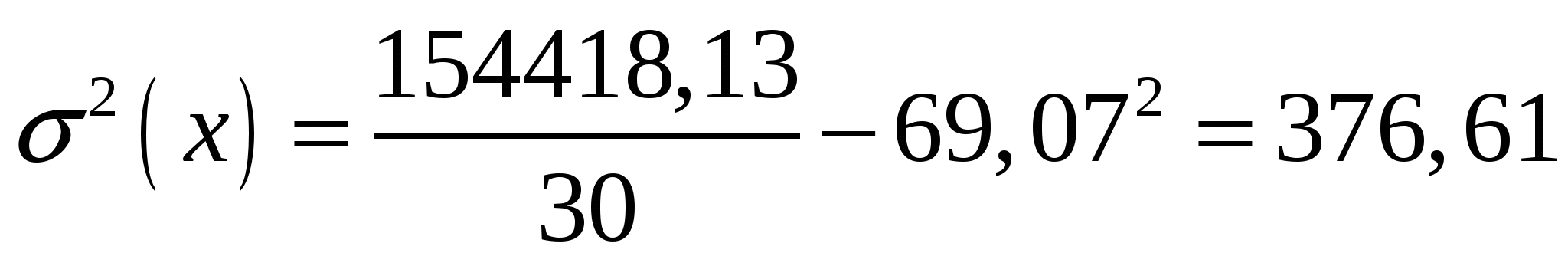
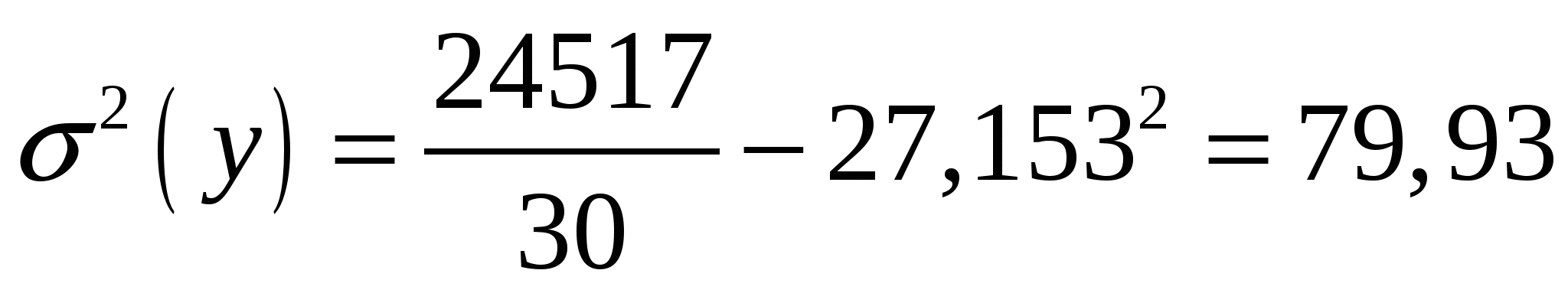
Находим среднеквадратические отклонения:
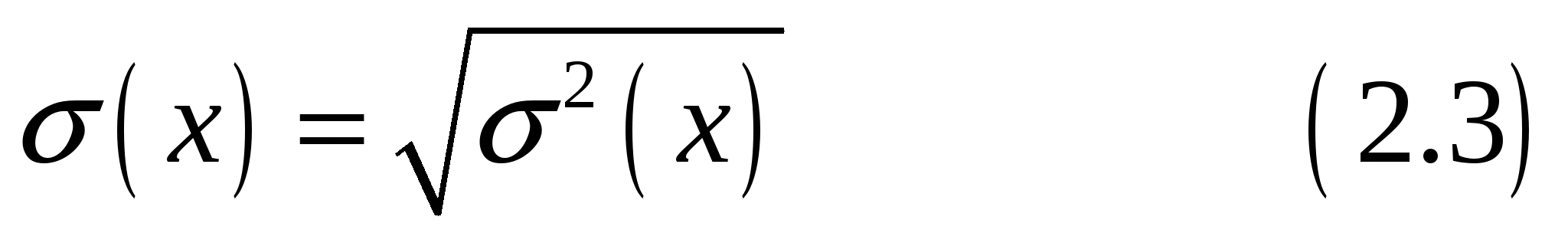
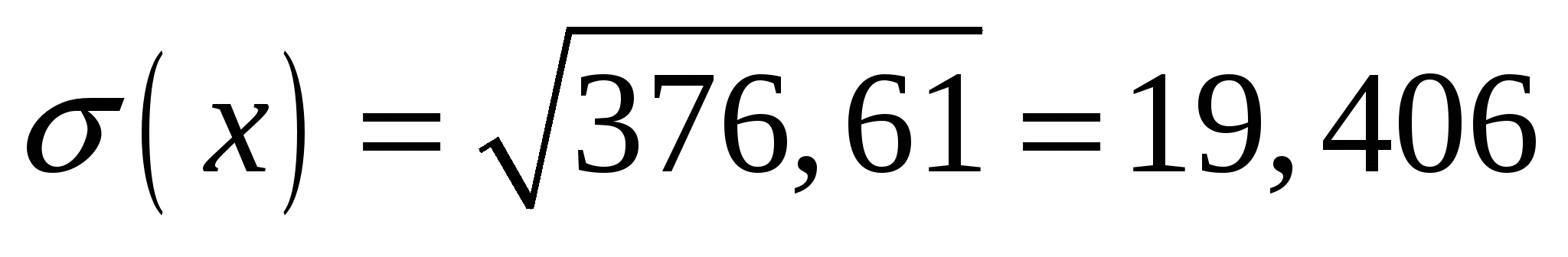
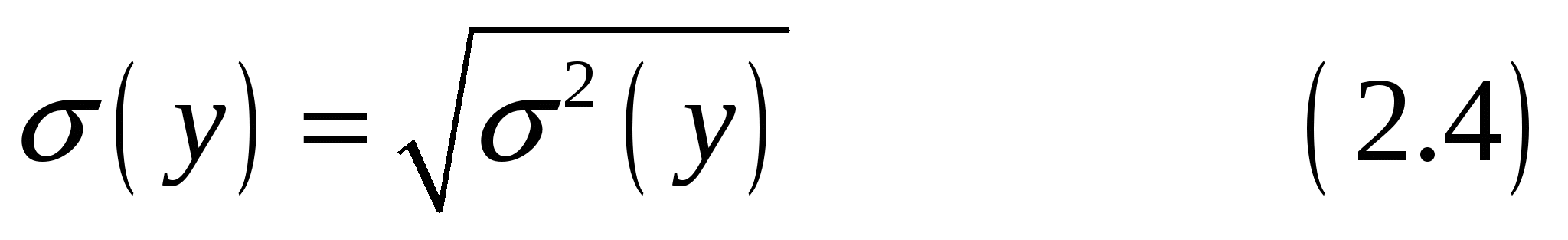
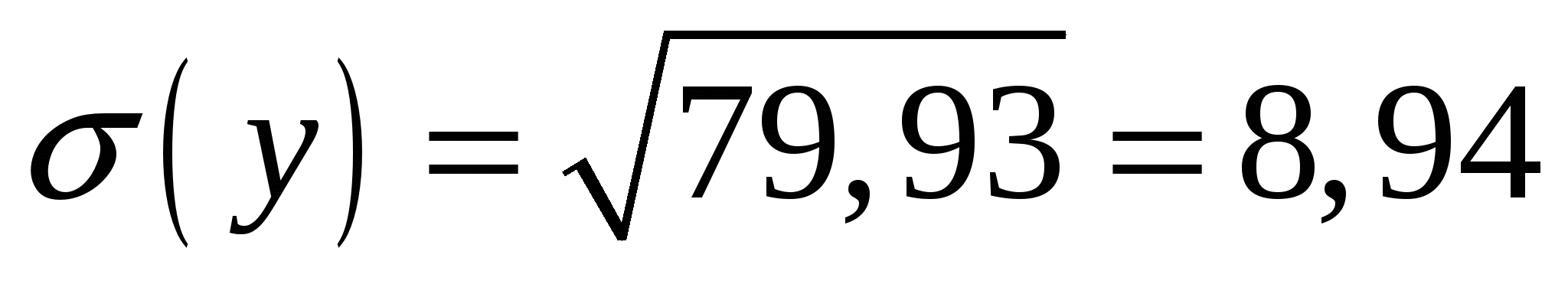
Находим коэффициент корреляции:
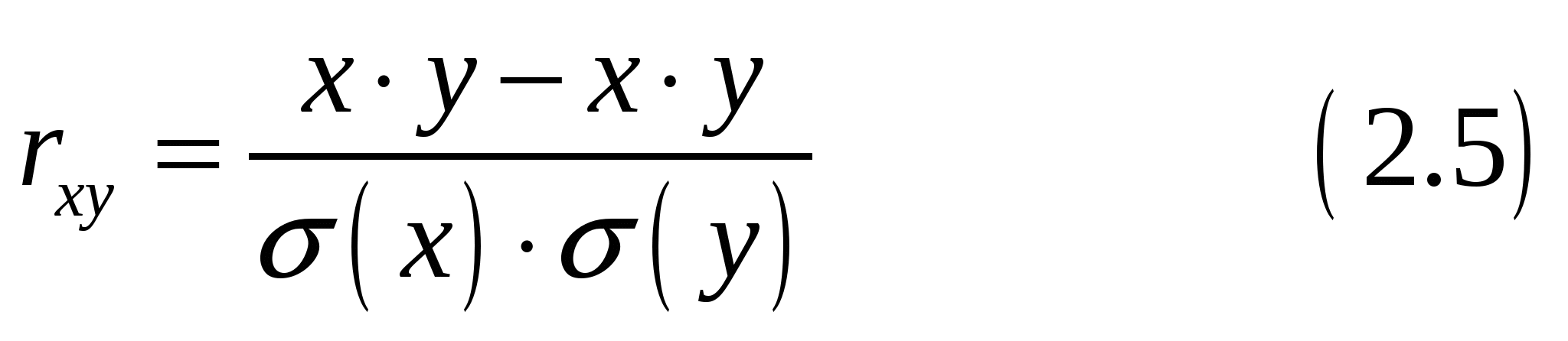
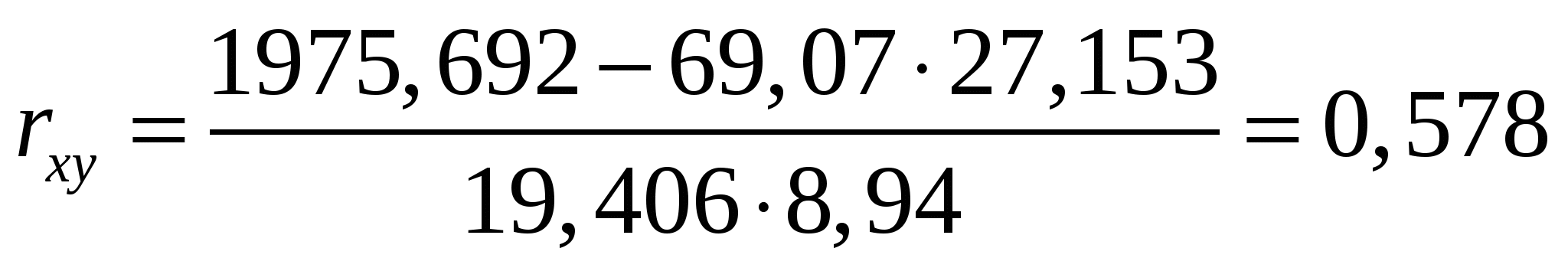
Вывод. Связь между расходами и доходами домохозяйств заметная и прямая.
2.Построим регрессионные функции линейной зависимости 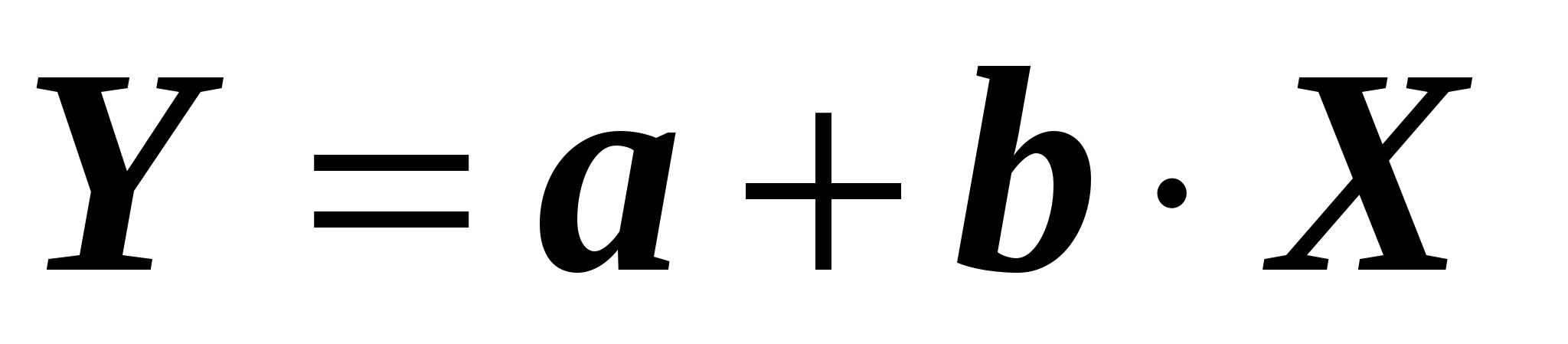 фактора Y от фактора X и исследуем их на надежность по критерию Фишера при уровне значимости 0,05
Определим по МНК оценки парного уравнения регрессии
Найдем коэффициенты уравнения регрессии.
Применим метод наименьших квадратов, для чего решаем систему уравнений:
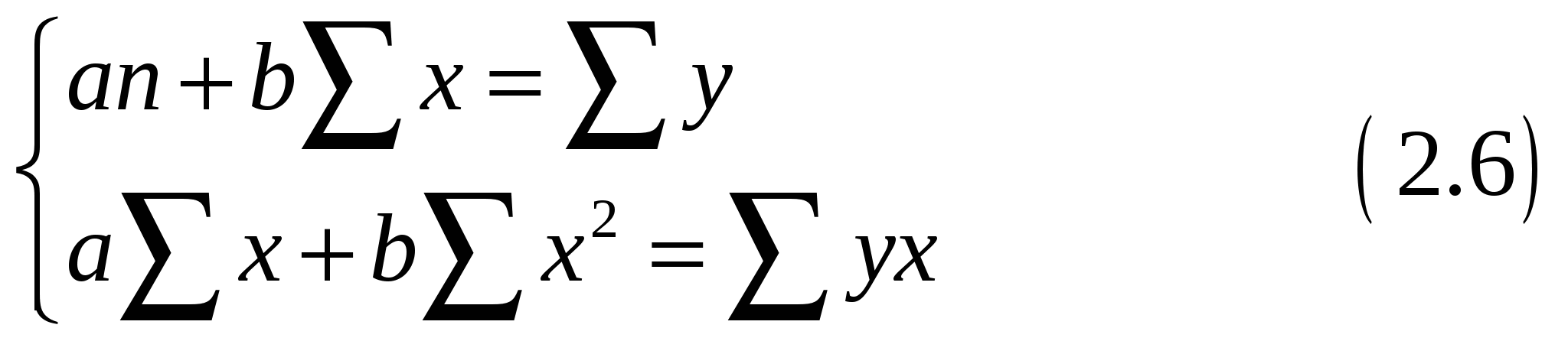
Система уравнений имеет вид:
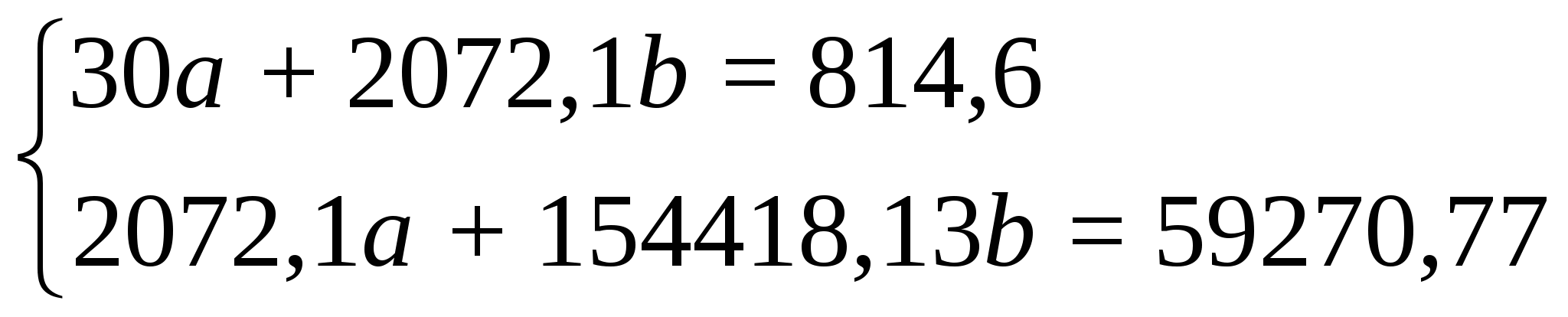
Получаем коэффициенты регрессии: b = 0,2661, a = 8,7744.
Уравнение регрессии имеет вид:
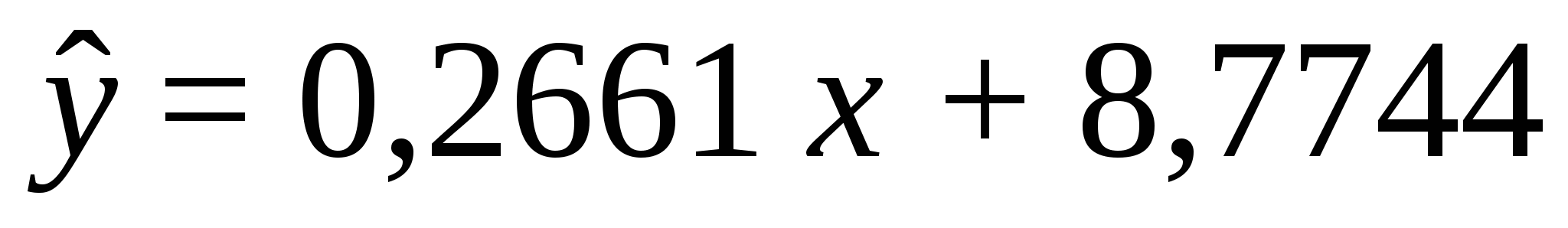
Строим таблицу промежуточных вычислений (табл 2.3).
Таблица 2.3
Талица промежуточных вычислений
№ п/п
|
x
|
y
|
|
|
|
|
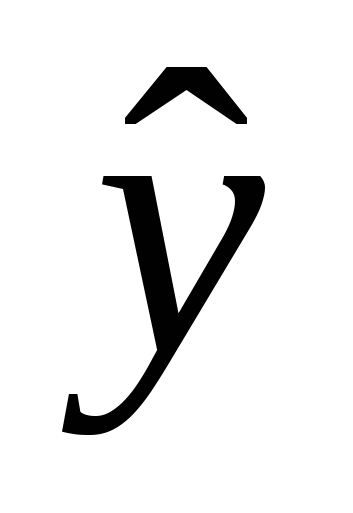
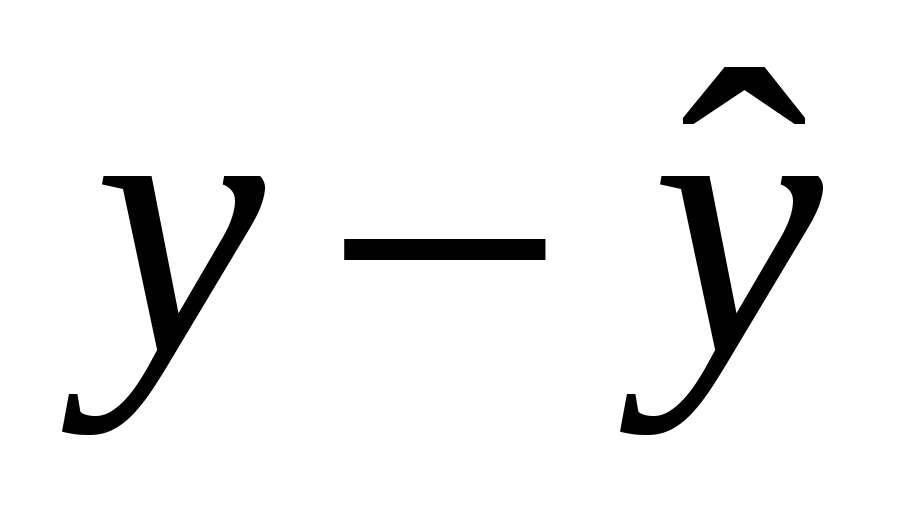
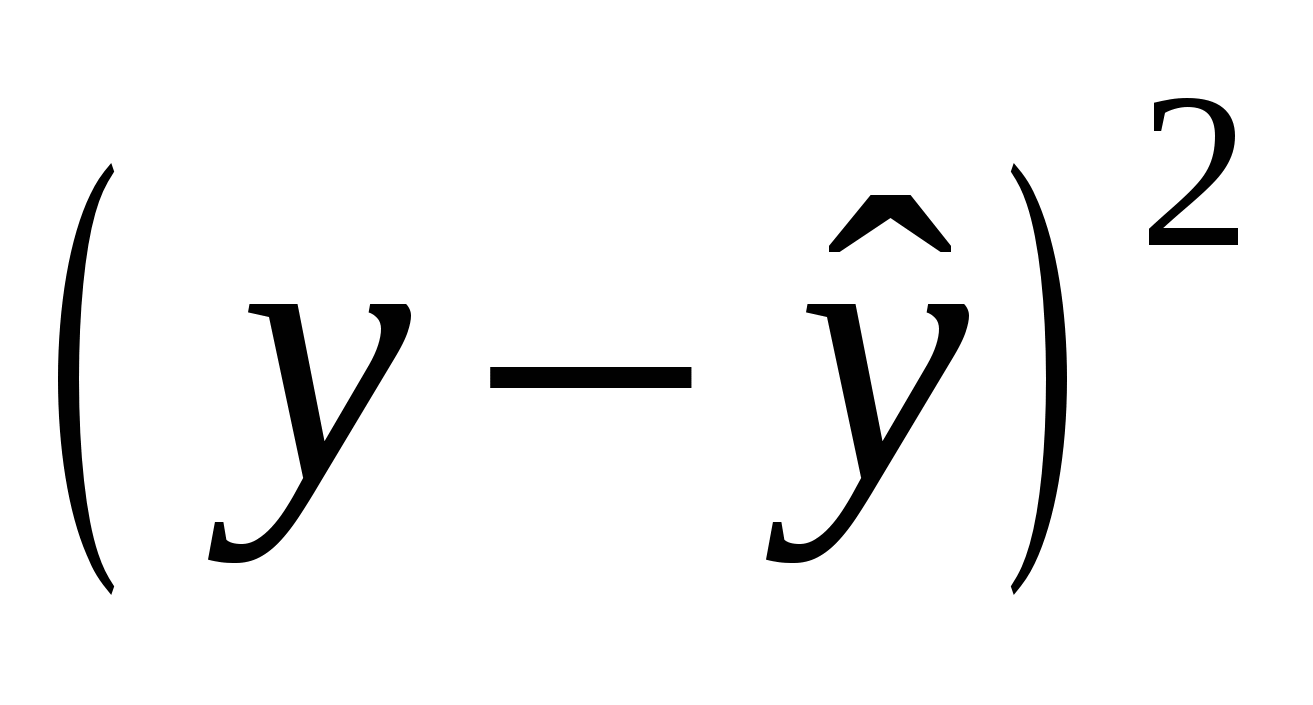
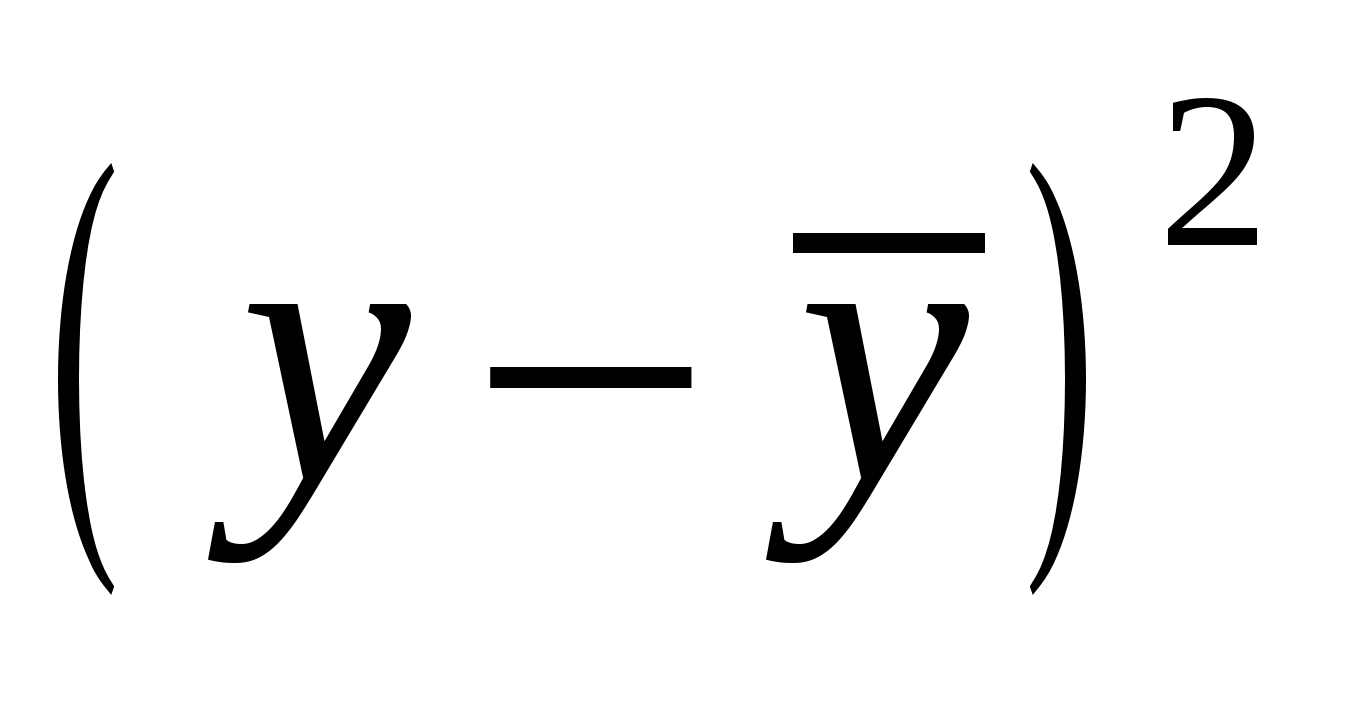
1
|
30,3
|
13
|
16,8338
|
-3,8338
|
14,69802
|
200,2225
|
2
|
37,2
|
14,2
|
18,6692
|
-4,4692
|
19,97375
|
167,7025
|
3
|
46,7
|
18
|
21,1962
|
-3,1962
|
10,21569
|
83,7225
|
4
|
51,1
|
23,5
|
22,3666
|
1,1334
|
1,284596
|
13,3225
|
5
|
52,6
|
24,2
|
22,7656
|
1,4344
|
2,057503
|
8,7025
|
6
|
53,1
|
22,5
|
22,8986
|
-0,3986
|
0,158882
|
21,6225
|
7
|
53,2
|
26
|
22,9252
|
3,0748
|
9,454395
|
1,3225
|
8
|
55
|
22
|
23,404
|
-1,404
|
1,971216
|
26,5225
|
9
|
56,5
|
22,5
|
23,803
|
-1,303
|
1,697809
|
21,6225
|
10
|
57,3
|
21
|
24,0158
|
-3,0158
|
9,09505
|
37,8225
|
11
|
58,1
|
27,5
|
24,2286
|
3,2714
|
10,70206
|
0,1225
|
12
|
58,9
|
24,5
|
24,4414
|
0,0586
|
0,003434
|
7,0225
|
13
|
63,1
|
38,4
|
25,5586
|
12,8414
|
164,9016
|
126,5625
|
14
|
65,4
|
28
|
26,1704
|
1,8296
|
3,347436
|
0,7225
|
15
|
66,5
|
20,3
|
26,463
|
-6,163
|
37,98257
|
46,9225
|
16
|
67,2
|
24,6
|
26,6492
|
-2,0492
|
4,199221
|
6,5025
|
17
|
68,1
|
18,3
|
26,8886
|
-8,5886
|
73,76405
|
78,3225
|
18
|
70,3
|
35,6
|
27,4738
|
8,1262
|
66,03513
|
71,4025
|
19
|
74,1
|
37
|
28,4846
|
8,5154
|
72,51204
|
97,0225
|
20
|
75,6
|
26,8
|
28,8836
|
-2,0836
|
4,341389
|
0,1225
|
21
|
77,3
|
25,5
|
29,3358
|
-3,8358
|
14,71336
|
2,7225
|
22
|
79,5
|
30,4
|
29,921
|
0,479
|
0,229441
|
10,5625
|
23
|
80,1
|
43
|
30,0806
|
12,9194
|
166,9109
|
251,2225
|
24
|
84,7
|
26,5
|
31,3042
|
-4,8042
|
23,08034
|
0,4225
|
25
|
85,3
|
23
|
31,4638
|
-8,4638
|
71,63591
|
17,2225
|
26
|
87,4
|
43,1
|
32,0224
|
11,0776
|
122,7132
|
254,4025
|
27
|
96,1
|
18,5
|
34,3366
|
-15,8366
|
250,7979
|
74,8225
|
28
|
99,6
|
42
|
35,2676
|
6,7324
|
45,32521
|
220,5225
|
29
|
107,3
|
50,4
|
37,3158
|
13,0842
|
171,1963
|
540,5625
|
30
|
114,5
|
24,3
|
39,231
|
-14,931
|
222,9348
|
8,1225
|
Сумма
|
2072,1
|
814,6
|
814,3986
|
-
|
1597,933
|
2397,895
|
Среднее
|
69,07
|
27,15
|
27,14662
|
-
|
53,26444
|
79,92983
|
Оценка значимости построенного уравнения регрессии. Коэффициент детерминации: R2=0,279. Значение коэффициента детерминации свидетельствует о низком качестве уравнения регрессии.
Сделаем выводы о качестве полученной модели с помощью критерия Фишера.
Определим значимость уравнения с помощью критерия Фишера:
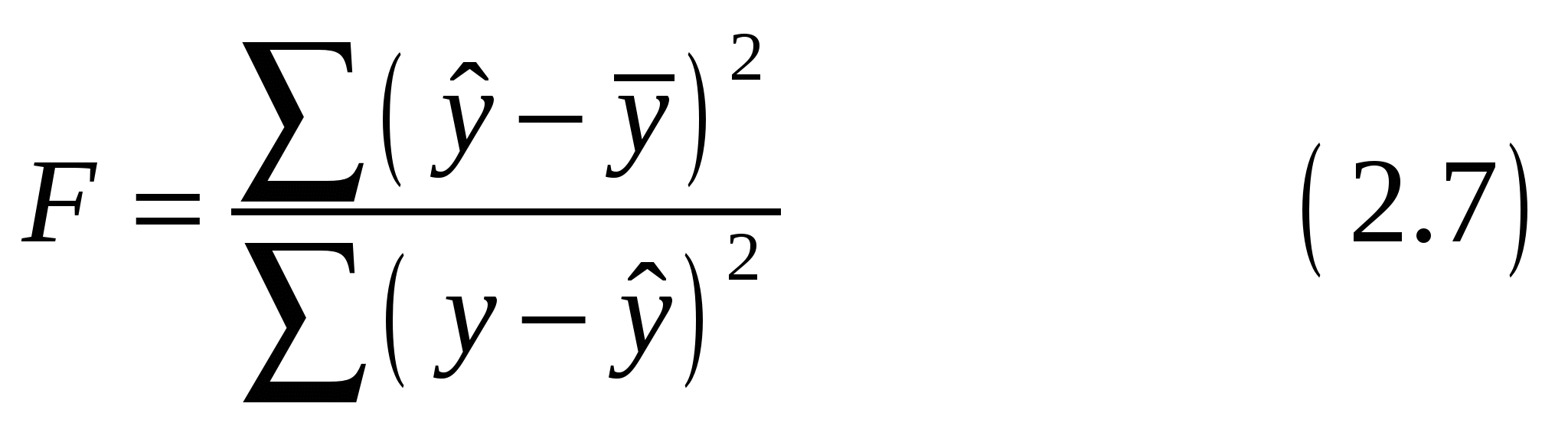
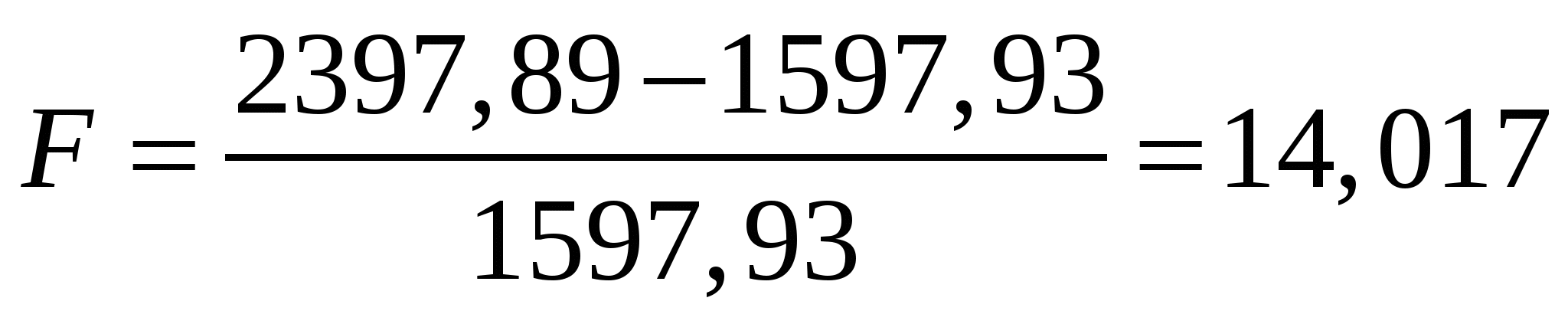
Табличное значение критерия со степенями свободы k1=1 и k2=28, Fтабл = 4,2.
Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
4.Найдем коэффициент эластичности Y по X при среднем значении X:
Коэффициент эластичности меньше 1. Следовательно, при изменении доходов на 1%, расходы изменятся менее чем на 1%. Другими словами - влияние доходов на расходы не существенно.
5.Определим надежность коэффициентов регрессии по критерию Стьюдента
Находим несмещенную оценку дисперсии:
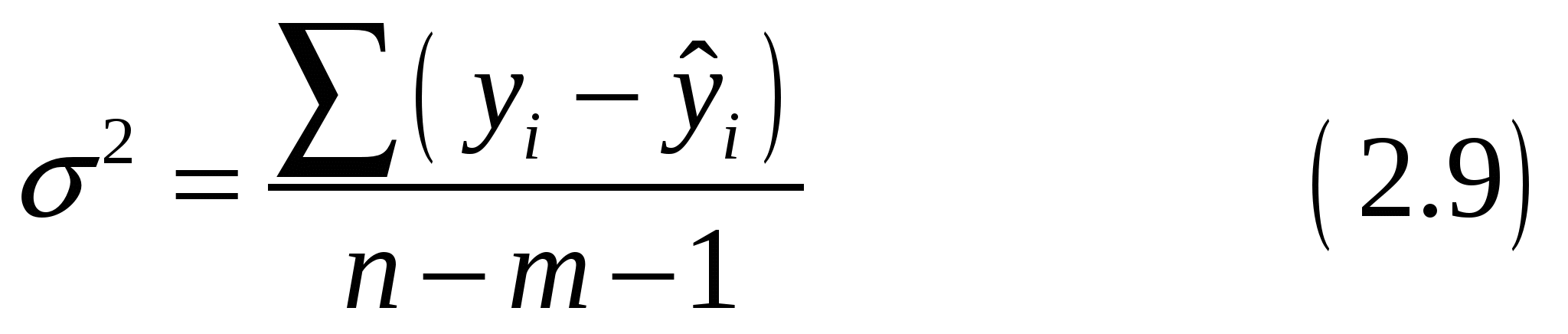
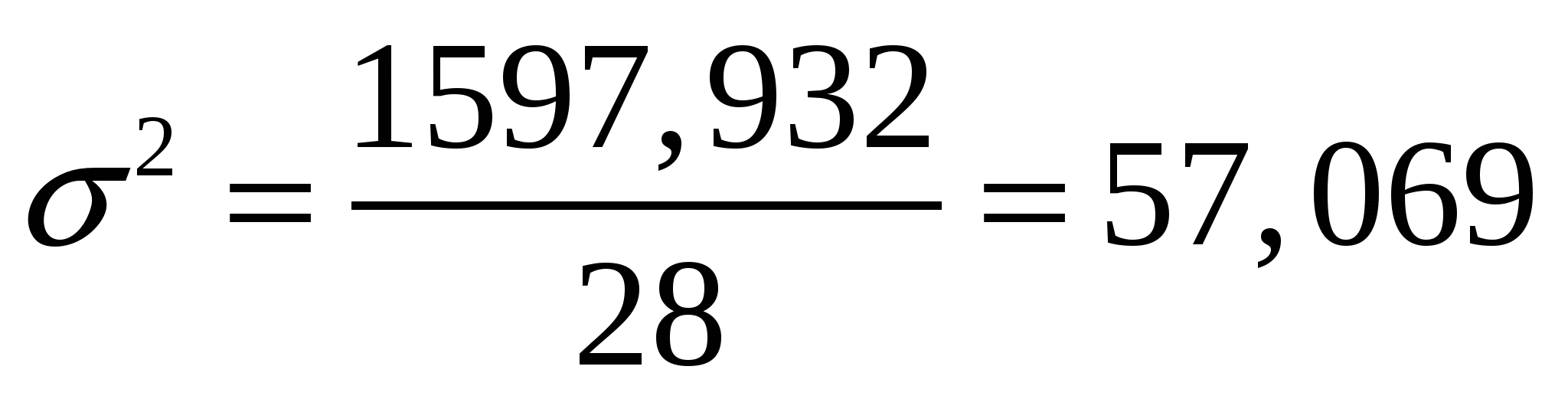
Находим стандартную ошибку оценки:
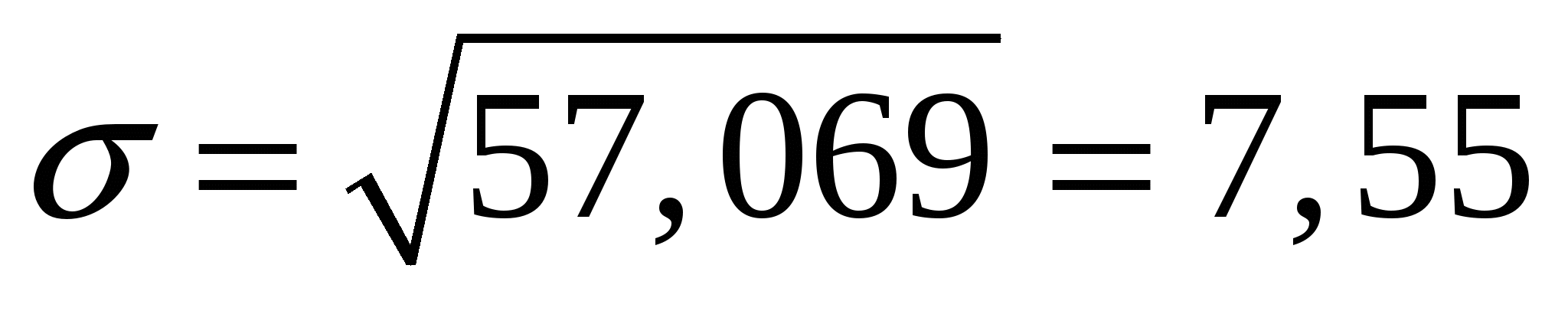
Находим 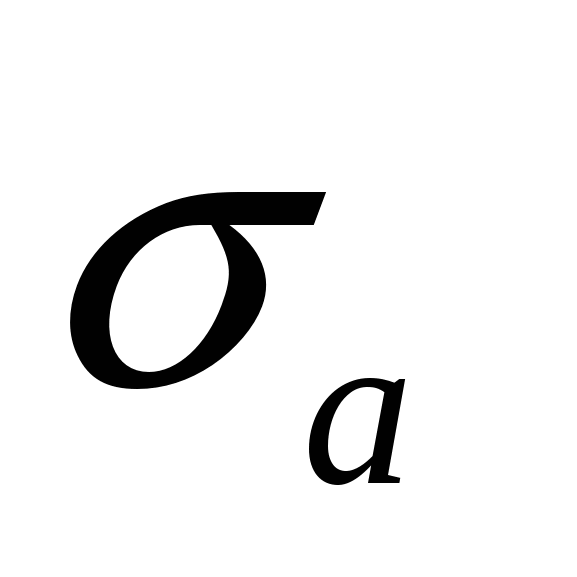 – стандартное отклонение случайной величины  .
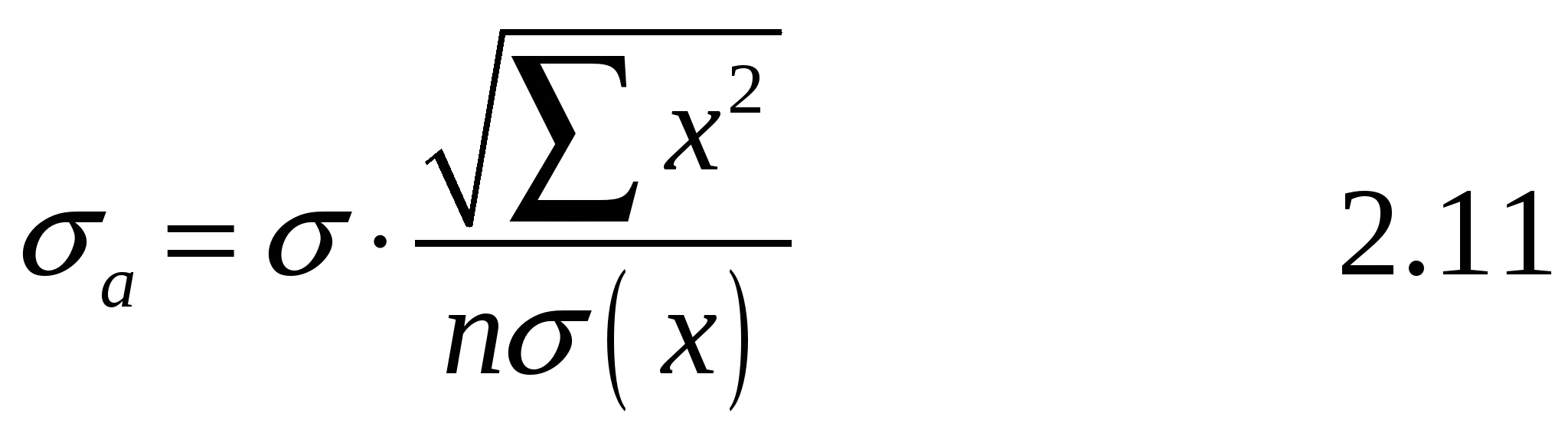
Находим 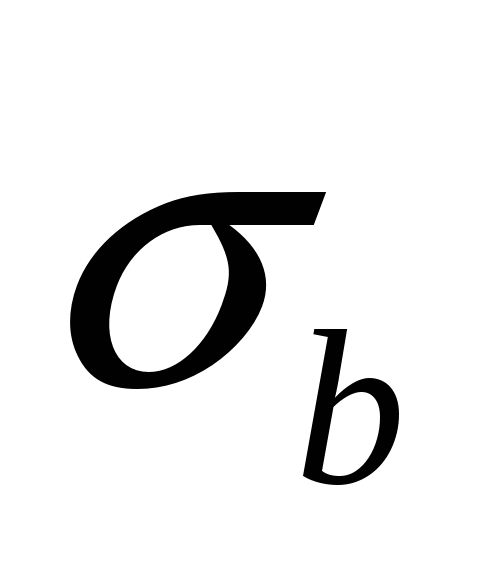 – стандартное отклонение случайной величины  .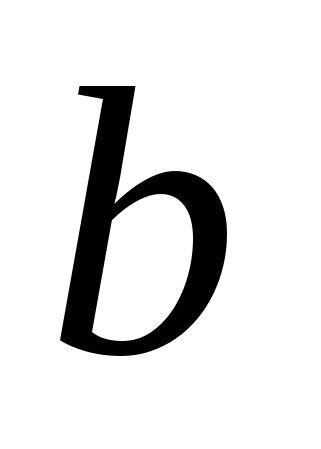
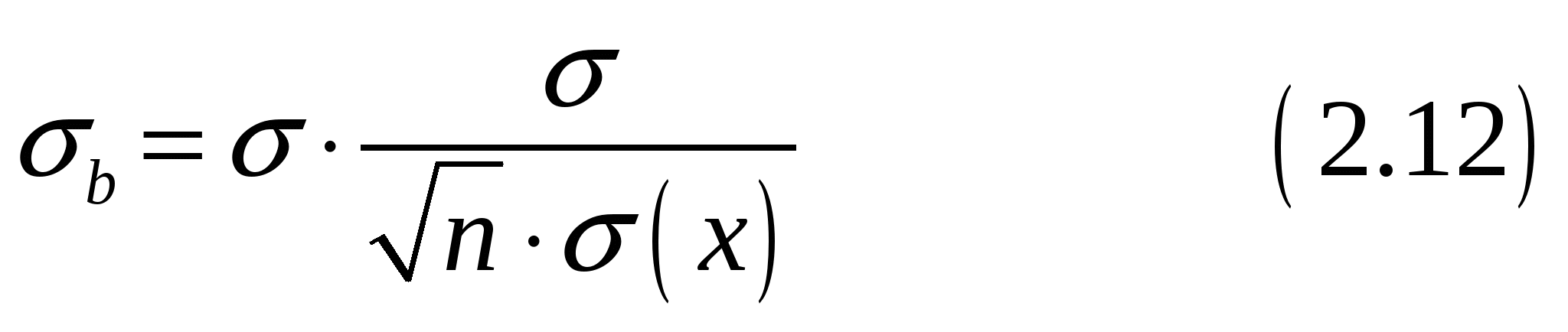
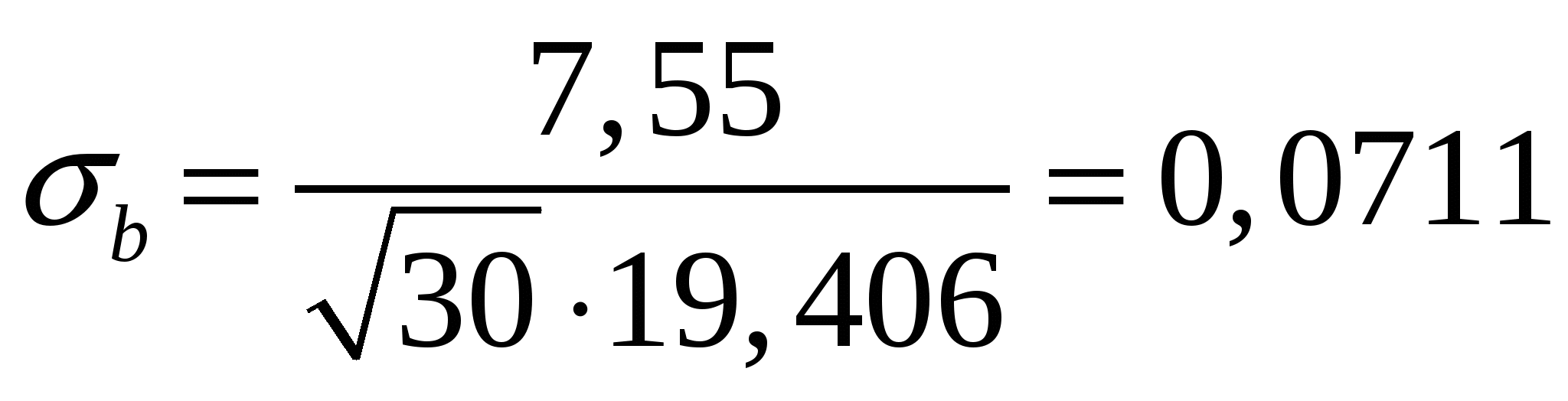
Определяем t-статистику.
Критерий Стьюдента.
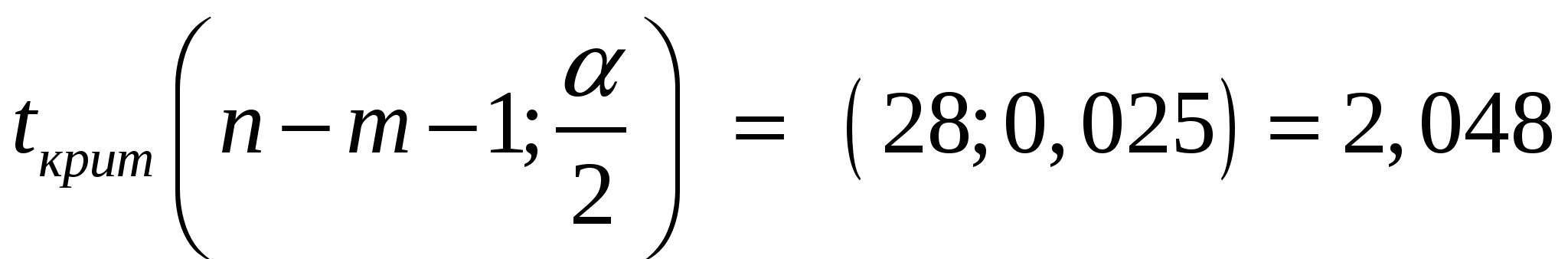
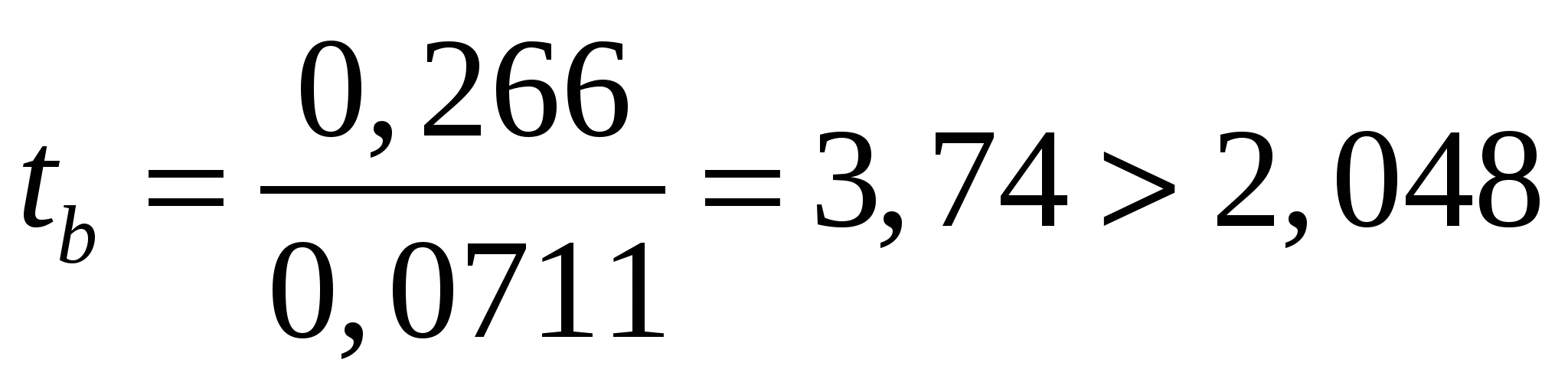
Следовательно, статистическая значимость коэффициента регрессии 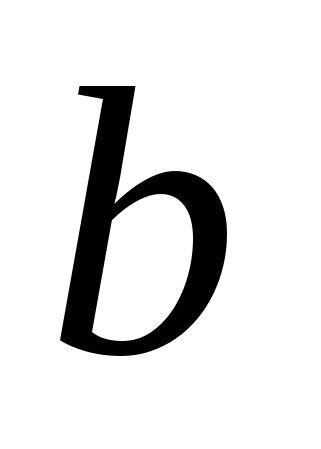подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
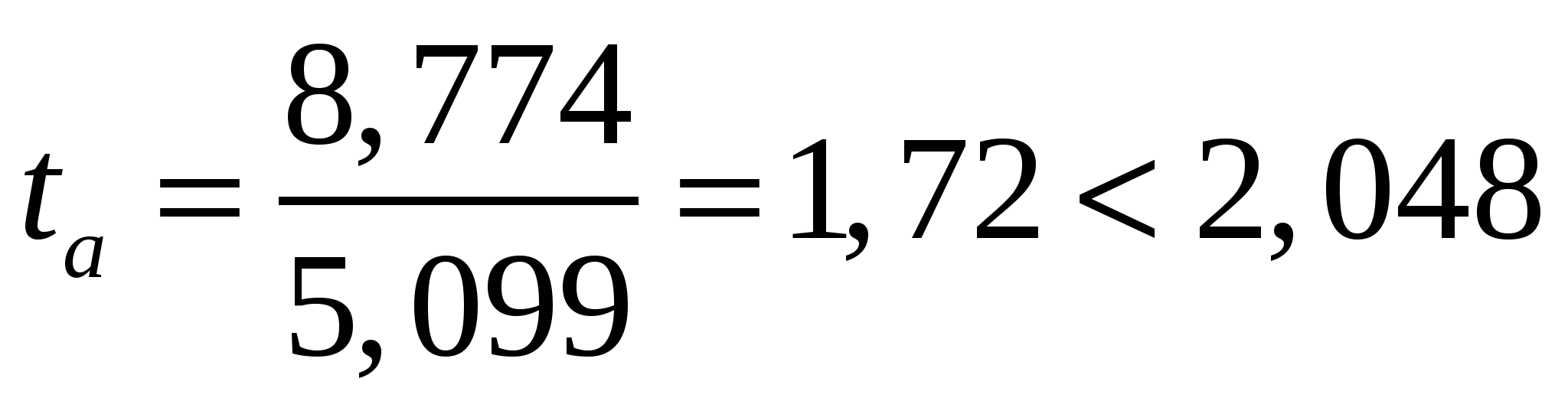
Следовательно, статистическая значимость коэффициента регрессии a не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента). Это означает, что в данном случае коэффициентом a можно пренебречь.
6.Найдем доверительные интервалы для коэффициентов регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
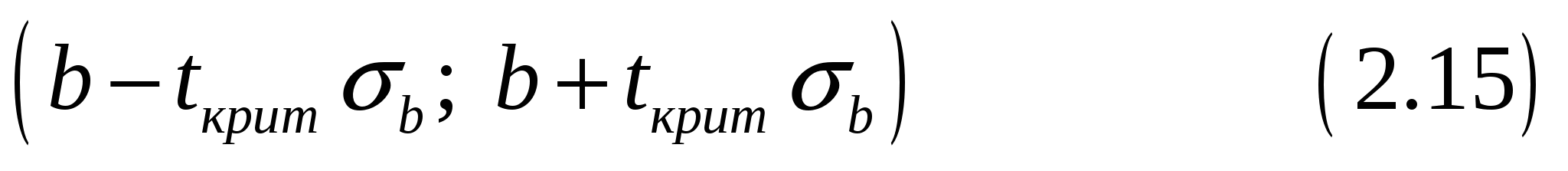
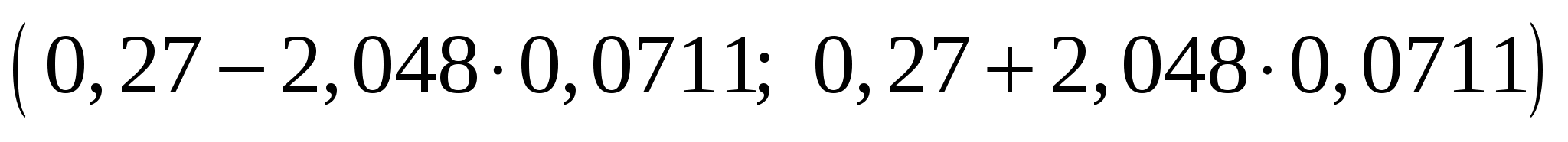
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
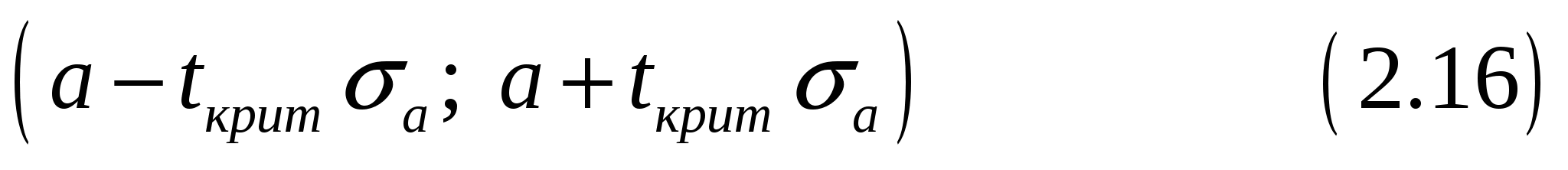
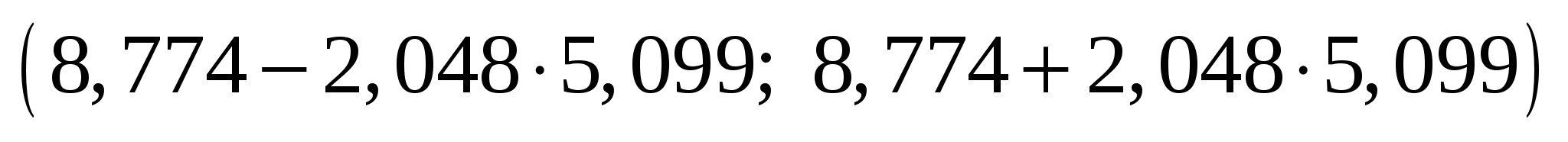
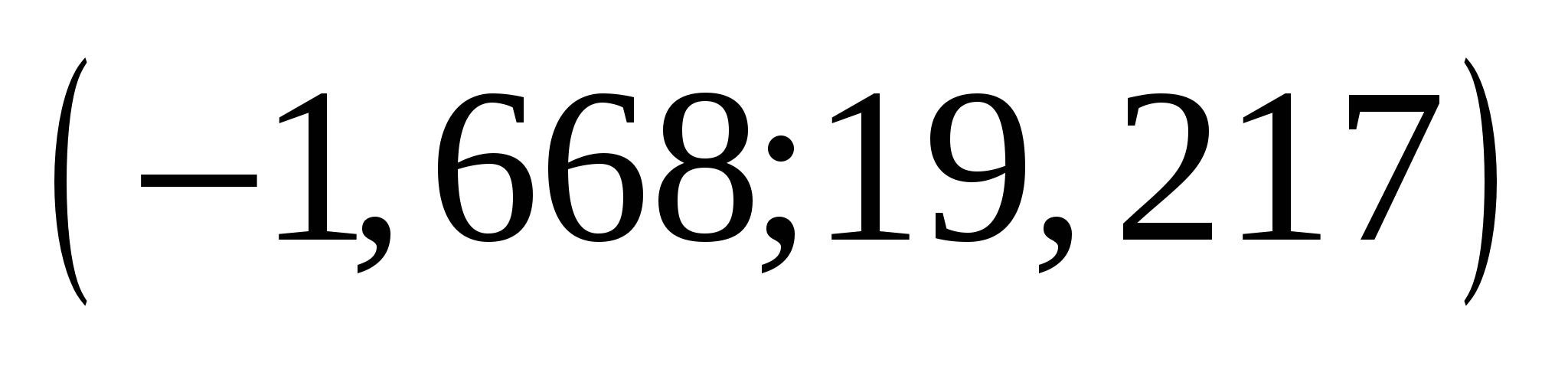
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
Так как точка 0 (ноль) лежит внутри доверительного интервала, то интервальная оценка коэффициента a статистически незначима.
7.Построим график регрессионной функции и диаграмму рассеяния.
Рис. 2.2. График регрессионной функции и диаграмма рассеяния
Литература
Афанасьев В.Н. Анализ временных рядов и прогнозирование: учебник / В.Н. Афанасьев, М.М. Юзбашев. – 2-е изд., перераб. и доп. – М.: Финансы и статистика; ИНФРА-М, 2012 – 320 с.
Бутакова М.М. Экономическое прогнозирование: методы и приемы практических расчетов: учебное пособие / М.М. Бутакова. – 2-е изд. испр. – М.:КНОРУС, 2010. – 168 с.
Практикум по эконометрике / А.В. Гладилин, А.Н. Герасимов, Е.И. Громов. – Ростов н/Д: Феникс, 2011. – 326 с.
Соколов Г.А., Сагитов Р.В. Введение в регрессионный анализ и планирование регрессионных экспериментов в экономике: Учеб. пособие. – М.: ИНФРА-М, 2010. – 202 с.
Эконометрика: учебник / А.В. Гладилин, А.Н. Герасимов, Е.И. Громов. – Ростов н/Д: Феникс, 2011. – 297 с.
|
Скачать 0.53 Mb.