14 задание образец. Задача из пособия "Математика. Огэ 2015. 20 типовых вариантов. Рослова Л. О., Кузнецова Л. В., Шестаков А. С., Ященко И. В."
 Скачать 309.85 Kb.
|
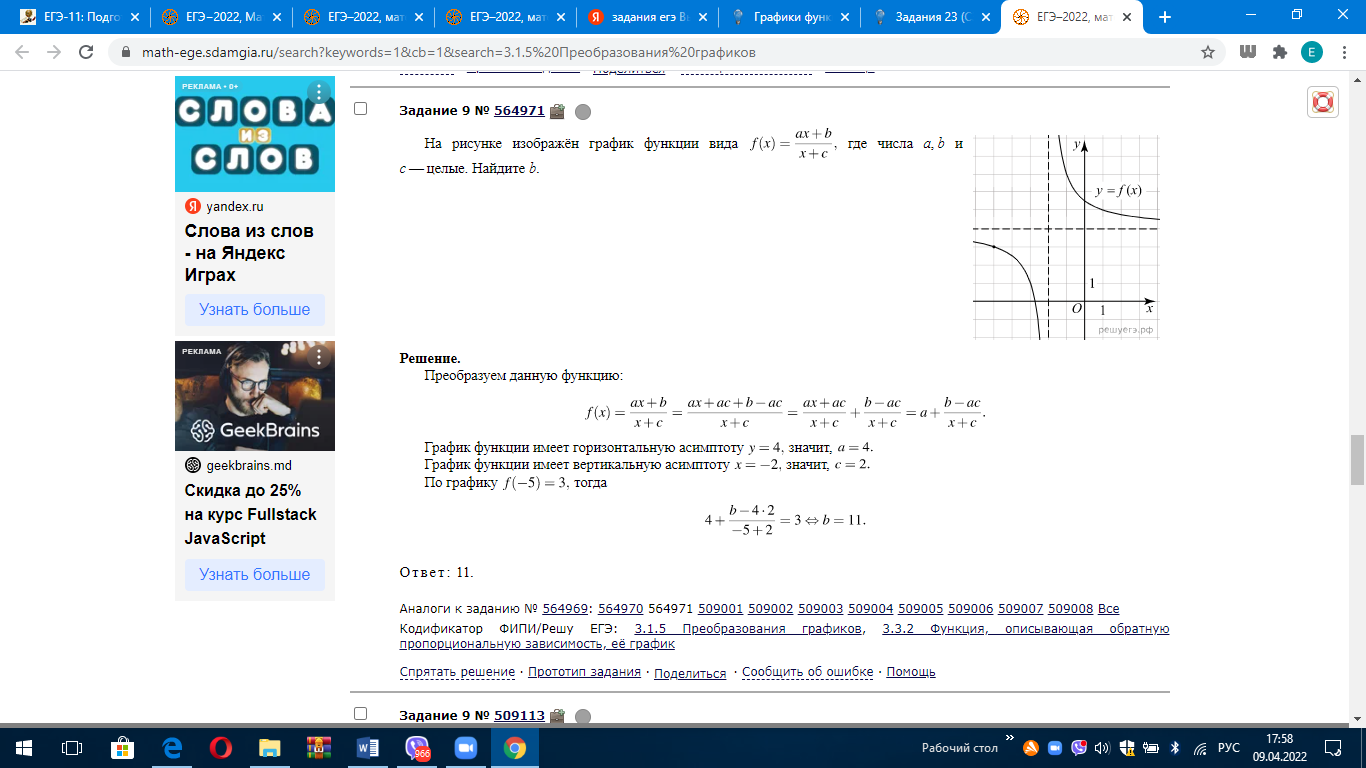 Пример 1. Задача из пособия “Математика. ОГЭ 2015. 20 типовых вариантов. Рослова Л.О., Кузнецова Л.В., Шестаков А.С., Ященко И.В.” Вариант 6, задача 23. Постройте график функции 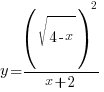 . Найдите все значения а, при которых прямая  не имеет с графиком данной функции общих точек.Сначала займемся областью определения данной функции:  , так как на ноль делить нельзя, и  , то есть   ,так как подкоренное выражение неотрицательно.Теперь можно преобразовать выражение, попробовать его упростить. Получим: 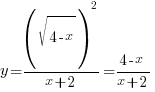 Выделим целую часть: 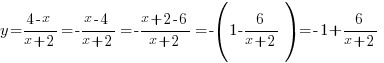 Теперь картина стала совсем ясной: имеем обычную гиперболу с коэффициентом 6. 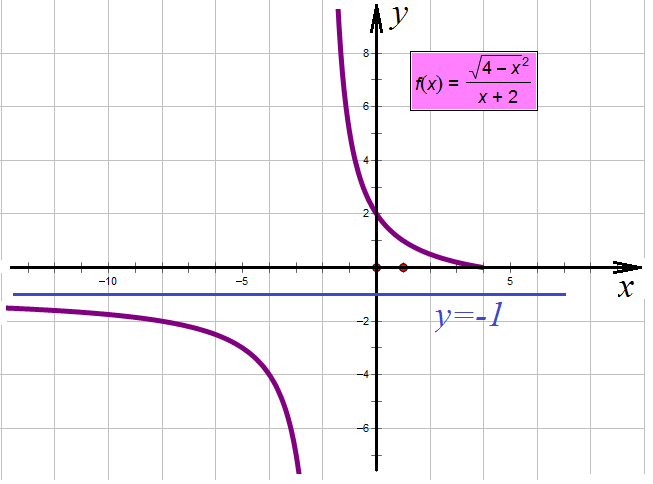 , которую сместили влево на 2 единицы  , а потом сместили на одну единицу вниз:  . Причем существует эта наша гипербола, согласно области определения, только до точки 4, а в точке (-2) имеет вертикальную асимптоту. Строим: К задаче 1 Видно, что прямая  не будет иметь с графиком общих точек, так как является горизонтальной асимптотой. Также все прямые, лежащие выше нее, до прямой  , также не будут иметь общих точек с данной функцией, а сама прямая – будет уже иметь точку пересечения с гиперболой, так как неравенство области определения – нестрогое.Ответ:  )Пример 2. Задача из пособия “Математика. ОГЭ 2015. 20 типовых вариантов. Рослова Л.О., Кузнецова Л.В., Шестаков А.С., Ященко И.В.” Вариант 7, задача 23. Постройте график функции 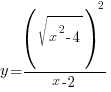 . Найдите все значения а, при которых прямая не имеет с графиком данной функции общих точек.Область определения данной функции:  , так как на ноль делить нельзя, и  , то есть  ( ,так как подкоренное выражение неотрицательно.Теперь можно преобразовать выражение, попробовать его упростить. Получим: 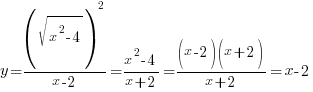 Имеем прямую, параллельную биссектрисе 1 и 3 квадрантов, смещенную вниз по оси ординат на 2 единицы, и не существующую на отрезке (-2; 2]. Строим: 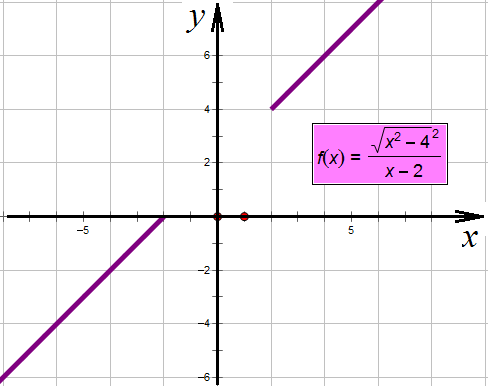 К задаче 2 По графику видно, что любая прямая, параллельная оси х и проходящая через точки оси y с координатами (0;4] не будет иметь общих точек с графиком функции. Ответ:  ( .Пример 3. Задача из пособия “Математика. ОГЭ 2015. 20 типовых вариантов. Рослова Л.О., Кузнецова Л.В., Шестаков А.С., Ященко И.В.” Вариант 18, задача 23. Постройте график функции  . Найдите все значения p, при которых прямая  имеет с графиком данной функции 2 общие точки.Кстати, здесь можно найти статью о том, как строить графики функций с модулями. Область определения  Раскрываем модуль. В положительной полуплоскости (правой)  , в отрицательной полуплоскости (левой)  . Тогда в правой полуплоскости имеем  , в левой полуплоскости .Функция представляет собой прямую  , которую можно двигать вверх-вниз на p единиц. Построим график заданной функции и подвигаем по нему прямую : К задаче 3 Видим, что между двумя крайними положениями прямой , показанными синим цветом, то есть при  и  , когда имеем только одну общую точку, располагаются прямые, имеющие с графиком функции две общие точки. Тогда две общие точки будем иметь при  .Ответ: .Пример 4. Задача из пособия “Математика. ОГЭ 2015. 20 типовых вариантов. Рослова Л.О., Кузнецова Л.В., Шестаков А.С., Ященко И.В.” Контрольный вариант, задача 23. Постройте график функции 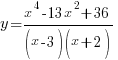 . Найдите все значения а, при которых прямая  имеет с графиком данной функции ровно одну общую точку.Область определения данной функции – вся числовая ось, кроме точек (-2) и (3), так как в этих точках знаменатель обращается в ноль. Теперь упростим выражение, задающее график функции: 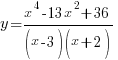Разложим числитель на множители: 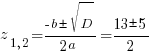 , где  . ,  . . .Имеем: 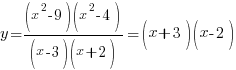 Получили параболу. Точки пересечения с осью x – (-3) и (2) – это корни уравнения  . Вершина параболы:  в точке (-0.5; -6.25). Не забудем о двух выколотых точках! Строим: К задаче 4 Таким образом, если прямая пройдет через эти выколотые точки, то она неминуемо пересечет только одну ветвь параболы. Тогда необходимо определить ординаты выколотых точек, для этого подставим их абсциссы в уравнение, задающее функцию. Получим две точки: (-2; -4) и (3; 6).Однако надо учесть еще и то, что парабола всегда “растет” быстрее прямой, поэтому, если прямая пройдет через вершину параболы и через начало координат, то она уже не будет пересекаться с параболой вверху, просто “не догонит”. Поэтому еще один вариант ответа –  .Ответ: с=-4 и с=6, Пример 5. Постройте график функции 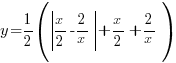 и определите по графику, сколько общих точек будет иметь график этой функции с прямой при различных значениях параметра с.Трудно себе представить вот так, сразу, без подготовки, что называется, “на вскидку”, как будет выглядеть график этой функции. Но мы видим модуль – это часто делает функцию кусочной. То есть на одном интервале она задается одним выражением, а на другом интервале – другим. Поэтому прежде всего нужно определить, в каких точках подмодульное выражение меняет знак. Для этого приведем оба слагаемых подмодульного выражения к одному знаменателю:  . Теперь приравняем к нулю числитель и знаменатель полученного выражения: ,   ,  Нарисуем строго друг под другом числовые прямые и покажем на них динамику смены знака числителем и знаменателем, тогда можно будет определить, где и как меняет знак все подмодульное выражение. 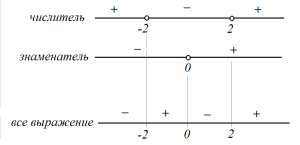 Раскрываем модуль На луче (  раскроем модуль с отрицательным знаком, на интервале (-2;0) – с положительным, на полуинтервале (0;2] вновь с отрицательным, и, наконец, на луче  – также с положительным. Тогда:На первом и третьем: 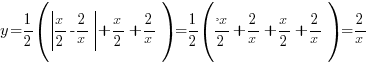 На втором и четвертом: 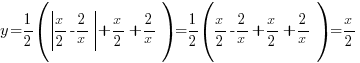 Строим функцию по интервалам: 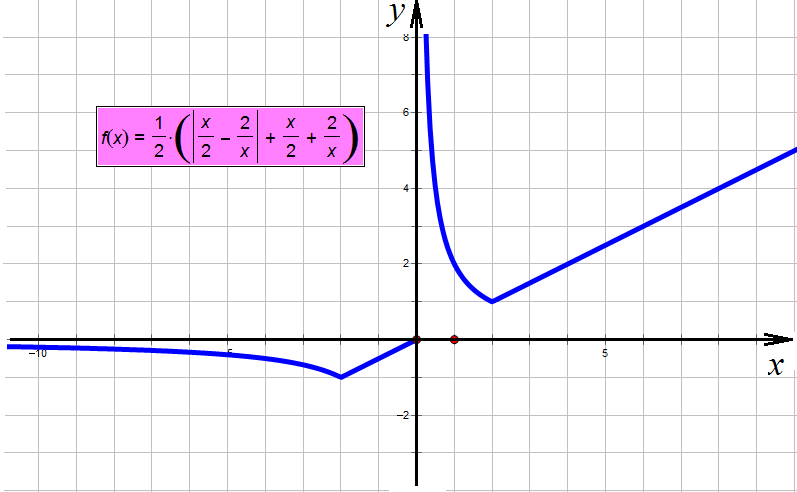 К задаче 5 Тогда становится видно, что при с=-1 и с=1 имеем одну точку пересечения, при  и  – два, а при  ) – ни одного. |