эмм. ЭММ. Задача к теме 3 3 Задача 1 к теме 4 9 Задача 2 к теме 4 11 Задача к теме 5 15

• Название: Задача к теме 3 3 Задача 1 к теме 4 9 Задача 2 к теме 4 11 Задача к теме 5 15
• Дата: 16.02.2022
• Размер: 477.43 Kb.
• Имя файла: ЭММ.docx
• Тип: Задача; #364630
• страница: 4 из 4

Задача к теме 5

По имеющимся данным, представленным в таблице, получена матрица парных коэффициентов корреляции.

Таблица 8 – Исходные данные задачи к теме 5

Номер района, а/б	Кол-во комнат	Общая площадь	Жилая площадь	Площадь кухни	Этаж, средние/крайние	Дом, кирп/ пан	Срок сдачи, ч/з _ мес.	Стоимость квартиры, тыс. $
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Y
1	1	39,8	19	7	1	2	7	20,5
1	1	53,2	19,4	9	2	1	3	23,6
2	1	46	18	9	2	2	1	14,2
…	…	…	…	…	…	…	…	…
1	5	370	180	35	2	2	2	190
2	5	231,2	149	30	2	2	2	139,2
2	6	251,5	167	32,5	2	1	5	157,2

Таблица 9 – Матрица парных коэффициентов корреляции, полученная на основании исходных данных

	X1	X2	X3	X4	X5	X6	X7	X8	Y
X1	1	0	0	0	0	0	0	0	0
X2	-0,0143	1	0	0	0	0	0	0	0
X3	-0,0375	0,9766	1	0	0	0	0	0	0
X4	-0,2663	0,7628	0,8391	1	0	0	0	0	0
X5	0,0341	0,1064	0,8621	0,7973	1	0	0	0	0
X6	-0,2719	0,0663	0,5121	-0,0341	-0,0084	1	0	0	0
X7	-0,5308	0,0068	0,0711	-0,1763	0,0328	0,0680	1	0	0
X8	0,4406	0,0044	0,4438	0,0101	0,2764	-0,1068	-0,0354	1	0
Y	-0,4033	0,8333	0,9101	0,2703	0,7703	0,603	0,8001	0,7473	1

Задание:

1. 
   Укажите, какие фиктивные переменные использованы в модели.
   
2. 
   Проверьте факторы на мультиколлинеарность и устраните её.
   
3. 
   Запишите новое уравнение многофакторной регрессии, после устранения мультиколлинеарности.
   

Решение:

С помощью матрицы коэффициентов корреляции оценивается теснота связи зависимой переменной и факторов. Между переменными Y и X₁ наблюдается обратная связь (отрицательный коэффициент корреляции). Прямой и достаточно тесной является связь между Y и X₂, X₃ и X₇ (коэффициенты корреляции имеют значения близкие к 1).

В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств: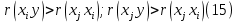



Если одно из неравенств не соблюдается, то исключается тот параметр X_j или X_i, связь которого с результативным показателем Y оказывается наименее тесной.

Для отбора наиболее значимых факторов X_i учитываются следующие условия:

• 
  связь между результативным признаком и факторным должна быть выше межфакторной связи;
  
• 
  связь между факторами должна быть не более 0,7. Если в матрице есть межфакторный коэффициент корреляции rx_jx_i > 0,7, то в данной модели множественной регрессии существует мультиколлинеарность;
  
• 
  при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними.
  

Оценим связь между факторами (X₁,…X₈). Между парами переменных (X₂, X₃), (X₂, X₄), (X₃, X₄), (X₃, X₅), (X₄, X₅) существует сильная связь (r>0,7), т.е. наблюдается явление мультиколлинеарности.

Анализ последней строки матрицы коэффициентов корреляции позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых |ryx_i| < 0,5 исключают из модели. Таких факторов два – X₁ и X₄. Исключим их из модели. Тогда зависимой переменной останется Y (стоимость квартиры, тыс. $), объясняющими выступают 6 переменных: X₂ - кол-во комнат, X₃ - общая площадь, X₅ - площадь кухни, X₆ - этаж, средние/крайние, X₇ – материал дома, X₈ – срок сдачи. Линейная модель будет иметь вид: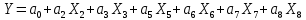