эмм. ЭММ. Задача к теме 3 3 Задача 1 к теме 4 9 Задача 2 к теме 4 11 Задача к теме 5 15
 Скачать 477.43 Kb. Скачать 477.43 Kb.
|
СодержаниеЗадача к теме 3 3 Задача 1 к теме 4 9 Задача 2 к теме 4 11 Задача к теме 5 15 Задача к теме 3Имеются некоторые данные об объеме продаж за 24 месяца: Таблица 1 – Исходные данные к задаче по теме 3
На основе данных за 1-ый год (1-12 месяцы) спрогнозировать объем продаж на 2-ой год (13-24 месяцы) по уравнению линейного тренда, а также с помощью среднего абсолютного прироста и среднего темпа роста. По каждой ситуации рассчитать ошибку прогноза, сопоставив расчетные данные с фактическими, в т.ч. по сумме за год. Решение: Для выявления наличия тенденции в ряду, построим график по исходным данным за первый год и проведем визуальный анализ. 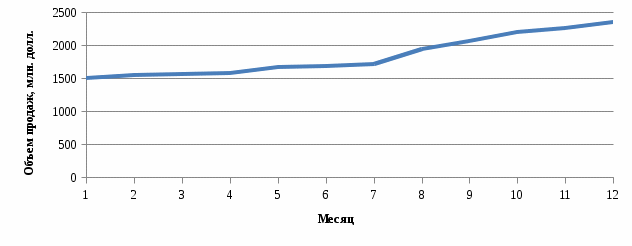 Рисунок 1 – График объема продаж в первый год Визуальный анализ графика позволяет сделать предварительный вывод о том, что временной ряд содержит тенденцию среднего уровня ряда - возрастающий тренд и он, предположительно - линейный, так как оборот, в среднем, увеличивается во времени. Линейное уравнение тренда имеет вид: 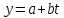 Находим параметры уравнения методом наименьших квадратов. Составим систему уравнений: 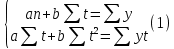 Составим расчетную таблицу. Таблица 2 – Расчетная таблица для нахождения параметров уравнения тренда
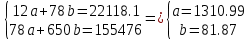 Уравнение тренда: 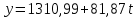 Рассчитаем прогнозные значения (таблица 3) и оценим качество уравнения тренда с помощью средней относительной ошибки аппроксимации. 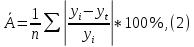 где yt – расчетное значение по уравнению. Таблица 3 – Расчет прогнозных значений и средней относительной ошибки
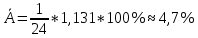 Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным. Следовательно, данное уравнение можно использовать в качестве тренда. Для определения размеров погрешности рассчитаем коэффициент несоответствия Тейла по формуле: 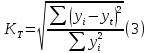 Этот показатель изменяется от 0 до 1. Чем ближе его значение к нулю, тем лучше результаты прогнозирования. 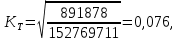 что позволяет сделать вывод о достаточно высоком качестве построенной модели. что позволяет сделать вывод о достаточно высоком качестве построенной модели.Для наглядности построим графики фактических и прогнозных значений (рисунок 2). 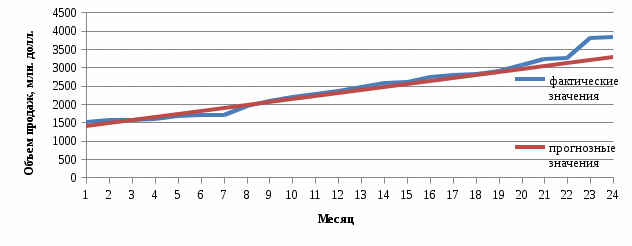 Рисунок 2 – График объема продаж за 24 месяца (фактический и прогнозный) Осуществим расчет прогнозных значений с помощью среднего абсолютного прироста и среднего темпа роста (таблица 4). Для расчетов будем использовать следующие формулы: Абсолютный прирост: цепной: 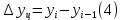 базисный: 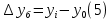 Темп роста: цепной: 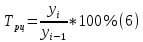 базисный: 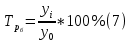 Темп прироста: цепной: 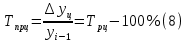 базисный: 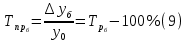 Среднегодовой темп роста исчисляется из отношения конечного и начального уровней ряда: 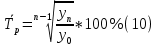 Среднегодовой темп прироста: 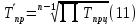 Таблица 4 - Результаты расчета основных показателей динамики
Средний уровень ряда динамики: 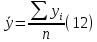 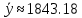 Среднегодовой темп роста 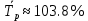 и прироста: и прироста: 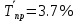 Прогнозные значения на следующие 12 месяцев представлены в таблице 5 и на графике (рисунок 3). Для полученных прогнозных значений рассчитаем отклонения от фактического значения и среднюю ошибку. Для прогноза, полученного с помощью среднего темпа роста 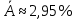 , для прогнозных значений, полученных с помощью среднегодового темпа прироста , для прогнозных значений, полученных с помощью среднегодового темпа прироста 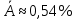 . Что говорит о высокой точности полученных значений. . Что говорит о высокой точности полученных значений.Таблица 5 – Расчет прогнозных значений с помощью среднего абсолютного прироста и среднего темпа роста
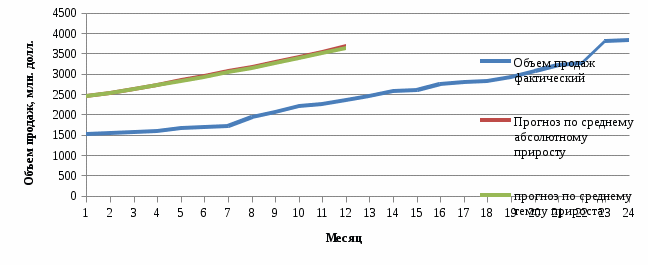 Рисунок 3 – График прогнозных значений с помощью среднего абсолютного прироста и среднего темпа роста | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
