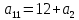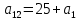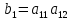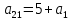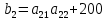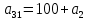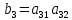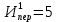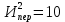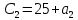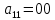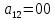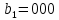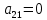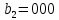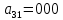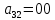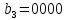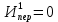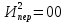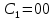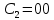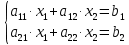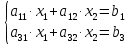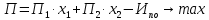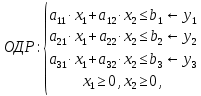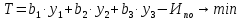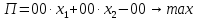Расчетно-графическая работа ЗЛП. РГР Задание. Задача линейного планирования
 Скачать 122.38 Kb. Скачать 122.38 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО «Чувашский государственный университет им. И.Н. Ульянова» Факультет прикладной математики, физики и информационных технологий Кафедра актуарной и финансовой математики Расчетно-графическая работа на тему «Задача линейного планирования» Вариант 00 Выполнил: студент группы ЗЭК-00-00 Фамилия И.О. Проверил: профессор каф. актуарной и финансовой математики Никитин В.В. Чебоксары 2021 Значения а1 первая, а2 вторая цифра номера по списку. Допустим, некоторое предприятия планирует производство двух видов изделий, используя три вида сырья. Нормы расхода сырья определены технологией производства и представлены в таблице. Данные о производстве и ожидаемой реализации изделий
Здесь 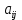 – количество сырья – количество сырья 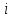 -го вида, используемого для производства одной единицы продукции -го вида, используемого для производства одной единицы продукции  -го вида. Запасы сырья -го вида. Запасы сырья  заданы. Они либо уже имеются, либо их планируют создать. Бухгалтерия совместно с технологическим отделом проводит учет всевозможных издержек, в частности, переменных издержек заданы. Они либо уже имеются, либо их планируют создать. Бухгалтерия совместно с технологическим отделом проводит учет всевозможных издержек, в частности, переменных издержек 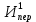 и и 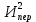 , и определяет будущие цены , и определяет будущие цены  и и 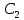 реализации одной единицы продукции. При этом реализации одной единицы продукции. При этом 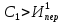 и и 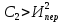 . . Каков должен быть в данных условиях план производства изделий, обеспечивающий в будущем при их реализации максимальную прибыль? При 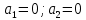
Требуется: Составить задачу линейного планирования (ЗЛП). Математической моделью для анализа заданной проблемы и ответа на поставленный вопрос является следующая задача линейного планирования   где П – прибыль; Д = (  · ·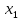 + + 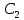 · · ) – доход; И= ( ) – доход; И= (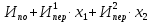 ) – общие издержки; ) – общие издержки; 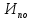 = = 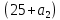 – постоянные издержки; – постоянные издержки; 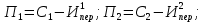 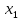 – количество планируемых к производству изделий первого вида; – количество планируемых к производству изделий первого вида; – количество планируемых к производству изделий второго вида; – количество планируемых к производству изделий второго вида;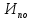 – постоянные издержки; – постоянные издержки;ОДР – область допустимых решений. Подставляя свои значения 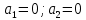 получаем: получаем: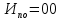 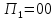  Для нашего варианта задача линейного планирования будет выглядеть так: 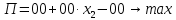 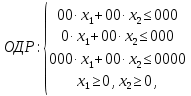 Данная математическая модель построена при допущениях: – весь объем производимых изделий будет реализован; – общие издержки производства линейно зависят от объемов производства. Решить ЗЛП графически. Определить (х1*, х2*) и Пmax = П(х1*, х2*) . 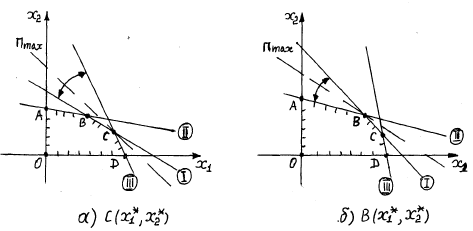 В одной половине вариант оптимальным решением будет точка С (ситуация а) ), а в другой точка В (ситуация б) ). Чтобы решить ЗЛП графически необходимо нарисовать систему пяти неравенств (полуплоскостей), которые определяют ОДР (область допустимых решений) в форме пятиугольника ОАВСD. Полуплоскости I, II, III отвечают следующим неравенствам системы 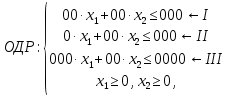 Граница полуплоскости будет прямая, уравнение которой получится, если вместо неравенства взять равенство. Затем границу полуплоскости I, II, III, т.е. прямую, можно нарисовать как обычно по двум точкам (задаем в уравнении прямой х1 и вычисляем х2 или наоборот). Первоначально можно нарисовать уравнение критерия 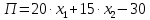 для произвольно заданного П. Тогда станет видно какая из точек даст крайнее положение критерия на границе ОДР. В нашем случае это будет точка О. Для расчета Пmax нужно знать координаты точки О. Её координаты находятся из решения системы для произвольно заданного П. Тогда станет видно какая из точек даст крайнее положение критерия на границе ОДР. В нашем случае это будет точка О. Для расчета Пmax нужно знать координаты точки О. Её координаты находятся из решения системы
В нашем случае оптимальным решением будет точка О с координатами (0,0 ; 0,0). Найдем максимальную прибыль, подставляя найденные координаты в уравнение критерия 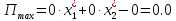 . .Рисунок для варианта 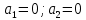 будет имеет вид: будет имеет вид: На рисунке прямая Пmax имеет уравнение критерия, где вместо П подставили Пmax . Найти интервал устойчивости оптимального решения. Пока прямая критерия остается в секторе, указанном двойной стрелкой на рисунке, найденное оптимальное решение останется оптимальным. Ситуация а) : точка С(х1*, х2*) остается оптимальным решением пока  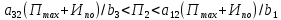 Ситуация б) : точка В(х1*, х2*) остается оптимальным решением пока 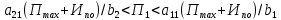  В нашем случае оптимальным решением является точка О. Подставляя свои значения получаем: 0,0 <  < 0,0 < 0,00,0 < 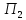 < 0,0 < 0,0Составить двойственную задачу и найти её оптимальное решение (теневую цену).
В соответствии с нашим вариантом будем иметь следующее соотношение задач
Ситуация а) : у2*=0 , то есть сырьё второго вида будет использовано не полностью при реализации оптимального решения С(х1*, х2*). Значения у1* и у3* находятся из решения системы 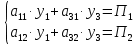 Ситуация б) : у3*=0 , то есть сырьё третьего вида будет использовано не полностью при реализации оптимального решения В(х1*, х2*). Значения у1* и у2* находятся из решения системы 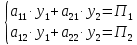 В данном варианте необходимо найти решение системы 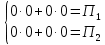 Решив систему можно записать оптимальное решение двойственной задачи 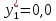  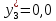 Подставляя найденные значения находим : 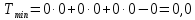 Проверка: Пmax = П(х1*, х2*) = Тmin = Т(у1*, у2*, у3*) = 0,0. Дополнительная единица сырья увеличивает максимальную прибыль на величину: Пmax(bi + 1) = Пmax(bi ) + уi* . Следовательно, сырье первого вида более ценное в смысле увеличения максимума прибыли, так как при увеличении этого вида сырья на одну единицу максимальная прибыль увеличится на 0,0. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||