Задача линейного программирования
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
|
Транспортная задача линейного программирования Оптимизация загрузки производственных мощностей предприятий по производству запасных частей для железнодорожного транспорта. Исходные данные: Производственные мощности предприятий вариант – 6(95:10=9ост.5+1=6)
Потребности в запасных частях. Вариант – 6 (95:6=15ост.5+1=6)
Размещение пунктов отправления и назначения на транспортной сети. Вариант – 4 (95:4=23 ост3+1=4)
Номера узлов размещения мощностей – индексы i: 1, 5 , 6, 11, 16. Номера узлов размещения потребителей – индексы j: 2 , 3, 7, 8, 9, 10, 12, 13, 14, 15. Решение: 1. Постановка задачи и формулировка экономико-математической модели. Железнодорожный транспорт в больших объемах потребляет разнообразные запасные части для поддержания активной части своих производственных фондов в работоспособном состоянии. Запасные части для предприятий железнодорожного транспорта изготавливаются на заводах по ремонту подвижного состава и производству запасных частей и других специализированных предприятиях. Снижение издержек, связанных с обеспечением предприятий железнодорожного транспорта запасными частями весьма актуально. Учитывая большую протяженность железных дорог России, эта задача должна решаться комплексно как для производственной, так и для транспортной составляющей затрат. Нам известно, сколько груза отправляется из каждого пункта и сколько груза должно поступить в пункт назначения. Причём безразлично, какой именно отправитель будет доставлять груз тому или иному получателю Требуется так организовать перевозки, чтобы обеспечить минимальный общий пробег груза, т. е. минимизировать затраты на транспортировку. Для решения этой задачи используем экономико-математическую модель транспортной задачи линейного программирования. В частности, ее разновидность – открытая модель транспортной задачи. Для построения экономико-математической модели рассматриваемой задачи введем следующие обозначения: аi – производственные мощности предприятий по производству запасных частей по пунктам размещения i; bj – потребности в запасных частях в пунктах j; xij – объемы перевозок запасных частей между пунктами производства и пунктами потребления i, j; Зi – затраты на производство единицы (удельные затраты) запасных частей у предприятий по пунктам i; сij – затраты на транспортировку единицы запасных частей между пунктами производства и потребления; аi' – загрузка производственных мощностей предприятий по производству запасных частей по пунктам размещения i. Тогда экономико-математическая модель может быть сформулирована следующим образом: найти совокупность переменных аi', минимизирующих целевую функцию F:  В данной задаче имеется пять предприятий по производству запасных частей и десять пунктов потребления, предполагается, что суммарная мощность всех предприятий должна превышать общие потребности. Это весьма важно, поскольку при равенстве задача оптимизации теряет смысл, так как будет возможен только один вариант решения при стопроцентной загрузке мощностей. Следовательно, имеет место открытая транспортная задача. Нереализованная продукция относится на счёт фиктивного потребителя. производственный мощность линейный программирование 2. Определение показателей производственных мощностей. Производственные затраты рассчитываем по формуле:  З1=40,5+  руб. руб.З2=40,5+  руб. руб.З3=40,5+  руб. руб.З4=40,5+ 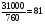 руб. руб.З5=40,5+  руб. руб.3. Расчет затрат на транспортировку единицы запасных частей между пунктами производства и потребления. По исходным данным строим схему рассматриваемого полигона железных дорог – транспортную сеть (рис.1). Далее выделяем узлы, в которых размещены производственные мощности и потребители запасных частей. Затем по сети рассчитываем кратчайшие расстояния между каждым пунктом производства и потребления. Результаты расчета заносим в таблицу 1. Расчет кратчайших расстояний между пунктами производства и потребления: А1 - В1: 110 км А1 – В2: 75 км А1 – В 3: 75+170=245 км А1 – В4: 75+130=205 км; А1 – В5: 130 км; А1 – В6: 110+130=240 км; Аналогично рассчитываем расстояния по каждому пункту потребления. А2 – В1: 150+160=310 км А2 – В2:150 км А2 – В3: 49+117=166 км А2 – В4: 130+117+79=326 км А2 – В5: 112 км Аналогично рассчитываем расстояния по каждому пункту потребления. А3 – В1: 69 км А3 – В2: 69+160=229 км А3 – В3: 125 км А3 – В4: 125+117=242 км А3 – В5: 125+117+100=342 км Аналогично рассчитываем расстояния по каждому пункту потребления. А4 – В1: 95+130=225 км А4 – В2: 135+170=305 км А4 – В3: 135 км А4 – В4: 135+117=252 км Аналогично рассчитываем расстояния по каждому пункту потребления. А5 – В1: 79+117+130=326 км А5 – В2: 79+105+135+170=484 км А5 – В3: 79+105+135=319 км А5 – В4: 79+105+150+95=429 км Рисунок 1 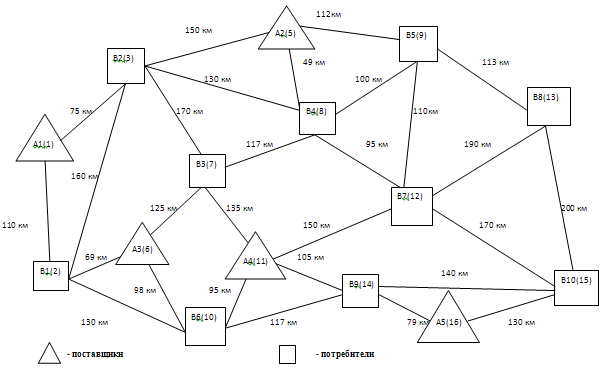 Таблица 1.
Затраты на транспортировку одной тонны запасных частей рассчитываем по формуле: где е – расходная ставка на 10 ткм. Для рассматриваемого рода груза принимается равной 4 руб.; L – минимальное расстояние, рассчитываемое для заданного полигона между пунктами производства и потребления, км. С11=4*110/10=44;С12=4*75/10=30;С13=4*245/10=98;С14=4*205/10=82; С15=4*337/10=135; С16=4*240/10=96; С17=4*300/10=120; С18=4*450/10=180; С19=4*357/10=143; С110=4*470/10=188. С21=4*310/10=124; С22=4*150/10=60; С23=4*166/10=66; С24=4*49/10=20; С25=4*112/10=45; С26=4*389/10=156; С27=4*144/10=58; С28=4*225/10=90; С29=4*399/10=160; С210=4*314/10=126. С31=4*69/10=28; С32=4*229/10=92; С33=4*125/10=50; С34=4*242/10=97; С35=4*342/10=137; С36=4*98/10=39; С37=4*337/10=135; С38=4*527/10=211; С39=4*215/10=86; С310=4*355/10=142. С41=4*225/10=90; С42=4*305/10=122; С43=4*135/10=54; С44=4*252/10=101; С45=4*260/10=104; С46=4*95/10=38; С47=4*150/10=60; С48=4*340/10=136; С49=4*105/10=42; С410=4*245/10=98. С51=4*326/10=130;С52=4*484/10=194;С53=4*319/10=128;С54=4*429/10=172; С55=4*443/10=177; С56=4*196/10=78; С57=4*300/10=120; С58=4*330/10=132; С59=49*79/10=32; С510=4*130=52. Результаты представлены в матрице:
Построение расчетной матрицы. Строим матрицу, отражающую особенности решаемой задачи. В процессе решения открытая модель транспортной задачи сводится к закрытой за счет балансировки ресурсов и потребностей. Для этого вводится фиктивный потребитель и ему назначается спрос, равный разнице суммарных мощностей и потребностей:  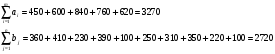 Затраты на транспортировку и производство запасных частей: 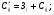 C11=109+44=153;С12=109+30=139;С13=109+98=207;С14=109+82=191; С15=109+135=244; С16=109+96=205; С17=109+120=229; С18=109+180=289; С19=109+143=252; С110=109+188=297. С21=92+124=216; С22=92+60=152; С23=92+66=158; С24=92+20=112; С25=92+45=137; С26=92+156=248; С27=92+58=150; С28=92+90=182; С29=92+160=252;С210=92+126=218. С31=77+28=105;С32=77+92=169;С33=77+50=127;С34=77+97=174; С35=77+137=214;С36=77+39=116;С37=77+135=212;С38=77+211=288; С39=77+86=163; С310=77+142=219. С41=81+90=171; С42=81+122=203; С43=81+54=135;С44=81+101=182; С45=81+104=185; С46=81+38=119; С47=81+60=141; С48=81+136; С49=81+42=123; С410=81+98=179. С51=91+130=221; С52=91+194=285; С53=91+128=219; С54=91+172=263; С55=91+177=268;С56=91+78=169;С57=91+120=211;С58=91+132=223; С59=91+32=123; С510=91+52=143. Матрица, отражающая особенности решаемой задачи, принимает вид: Транспортная таблица
По строкам матрицы отражены мощности по производству запасных частей. По столбцам отражены потребители и их спрос. В клетках матрицы, в маленьких квадратиках, представлены показатели критерия оптимальности модели – суммарные затраты на производство и транспортировку продукции между предприятиями и потребителями. В столбце фиктивного потребителя показатели критерия оптимальности приравниваются к нулю. Объемы перевозок между пунктами производства и потребления, которые находятся в результате решения, помещаются в клетки матрицы. Расчет оптимального плана транспортной задачи для расчетной матрицы. Сформулированная таким образом задача решается с помощью «Поиска решения» в MS Excel. Результаты решения транспортной задачи целесообразно представить в виде таблицы: Матрица поставок
F=367 550 руб. Расчет показателей оптимального плана загрузки производственных мощностей. Анализ результатов решения показывает следующее. Предприятие А1 оправляет реальному потребителю В2 - 410 т. запасных частей, а остальные 40 т приходятся на фиктивного потребителя. Это говорит о том, что мощности А1 востребованы не полностью. Следовательно, загрузка А1 составляет 410 т., т.е. 91%. Предприятие А2 отправляет предприятиям В4, В5 и В8 по 390, 100 и 110 т. соответственно, что в сумме составляет – 600 т. Мощности предприятия А2 полностью вошли в оптимальный план, следовательно загрузка А2 составляет 100%. То же самое имеет место и для предприятия А3. Потребители В1, В3 и В6 получают от данного предприятия по360, 230 и 250 т. соответственно, что сумме составляет 840 т. Иначе говоря, мощности предприятия А3 полностью вошли в оптимальный план, следовательно загрузка составляет 100% . Предприятие А4 поставляет потребителям В7 – 310 т., В8 –240 т., что в сумме составляет 550 т., а 210 т. запасных частей приходятся на фиктивного потребителя, следовательно мощности А4 востребованы не полностью и загрузка предприятия составляет 72,4%. Предприятие А5 отправляет реальным потребителям В9 - 250 т. и В10 – 100т. запасных частей, что в сумме составляет 350 т. Оставшиеся 300 т. не востребованы. Следовательно, загрузка предприятия А5 составляет 48,4%. Предприятия, которые не полностью используют производственную мощность, необходимо переориентировать на выпуск нового вида продукции или закрыть. Рассчитаем затраты в целом по оптимальному плану, в том числе на производство и транспортировку продукции: Производственные расходы: 410  109+600 109+600 92+840 92+840 77+550 77+550 81+350 81+350 91=240 970руб. 91=240 970руб.Транспортные расходы составляют: 367 550 -240 970=126 580 руб. Из данных расчетов следует, что на транспортную составляющую приходится 34,4% (126580*100/367550=34,4). Высокий удельный вес транспортной составляющей, свыше 5% свидетельствует о том, что транспортный фактор оказывает существенное значение на загрузку производственных мощностей для данной транспортной сети. Список литературы
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
