Математика ММУ. Задача Методом изоклин построить интегральные кривые уравнения
 Скачать 61.27 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Математика Группа Студент МОСКВА 2022 Задача 1. Методом изоклин построить интегральные кривые уравнения 1.1.  .Решение: Задавая различные значения параметра k, можно получить семейство кривых, каждая из которых является изоклиной при определённом значении параметра k. Построение изоклин - один из приёмов качественного анализа поведения решений анализируемого дифференциального уравнения. У нас  Это уравнения изоклин. При  получаем уравнение прямой  , при  получаем семейство гипербол с центром в точке (0;1). При  , при  .Построим график (изоклины (гиперболы для 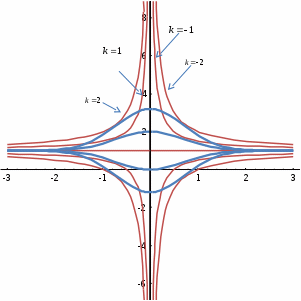 и  и прямая для k = 0) – красным цветом, интегральные кривые – синим): Задача 2. Решить уравнение, допускающее понижение порядка 2.1.  .Решение: Это дифференциальное уравнение 2-го порядка. Оно позволяет снизить его порядок путем подстановки  , потому что не содержит функцию у. Вторая производная:  . Тогда после подстановки  , где  . Это уравнение с разделяющимися переменными. Разделяем переменные: Þ  Þ  .Проинтегрируем обе части этого равенства:  Þ  Þ  Þ  .Возвращаемся к переменной у:  Þ получаем: ,  ,  .Переменные разделены. Интегрируем обе части равенства:    . - общее решение.Ответ: .Задача 3. Решить систему уравнений 3.1.  Решение: присвоим уравнениям системы номера (1) и (2). Сначала из уравнения (1) выражаем переменную  . Подставляем это выражение в уравнение (2), получаем:  Þ  Это уравнение с разделяющимися переменными. Разделяем переменные:  Интегрируем обе части:  , Þ  Þ  .Подставляем полученное выражение в уравнение (1):  . Разделяем переменные и интегрируем обе части:  Þ  Þ  , ,  .Тогда для функции  :  . Ответ: Общее решение системы имеет вид  .Задача 4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение: данная задача принадлежит к схеме испытаний Бернулли: Пусть проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью p и не происходит с вероятностью q = 1 – p. Наивероятнейшее число появлений события в схеме Бернулли находится из двойного неравенства:  .У нас  Þ  . Нужно найти число испытаний n, при котором наивероятнейшее число появлений события  = 10.Подставляем наши данные:  Þ  Þ Þ  Þ  Þ целое число, удовлетворяющее этому неравенству, равно  .Ответ: . |