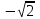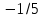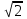Численные методы. 6 Теория погрешностей Понятие абсолютной и относительной погрешности, значащей и верной цифр
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
6.3. Теория погрешностей Понятие абсолютной и относительной погрешности, значащей и верной цифр. Ошибкой или погрешностью а приближенного значения а точного числаА называют разность 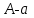 (иногда ею называют разность (иногда ею называют разность 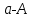 ). Абсолютную величину разности между точным и приближенным значением называют абсолютнойпогрешностью. Положительное число ). Абсолютную величину разности между точным и приближенным значением называют абсолютнойпогрешностью. Положительное число 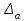 , удовлетворяющее неравенству , удовлетворяющее неравенству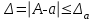 , ,называется предельной абсолютной погрешностью. И для оценки точного числа пользуются записью 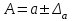 , где , где 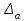 задает границы его неопределенности. задает границы его неопределенности.Относительной погрешностью называется величина 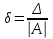 . Предельная относительная погрешность: . Предельная относительная погрешность: 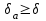 . Если для определенности положить . Если для определенности положить 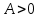 , , 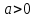 и и 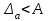 , то очевидно, что , то очевидно, что 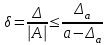 . Следовательно, выражение в левой части неравенства можно принять за предельную относительную погрешность . Следовательно, выражение в левой части неравенства можно принять за предельную относительную погрешность 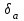 . Обычно . Обычно 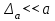 , в этом случае используют следующее приближение: , в этом случае используют следующее приближение: 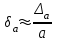 и и 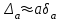 . .Рассмотрим пример, связанный с погрешностью округления. Определим, какое из двух равенств, представленных ниже, окажется точнее 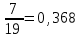 или или 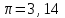 . .Значения в левых частях равенств найдем с большим числом десятичных знаков, откуда вычислим абсолютную погрешность. Она составляет соответственно 0,0004210… и 0,0015926… Сами погрешности (и абсолютные и относительные) принято округлять с избытком, так как при этом границы неопределенности числа, как правило, увеличиваются. Округляя с избытком, получаем предельные абсолютные погрешности 0,00043 и 0,0016 соответственно. Предельные относительные погрешности так же соответственно составляют 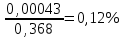 и и 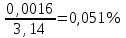 . В результате получаем, что второе равенство оказалось точнее. . В результате получаем, что второе равенство оказалось точнее.Кроме округления имеются другие источники погрешности: математическая модель, исходных данные, приближенный метод, погрешность машинных вычислений. При определении итоговой погрешности числа, погрешности, полученные от разных источников, складываются. Пользоваться оценкой 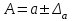 не всегда удобно. Так для физических констант и табличных данных границы неопределенности, как правило, не задаются, однако они всегда имеют определенную точность, связанную с понятиями значащей и верной цифры числа. не всегда удобно. Так для физических констант и табличных данных границы неопределенности, как правило, не задаются, однако они всегда имеют определенную точность, связанную с понятиями значащей и верной цифры числа.Значащими называют все цифры в записи числа, начиная с первой ненулевой слева. Например, в числе 0,042 значащими будут две цифры 4 и 2. Это же число можно записать, как 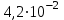 и в этой записи так же две значащие цифры. В числе 350,0 все цифры значащие, при записи его как 350 или и в этой записи так же две значащие цифры. В числе 350,0 все цифры значащие, при записи его как 350 или 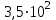 количество значащих цифр уменьшается и если изначально в числе определены четыре значащих цифры, то последние две его записи не правомерны. количество значащих цифр уменьшается и если изначально в числе определены четыре значащих цифры, то последние две его записи не правомерны.Значащая цифра называется верной в узком смысле, если абсолютная погрешность числа не превосходит половины единицы десятичного разряда, соответствующего этой цифре. Для числа 36,528, определенного с погрешностью 0,07 будут верными только цифры 3 и 6. Цифра 5 будет уже не верна, так как единица ее разряда это 0,1 а половина от этого значения меньше погрешности. Аналогично будут не верны цифры 2 и 8. В числах принято оставлять только верные цифры, пользуясь при этом пользуясь правилами округления. В предыдущем примере, если оставить только первые две цифры, округлив число до 37, то погрешность округления составит 0,472. Общая погрешность составит 0,472+0,07=0,542. Это означает, что вторая цифра числа оказалась не верной и округление нужно продолжить. Округлив число до 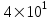 , получаем единственную верную цифру, погрешность числа в итоге составит 3,542. , получаем единственную верную цифру, погрешность числа в итоге составит 3,542.В некоторых случаях используют понятие верной цифры в широком смысле. Это означает, что абсолютная погрешность числа не превосходит единицы десятичного разряда, соответствующего этой цифре. Справочные величины, как правило, имеют в своем составе все верные цифры в широком смысле. И если, например, задана некоторая физическая константа 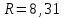 , то можно утверждать, что ее абсолютная погрешность не превышает 0,005. Данное значение можно принять за предельную абсолютную погрешность и вычислить предельную относительную погрешность: 0,005/8,31 6,02104 = 0,0602. Если округлить результат с избытком до одной значащей цифры, то погрешность составит 0,07. , то можно утверждать, что ее абсолютная погрешность не превышает 0,005. Данное значение можно принять за предельную абсолютную погрешность и вычислить предельную относительную погрешность: 0,005/8,31 6,02104 = 0,0602. Если округлить результат с избытком до одной значащей цифры, то погрешность составит 0,07.Погрешность математических выражений. При вычислении математических выражений, в которые входят приближенные числа, возникает необходимость в определении погрешности результата. Для этого нужно уметь вычислять погрешности арифметических операций и функций. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел. Если х1, х2, х3, …, х1n данные приближенные числа, а u – их алгебраическая сумма, то согласно теореме, 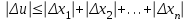 . .Вследствие этого за предельную абсолютную погрешность алгебраической суммы можно принять сумму предельных абсолютных погрешностей слагаемых 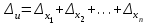 . .Данная формула используется, как при сложении, так и при вычитании. Относительная погрешность произведения (частного) приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел. Если x,y приближенные числа и 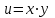 (аналогично при (аналогично при 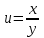 ), то, следуя предыдущей теореме, можно записать: ), то, следуя предыдущей теореме, можно записать: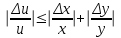 или или 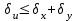 . .Таким образом, за предельную относительную погрешность произведения (частного) можно принять сумму предельных относительных погрешностей множителей (делимого и делителя). Нетрудно понять из предыдущих рассуждений, что за предельную относительную погрешность степени 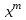 (где x – приближенное число) можно принять произведение показателя степени на предельную относительную погрешность основания (где x – приближенное число) можно принять произведение показателя степени на предельную относительную погрешность основания 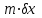 . .Рассмотрим пример вычисления погрешности выражения 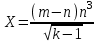 при 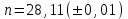 , , 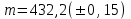 , , 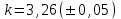 . .Вначале найдем X=5970441,129. Результат округлим до четырех значащих цифр: 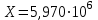 . За абсолютную предельную погрешность округления в этом случае можно принять . За абсолютную предельную погрешность округления в этом случае можно принять 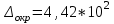 . .Заметим, что в скобках и в подкоренном выражении производится операция вычитания. В этом случае производится расчет с помощью абсолютных погрешностей. Имеем 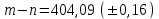 , , 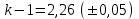 . .Переходя к относительным погрешностям можно записать итоговое выражение. 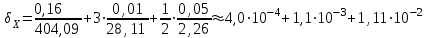 В итоге, округляя с избытком, получим 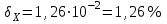 . .Предельная абсолютная погрешность 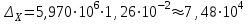 . .Если учесть погрешность округления, то окончательно можно записать: 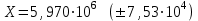 . .Для вычисления предельной абсолютной погрешности функции многих переменных: f(x1, x2,…,xn), каждая из которых является приближенным числом, справедлива формула: 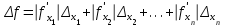  В частности, для функции от одной переменной: f(x) справедлива формула: 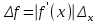 Например: 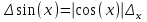 Вычисления без точного учета погрешностей. При массовых вычислениях обычно не учитывают погрешность каждого отдельного результата и в этих случаях пользуются следующими правилами подсчета верных цифр. При сложении и вычитании приближенных чисел в исходных данных для каждого числа определяют младший десятичный разряд. Среди младших разрядов чисел выбирают максимальный, а полученный результат сложения или вычитания округляют до этого разряда. Например, 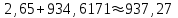 . .При умножении и делении в результате сохраняют столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр. При возведении в квадрат или куб (а также при извлечении квадратного и кубического корней) в результате оставляют столько значащих цифр, сколько их имеет основание степени (подкоренное выражение). Во всех промежуточных результатах оставляют на одну значащую цифру больше. У окончательного результата лишнюю цифру округляют. Ниже представлен пример вычислений без точного учета погрешностей. Пусть 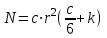 , где , где 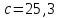 , ,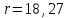 , , 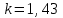 . .Тогда 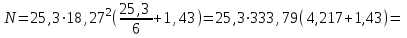 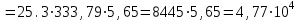 6.4. Методы решения нелинейных уравнений Отделение корней Дано уравнение вида 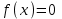 . Всякое значение , обращающее в нуль функцию f(x), называется корнем функции. Из-за сложного вида функции часто возникают трудности с аналитическим решением, и в этом случае пользуются вычислительными методами для приближенного нахождения корней. Корни требуется получить с заданной наперед точностью ε. . Всякое значение , обращающее в нуль функцию f(x), называется корнем функции. Из-за сложного вида функции часто возникают трудности с аналитическим решением, и в этом случае пользуются вычислительными методами для приближенного нахождения корней. Корни требуется получить с заданной наперед точностью ε.Приближенное нахождение действительных изолированных корней проходит в два этапа: 1) отделение корней, т.е. установление как можно более тесных промежутков, на которых содержится только один корень уравнения;2) уточнение приближенных корней с точностью ε. Существует два способа для отделения корней: графический и аналитический. В первом случае строится график функции и находятся точки пересечения с осью абсцисс. Часто сложную функцию f(x) разбивают на две h(x), g(x) таким образом, чтобы уравнение 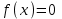 можно было заменить на можно было заменить на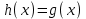 . В этом случае корень функции f(x) определяется из пересечения графиков двух вспомогательных функций. . В этом случае корень функции f(x) определяется из пересечения графиков двух вспомогательных функций.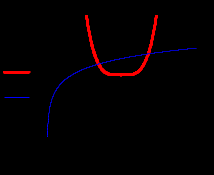 Пусть 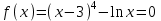 , тогда , тогда 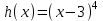 и и 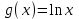 . .Из построенного с помощью системы MathCAD графика видно, что имеются два корня: при 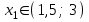 и и 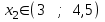 . .Для второго способа отделения корней используется следующая теорема (Больцано-Коши): Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. 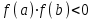 , то внутри этого отрезка содержится, по меньшей мере, один корень уравнения. Корень будет заведомо единственным, если производная f’(x) существует и сохраняет постоянный знак внутри интервала (а,b). , то внутри этого отрезка содержится, по меньшей мере, один корень уравнения. Корень будет заведомо единственным, если производная f’(x) существует и сохраняет постоянный знак внутри интервала (а,b).Рассмотрим аналитический способ отделения корней для следующего примера: 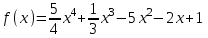 . Требуется найти участки, на которых производная . Требуется найти участки, на которых производная 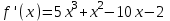 сохраняет знак. Для этого необходимо вычислить корни уравнения сохраняет знак. Для этого необходимо вычислить корни уравнения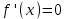 ). В промежутках между корнями знак производной сохраняется. Решая уравнение: ). В промежутках между корнями знак производной сохраняется. Решая уравнение: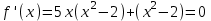 , находим три корня: , находим три корня: 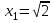 , , 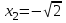 , , 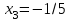 . Следовательно, имеются четыре интервала: . Следовательно, имеются четыре интервала: 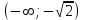 , , 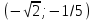 , , 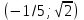 , , 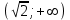 , на которых знак производной не меняется. Для определения промежутков, в которых содержаться корни функцииf(x), необходимо исследовать знак функции на концах интервалов. Результат такого исследования удобно представить в таблице: , на которых знак производной не меняется. Для определения промежутков, в которых содержаться корни функцииf(x), необходимо исследовать знак функции на концах интервалов. Результат такого исследования удобно представить в таблице:
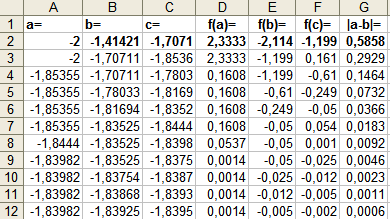
Из таблицы видно, что все четыре корня по одному находятся внутри отдельных интервалов. Промежутки отделения корней можно сузить путем подбора. При этом необходимо следить, чтобы на концах отрезка [a,b], внутри которого ищется корень, выполнялось бы неравенство f(a)f(b)<0. Так интервал 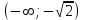 , можно заменить на интервал , можно заменить на интервал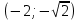 . Заметим, что если бы функция в точке –1/5 была отрицательна, то она имела бы всего два действительных корня в интервалах . Заметим, что если бы функция в точке –1/5 была отрицательна, то она имела бы всего два действительных корня в интервалах 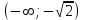 и и 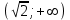 . Это означало бы, что у данной функции два других корня – комплексные. . Это означало бы, что у данной функции два других корня – комплексные.Методы уточнения корней Метод половинного деления (метод дихотомии) предназначен для уточнения значения корня на отрезке [a,b] с заданной точностью ε. Суть этого метода заключается в том, что сначала находится середина отрезка 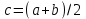 , затем определяется часть отрезка, [a,с] или [с,b], внутри которого располагается корень. Если f(a)f(с)<0 , то корень содержится внутри отрезка [a,с] и деление можно продолжить, приняв за правый конец точкус, выполнив присваивание b=c. В противном случае, когда f(с)f(b)<0, в точку с смещается левый конец отрезка: а=с. и т.д. Процесс половинного деления следует остановить, когда длина отрезка окажется меньше заданной точности: , затем определяется часть отрезка, [a,с] или [с,b], внутри которого располагается корень. Если f(a)f(с)<0 , то корень содержится внутри отрезка [a,с] и деление можно продолжить, приняв за правый конец точкус, выполнив присваивание b=c. В противном случае, когда f(с)f(b)<0, в точку с смещается левый конец отрезка: а=с. и т.д. Процесс половинного деления следует остановить, когда длина отрезка окажется меньше заданной точности: 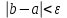 . Любая точка внутри такого отрезка – искомое решение. . Любая точка внутри такого отрезка – искомое решение.Ниже приведены результаты уточнение корня рассмотренной выше функции на интервале 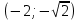 , с точностью , с точностью 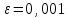 . .
использовать условную функцию «ЕСЛИ». В данном примере в ячейках третьей строкитаблицы записаны следующие формулы:
нижние строки заполняются с помощью копирования.
Методы Ньютона (касательных) и хорд Для численного решения уравнения 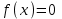 методами Ньютона и хорд необходимо, чтобы первая и вторая производные функции f(x) были непрерывны и сохраняли знак на отрезке [a,b], в котором заключен единственный корень . Из условия постоянства знака первой производной следует единственность корня при методами Ньютона и хорд необходимо, чтобы первая и вторая производные функции f(x) были непрерывны и сохраняли знак на отрезке [a,b], в котором заключен единственный корень . Из условия постоянства знака первой производной следует единственность корня при 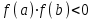 на заданном отрезке, а из условия постоянства знака второй производной следует, что выпуклость функции не меняется на вогнутость и наоборот. на заданном отрезке, а из условия постоянства знака второй производной следует, что выпуклость функции не меняется на вогнутость и наоборот. |