Численные методы. 6 Теория погрешностей Понятие абсолютной и относительной погрешности, значащей и верной цифр
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
6.6. Линейная аппроксимация по МНК Пусть зависимоcтьy от xзадана в дискретной форме: {x1, y1; x2,y2; … xn,yn}. По этим данным можно построить такую аппроксимирующую функцию, график которой будет располагаться между узлами интерполяции близко к ним, но не обязательно точно проходить через все узлы. Такая зависимость носит сглаживающий характер и строится, например, для того, чтобы описать экспериментальные данные с помощью функции заданного вида. Необходимо определить лишь параметры этой функции. Для решения такой задачи используется метод наименьших квадратов - МНК. Его суть заключается в минимизации полной квадратичной невязки между построенной функцией и значениями yiв узловых точках:  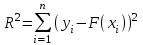 где F(x) – искомая аппроксимирующая функция. Часто в качестве приближения, строящегося по МНК, берутся полиномы степени l, 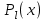 , где l<n-1. В простейшем случае строится полином первой степени, т.е. линейная функция: F(x)=ax+b. Коэффициенты a и b находятся с помощью метода наименьших квадратов по следующим формулам: , где l<n-1. В простейшем случае строится полином первой степени, т.е. линейная функция: F(x)=ax+b. Коэффициенты a и b находятся с помощью метода наименьших квадратов по следующим формулам: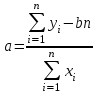 , , 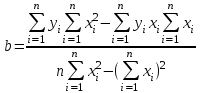 . .Для нахождения коэффициентов, можно использовать стандартные функции системы MathCAD и Excel. В MathCAD имеется функция line(vx, vy), которая возвращает линейные коэффициенты по значениям векторных аргументов vxи vy. В Excel имеется функция ЛИНЕЙН, у которой также имеются два аргумента, состоящих из диапазонов ячеек. На первом месте диапазон ячеек соответствующий ординате. После ввода этой функции (например, «=ЛИНЕЙН(F10:F12;E1:E3)» ) выводится только один линейный коэффициент. Для вывода обоих коэффициентов необходимо выделить две ячейки (включая первую слева) потом нажать «F2», а затем комбинацию клавиш «crtl», «shift», «enter». 6.7. Решение систем линейных уравнений (СЛУ) Систему линейных уравнений 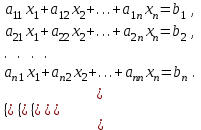 удобно представлять в матричной форме 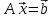 , где , где 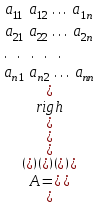 матрица системы, матрица системы, 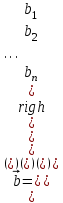 вектор столбец свободных членов. вектор столбец свободных членов.Система имеет единственное решение, если ее определитель 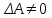 . Для решения системы используют прямые методы (формулы Крамера, метод Гаусса, метод обратной матрицы) и итерационные (метод простых итераций, Зейделя и др.). . Для решения системы используют прямые методы (формулы Крамера, метод Гаусса, метод обратной матрицы) и итерационные (метод простых итераций, Зейделя и др.).
Решение систем линейных уравнений с использованием стандартных функций пакета MathCAD и Excel.В пакете MathCAD имеется множество возможностей для решения СЛУ.
Решение системы в компактном виде осуществляется с использованием матрицы системы и вектора столбца свободных членов, а также с помощью функции lsolve.    Также можно воспользоваться методом обратной матрицы При решении СЛУ с помощью стандартных функций Excel требуется умение работы с массивами. Для решения, например, с помощью обратной матрицы используются функции МОБР и МУМНОЖ.
Для использования функции обращения матрицы МОБР нужно ввести в свободную ячейку формулу: «=МОБР(A1:C3)» или воспользоваться мастером функций, в котором отметить диапазон ячеек.
элементы,необходимо выделить соответствующе количество ячеек так, чтобы в левом верхнем углу находился полученный элемент. После этого нажимается клавиша «F2», а затем сочетание клавиш «crtl», «shift», «enter». В выделенных ячейках появится результат. Следующим шагом нужно перемножить обратную матрицу с вектором-столбцом свободных членов. При умножении в свободную ячейку вводится функция умножения с необходимыми диапазонами перемножаемых массивов «=МУМНОЖ(A6:C8;E1:E3)». После того как в ячейке появится первый элемент, необходимо выделить ячейки для результата (три столбиком, включая первый злемент), затем нажать «F2» и «crtl», «shift», «enter». Метод Гаусса Суть метода заключается в том, что сначала путем тождественных преобразований систему приводят к треугольному виду (прямой ход), а затем последовательно находят корни системы (обратный ход). Если из второй строки уравнения вычесть первую, умноженную на коэффициент 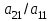 , а из третьей строки вычесть тоже первую, умноженную на коэффициент , а из третьей строки вычесть тоже первую, умноженную на коэффициент 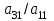 , и так продолжая до n-й строки, то в матрице преобразованной системы уравнений первый столбец, кроме элемента , и так продолжая до n-й строки, то в матрице преобразованной системы уравнений первый столбец, кроме элемента 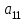 , станет нулевым. Элемент , станет нулевым. Элемент 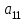 при данном преобразовании называется ведущим. Затем аналогичным способом, вычитая из нижних строк вторую, умноженную на соответствующие коэффициенты, зануляют второй столбец, кроме элементов при данном преобразовании называется ведущим. Затем аналогичным способом, вычитая из нижних строк вторую, умноженную на соответствующие коэффициенты, зануляют второй столбец, кроме элементов 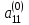 и и 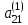 (верхний индекс обозначает количество преобразований), при этом преобразовании ведущим становится элемент (верхний индекс обозначает количество преобразований), при этом преобразовании ведущим становится элемент 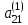 . Процесс продолжают, пока матрица А не примет треугольный вид: . Процесс продолжают, пока матрица А не примет треугольный вид:
Свободные члены при этих преобразованиях так же изменятся 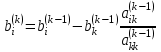 . .Из последней строки полученной матрицы находится 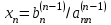 . . При выполнении описанных вычислений необходимо следить за тем, чтобы очередной ведущий элемент не был бы равен нулю. Если такое происходит, то следует производить перестановку строк. Так как в дальнейшем производится работа только с преобразованной матрицей, то верхние индексы можно опустить. Тогда из предпоследней строки 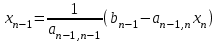 . .Полностью обратный ход можно записать: 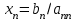 , , 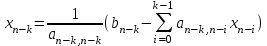 . .Рассмотренные преобразования не меняют определителя матрицы коэффициентов. Определитель же треугольной матрицы равен произведению элементов главной диагонали. Таким образом, с помощью метода Гаусса, можно найти определитель матрицы системы уравнений, вычислив произведение ведущих элементов. Ниже приведен пример решения системы уравненийс помощью метода Гаусса. 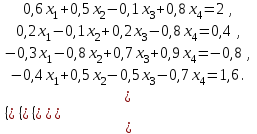
Произведение ведущих членов равно 0,1855 , что является значением определителя. |

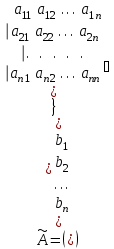 .
.


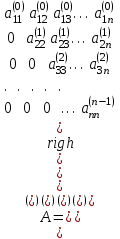 ,
,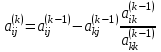 ,
, 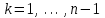 ,
, 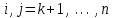 ,
,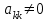 .
.