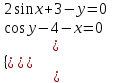Численные методы. 6 Теория погрешностей Понятие абсолютной и относительной погрешности, значащей и верной цифр
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Метод Ньютона (метод касательных). Имеется некоторое приближение xn точного значения корня . Тогда можно записать 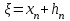 , где добавку hn считаем малой величиной. Используя разложение функции f(x) в ряд Тейлора около xnдо слагаемых первого порядка и приравнивая его к нулю, имеем: , где добавку hn считаем малой величиной. Используя разложение функции f(x) в ряд Тейлора около xnдо слагаемых первого порядка и приравнивая его к нулю, имеем: 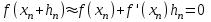 . Откуда . Откуда 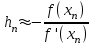 . . Так как добавка 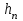 найдена приближенно, то можно сказать, что вычислено новое приближение xn+1 . Таким образом, получена итерационная формула найдена приближенно, то можно сказать, что вычислено новое приближение xn+1 . Таким образом, получена итерационная формула 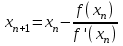 для для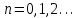 В качестве нулевого приближения x0выбирается тот конец отрезка [a,b], который удовлетворяет соотношению 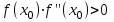 . .В общем случае, для оценки точности методом Ньютона недостаточно выполнения условия 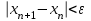 , однако оно становится применимым с ростом n(при , однако оно становится применимым с ростом n(при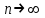 ). Оценить точность можно, пользуясь общей формулой ). Оценить точность можно, пользуясь общей формулой 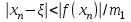 , где , где 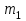 – наименьшее значение – наименьшее значение 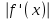 на отрезке [a,b]. на отрезке [a,b].Метод хорд.В методе хорд, в отличие от метода половинного деления, отрезок делится не пополам, а, что более естественно, пропорционально отношению 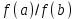 . Если для определенности принять . Если для определенности принять 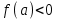 , , 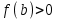 , а за х точку, в которой производится деление отрезка, то , а за х точку, в которой производится деление отрезка, то 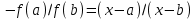 . После преобразований получается: . После преобразований получается: 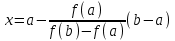 . После деления необходимо сдвинуть один из концов отрезка, так, чтобы корень оказался внутри нового отрезка. Неподвижным выбирается тот конец отрезка [a,b], который удовлетворяет соотношению . После деления необходимо сдвинуть один из концов отрезка, так, чтобы корень оказался внутри нового отрезка. Неподвижным выбирается тот конец отрезка [a,b], который удовлетворяет соотношению 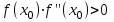 ,где ,где 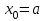 или или 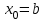 . В итоге итерационная формула для метода хорд принимает вид: . В итоге итерационная формула для метода хорд принимает вид: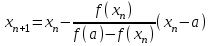 при при 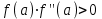 , ,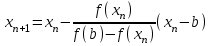 при при 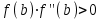 . .Итерации можно продолжать до тех пока 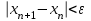 , это автоматически означает, что , это автоматически означает, что 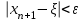 . .Ниже представлены примеры уточнения корня уравнения 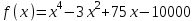 , определенного , определенного 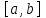 при при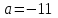 , ,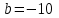 . .Так как 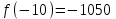 , ,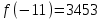 , а , а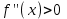 на на 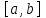 , то в качестве начальной точки для вычислений методом Ньютона необходимо выбрать , то в качестве начальной точки для вычислений методом Ньютона необходимо выбрать 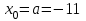 . Таблица вычислений с помощью метода Ньютона выглядит следующим образом: . Таблица вычислений с помощью метода Ньютона выглядит следующим образом:
Погрешность можно оценить из соотношения 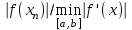 . Так как . Так как 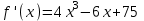 и на отрезке и на отрезке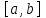 она монотонна, то она монотонна, то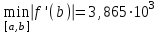 . .В итоге погрешность уточненного корня не превышает величины 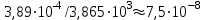 . .Для того, чтобы уточнить корень данного примера с помощью метода хорд, необходимо зафиксировать конец отрезка 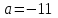 . Таблица вычислений этим методом: . Таблица вычислений этим методом:
Погрешность в этом случае можно оценить из разности двух последних приближений, или аналогично тому, как это было сделано ранее для метода Ньютона. Метод итерации. Суть этого метода заключается в том, что уравнение 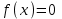 приводится путем тождественных преобразований к виду приводится путем тождественных преобразований к виду 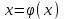 . Выбирая в области отделения корня начальное приближение x0, получают следующее приближение . Выбирая в области отделения корня начальное приближение x0, получают следующее приближение 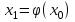 , затем вычисляют , затем вычисляют 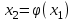 и т.д.. Таким образом, итерационная последовательность вычисляется по рекуррентной формуле: и т.д.. Таким образом, итерационная последовательность вычисляется по рекуррентной формуле: 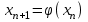 . Если процесс сходится, т.е. существует предел . Если процесс сходится, т.е. существует предел 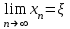 , то , то 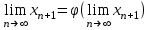 , откуда , откуда 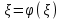 . Следовательно предельноезначение итерационнойпоследовательности является корнем исходного уравнения. . Следовательно предельноезначение итерационнойпоследовательности является корнем исходного уравнения.Теорема о сходимости метода итерации. Пусть 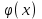 определена и дифференцируема на отрезке [a,b], тогда, если существует число q такое, что определена и дифференцируема на отрезке [a,b], тогда, если существует число q такое, что 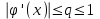 при при 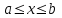 то: то:1) Процесс итерации 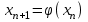 сходится независимо от начального значения сходится независимо от начального значения 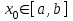 . .2) Предельное значение 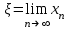 является единственным корнем уравнения является единственным корнем уравнения 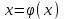 на отрезке [a,b]. на отрезке [a,b].При оценке достижения точностиε используется условие: 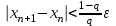 , где , где 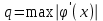 на отрезке [a,b]. В частности, при на отрезке [a,b]. В частности, при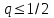 это условие можно заменить на более сильное неравенство это условие можно заменить на более сильное неравенство 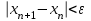 . .Для того, чтобы процесс сходился, 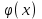 можно искать из соотношения можно искать из соотношения 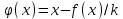 , где , где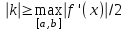 . kимеет тот же знак, что и . kимеет тот же знак, что и 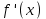 . .Производная 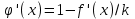 . Очевидно, что . Очевидно, что 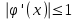 , так как отношение , так как отношение 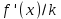 может принимать значения в диапазоне от нуля до двух. может принимать значения в диапазоне от нуля до двух.Решение уравнений с помощью стандартных функций MathCAD Кроме уже рассмотренной в начале раздела функции solve, решение уравнения можно получить с помощью функции root. Если исследуемая функция является полиномом, то все ее корни можно найти с помощью функции polyroots. Функция root может иметь два аргумента: root(f(x),x) или четыре аргумента: root(f(x),x, а,b). При использовании двух аргументов указывается сама функция f(x) и переменнаяx, относительно которой решается уравнение. Функция может иметь несколько корней, поэтому в случае использования двух аргументов необходимо указывать начальное (приближенное) значение. Когда используются четыре аргумента, два дополнительных aи bопределяют интервал, внутри которого находится корень. В последнем случае не требуется знать начального значения x, однако корень внутри заданного отрезка должен быть единственным, а значения f(а) и f(b) должны быть разных знаков. Ниже приведен пример вычисления корня ранее исследованной функции.
Решение системы двух нелинейных уравнений Дана система из двух нелинейных уравнений: 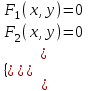 . .Точным решением системы (корнями) является пара чисел: 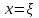 , , 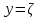 . .Отделение корней. Область, в которой находятся корни, можно определить графическим способом.
|

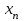
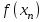
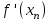
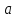
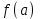
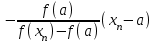
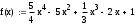


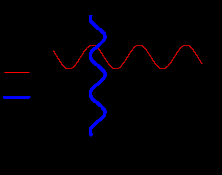
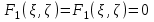 ) будут определять корни системы уравнений. Слева представлен график двух функций (построенный в системе MathCAD), с помощью которого определяются корни системы уравнений:
) будут определять корни системы уравнений. Слева представлен график двух функций (построенный в системе MathCAD), с помощью которого определяются корни системы уравнений: