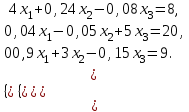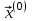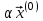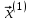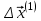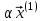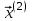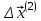Численные методы. 6 Теория погрешностей Понятие абсолютной и относительной погрешности, значащей и верной цифр
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Метод простых итераций Суть метода заключается в том, что исходную систему линейных уравнений приводят к эквивалентной системе вида: 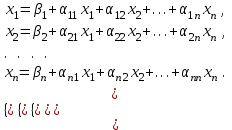 или или 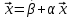 Взяв в качестве начального приближения вектор 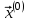 , получают следующее , получают следующее 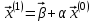 , затем , затем 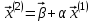 . В результате формула последовательных приближений имеет вид: . В результате формула последовательных приближений имеет вид: 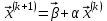 , , 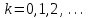 Метод сходится (независимо от выбора начального приближения), если любая из канонических норм матрицы меньше единицы. Рассмотрение условий 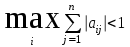 , , 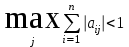 приводит к условию диагонального преобладания (в строках, или в столбцах) для исходной матрицы системы A. приводит к условию диагонального преобладания (в строках, или в столбцах) для исходной матрицы системы A.Итерационный процесс для решения системы с заданной точностью останавливается, если 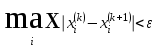 . . В следующем примере приводится решение СЛУ с помощью метода простых итераций.
выполнялось условие диагонального преобладания.Затем система приводится к виду необходимому для проведения итераций. 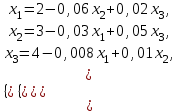 откуда откуда 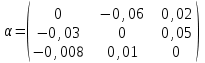 , , 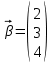 . .Ниже приведена таблица вычислений вектора решений 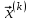 ( (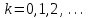 ). В качестве нулевого приближения взят вектор ). В качестве нулевого приближения взят вектор 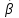 . Вычисления производились с точностью 0,001. Для этого норма вектора . Вычисления производились с точностью 0,001. Для этого норма вектора 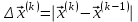 должна быть меньше единицы. должна быть меньше единицы.
Метод Зейделя Этот метод является модификацией метода итераций. Преобразованную систему 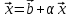 можно записать в следующем виде: можно записать в следующем виде: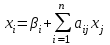 , i=1,…,n , i=1,…,nПолученное из перового уравнения системы приближение значение 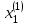 используется во втором уравнении для нахождения используется во втором уравнении для нахождения 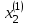 , затем оба значения , затем оба значения 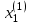 и и 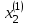 используются уже при нахождении используются уже при нахождении 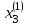 и т.д. Процесс повторяется для следующего приближения. В итоге можно записать и т.д. Процесс повторяется для следующего приближения. В итоге можно записать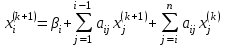 . .Условие сходимости, а также условие прекращения последовательных приближений для метода Зейделя аналогичны условиям для метода простых итераций. Необходимо отметить, что при вычислениях с помощью MathCAD, чтобы получить следующее приближение методом Зейделя, достаточно записать формулу 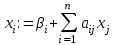 , так как для вычислений последующих компонент вектора , так как для вычислений последующих компонент вектора 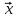 используются предыдущие (уже вычисленные) компоненты. используются предыдущие (уже вычисленные) компоненты. |