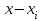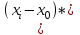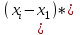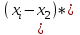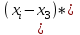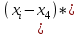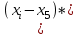Численные методы. 6 Теория погрешностей Понятие абсолютной и относительной погрешности, значащей и верной цифр
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Уточнение корней методом итераций. При решении системы уравнений методом итераций, она представляется в виде 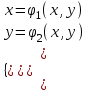 . Если за начальное приближение корней принять пару . Если за начальное приближение корней принять пару 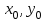 , то итерационный процесс выглядит, как: , то итерационный процесс выглядит, как: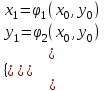 , , 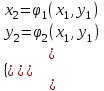 … … 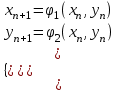 . .Если итерационный процесс сходится, т.е. существуют пределы 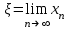 , , 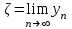 , то эти пределы являются решением исходной системы уравнений. , то эти пределы являются решением исходной системы уравнений.Для метода итераций справедлива следующая теорема: Пусть в некоторой замкнутой окрестности 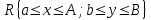 имеется одна (и только одна) пара корней имеется одна (и только одна) пара корней 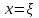 , , 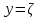 . Если: . Если: 1) функции 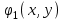 , , 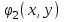 определены и непрерывно дифференцируемы, определены и непрерывно дифференцируемы, 2) начальные приближения 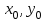 и все последующие приближения принадлежат окрестности R, и все последующие приближения принадлежат окрестности R, 3) в окрестности R выполняется условие 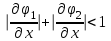 , , 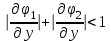 , ,то процесс итерации сходится. Уточнение корней методом Ньютона. Для удобства обозначений перепишем систему в виде: 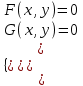 . Пусть . Пусть 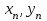 - приближенные значения корней системы при - приближенные значения корней системы при 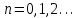 тогда для точных корней можно записать тогда для точных корней можно записать 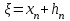 , , 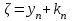 . Используя разложение Тейлора для функции многих переменных около . Используя разложение Тейлора для функции многих переменных около 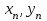 и ограничиваясь линейными слагаемымипо и ограничиваясь линейными слагаемымипо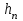 и и 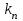 , запишем: , запишем: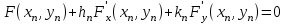 , , 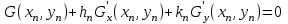 . .Если рассматривать эти уравнения, как систему линейных уравнений относительно 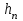 и и 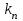 , то ее определитель , то ее определитель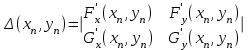 . .По правилу Крамера вычисляем: 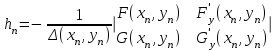 , , 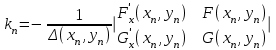  . .В итоге итерационные формулы принимаю вид: 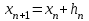 , , 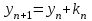 , , где 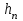 и и 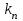 определяются предыдущими соотношениями. Итерационный процесс продолжается до выполнения условия: определяются предыдущими соотношениями. Итерационный процесс продолжается до выполнения условия: 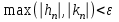 6.5. Интерполирование функций Постановка задачи В некоторой ограниченной области значений 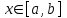 на плоскости (x,y) заданы n+1 точка: {x0, y0; x1,y1; … xn,yn}, (где xiрасположены в порядке возрастания) отражающие в дискретном виде функциональную зависимость y от x. Эти точки называются узлами интерполяции. Решить задачу интерполирования, это значит найти значение y(x) для промежуточных значений x. Задача интерполирования решается путем построения интерполяционной функции F(x), такой, что на плоскости (x,y) заданы n+1 точка: {x0, y0; x1,y1; … xn,yn}, (где xiрасположены в порядке возрастания) отражающие в дискретном виде функциональную зависимость y от x. Эти точки называются узлами интерполяции. Решить задачу интерполирования, это значит найти значение y(x) для промежуточных значений x. Задача интерполирования решается путем построения интерполяционной функции F(x), такой, что 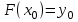 , , 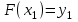 , … , , … ,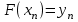 . Иначе говоря – проходящей через все узлы интерполяции. После этого искомое значение y(x) вычисляется как значение F(x). . Иначе говоря – проходящей через все узлы интерполяции. После этого искомое значение y(x) вычисляется как значение F(x).Если приближенное значение зависимости ищется за пределами области, т.е. при 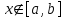 , то это называют экстраполирование. , то это называют экстраполирование.Полиномиальная интерполяция Если в качестве интерполяционной функции строится алгебраический многочлен – полином, то говорят о полиномиальной интерполяции. Согласно теореме единственности, через 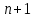 точку можно провести только один полином n-ой степени. Этот полином может иметь различную форму записи. Различают записи с помощью формул Ньютона и Лагранжа. точку можно провести только один полином n-ой степени. Этот полином может иметь различную форму записи. Различают записи с помощью формул Ньютона и Лагранжа.Полином Лагранжа. Наиболее общим вариантом интерполяционного полинома является полином Ланранжа. Он может быть получен при переменном шаге по x между узлами интерполяции. Не допускается лишь совпадение x-координат узлов. Для построения интерполяционного полинома Лагранжа используется базис, составленный из полиномов n-ой степени: 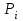 (x) (i=0,n), удовлетворяющих условиям: (x) (i=0,n), удовлетворяющих условиям: 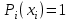 ; ; 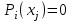 при при 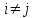 . Pi(x) имеет следующий вид: . Pi(x) имеет следующий вид: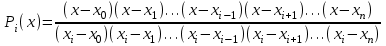 . .Интерполяционный полином Лагранжа 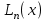 строится в виде: строится в виде: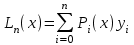 , ,Нетрудно показать, что он проходит через все узлы интерполяции: 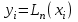 . .Полином можно записать в общем виде: 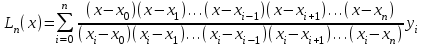 . .Иногда его записывают как 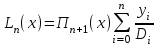 , где , где 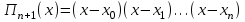 , ,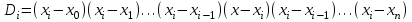 . .
П
роизведение последнего столбца таблицы дает 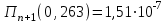 .Вычисление .Вычисление 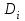 приведено ниже. приведено ниже.Окончательно 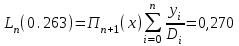 . .В случае равноотстоящих узлов интерполяционную формулу Лагранжа можно преобразовать к следующей форме: 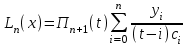 , , где 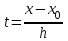 , , 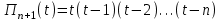 , , 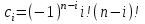 . .Интерполяционные полиномы Ньютона. Полиномиальная интерполяция по Ньютону производится при равноотстоящих по x узлах интерполяции. Первая интерполяционная формула Ньютона строится в виде: 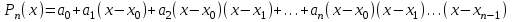 , ,где коэффициенты 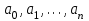 определяются из соотношения определяются из соотношения 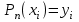 , ( , (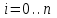 ). ).При нахождении коэффициентов используется понятие конечной разности. Для функции 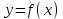 : : 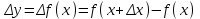 первая конечная разность, первая конечная разность,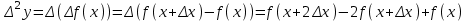 вторая конечная разность. В узловых точках имеем: вторая конечная разность. В узловых точках имеем: 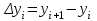 , , 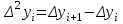 . .Аналогично для конечных разностей высших порядков 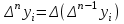 . .Итоговая формула, которая называется первой интерполяционной формулой Ньютона (в случае равноотстоящих узлов) имеет вид: 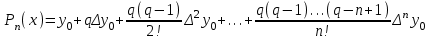 , ,где 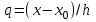 , h шаг (расстояние между соседними точками). При малых q членами высоких порядков в формуле можно пренебречь, поэтому первую формулу Ньютон обычно используют в случае, когда x близка к х0. , h шаг (расстояние между соседними точками). При малых q членами высоких порядков в формуле можно пренебречь, поэтому первую формулу Ньютон обычно используют в случае, когда x близка к х0.Ниже в таблице приведен пример таблично заданной функции и ее конечных разностей (до третьего порядка). Используя данную таблицу и формулу Ньютона (ограничиваясь членами третьего порядка по q) можно вычислить функцию, например, в точке 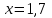 . .
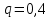 , , 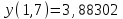 . .Примечание. При вычислениях, в качестве х0 лучше выбирать ближайшую точку к х. Например, для точки 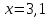 удобней выбрать удобней выбрать 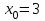 , тогда соответственно , тогда соответственно 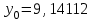 , , 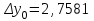 … …При вычислениях значений функции, близких к концу таблицы, первая формула Ньютона может оказаться мало пригодной из-за того, что члены высоких порядков велики и их нельзя сократить. В этом случае используют вторую формулу Ньютона, которая получается, если полином искать в виде: 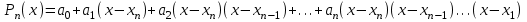 Вторая интерполяционная формула Ньютона имеет вид: 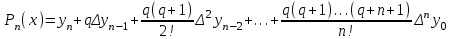 , ,где 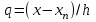 . .Вычислим функцию в точке 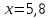 , тогда , тогда 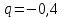 , , 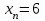 , , 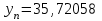 , , 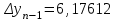 , , 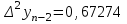 … … и, в результате (с точностью до третьего порядка по q) 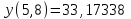 . .Сплайн интерполяция Сплайн функция сплайн кусочно-полиномиальная функция, проходящая через заданное множество узлов интерполяции и имеющая в данной области некоторое количество непрерывных производных. В вычислительной практике распространено использование кубических сплайнов. Приближение функции 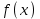 с помощью кубического сплайна с помощью кубического сплайна 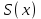 должно удовлетворять следующим условиям: 1) должно удовлетворять следующим условиям: 1) 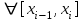 функция функция 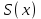 многочлен третьей степени; 2) функции многочлен третьей степени; 2) функции 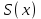 , , 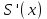 , , 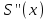 непрерывны на заданном отрезке непрерывны на заданном отрезке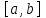 ; 3) ; 3) 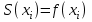 , согласно условию интерполирования. , согласно условию интерполирования.Для любого 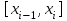 задается функция задается функция 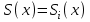 в виде многочлена третьей степени: в виде многочлена третьей степени: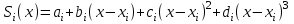 , ,где 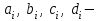 коэффициенты, подлежащие определению. коэффициенты, подлежащие определению.С учетом выше перечисленных условий, а так же двух дополнительных (для концов заданного отрезка) 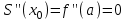 , , 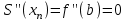 , коэффициенты записываются: , коэффициенты записываются: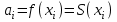 , , 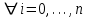 ; ;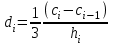 , , 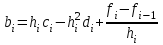 , , 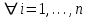 ; ;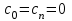 , ,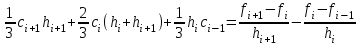 , , 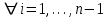 . .Здесь 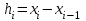 , , 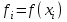 . .В образованной системе уравнений, коэффициенты 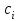 можно определить из последней строки методом прогонки. Остальные коэффициенты выражаются через найденные. Рассмотрим метод прогонки для нахождения коэффициентов можно определить из последней строки методом прогонки. Остальные коэффициенты выражаются через найденные. Рассмотрим метод прогонки для нахождения коэффициентов 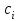 . Последнее уравнение системы это уравнение (при . Последнее уравнение системы это уравнение (при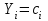 ) вида: ) вида: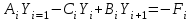 , , 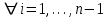 , ,где 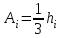 , , 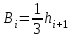 , , 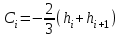 , , 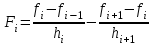 . .Если привести это уравнение к виду: 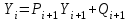 , , 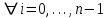 , то , то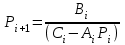 , , 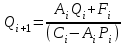 , , 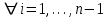 . .В двух последних строках заключена суть метода прогонки: сначала находятся все коэффициенты 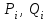 (необходимо знать (необходимо знать 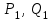 ), затем находятся значения ), затем находятся значения 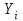 (необходимо знать (необходимо знать 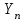 ). Так как ). Так как 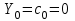 , а , а 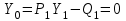 , то , то 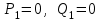 . С другой стороны . С другой стороны 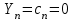 . .Ниже приведен пример вычисления коэффициентов полинома для функции заданной таблично. Этот же пример использован при рассмотрении полиномиальной интерполяции Лагранжа.
Сначала вычисляются прогоночные коэффициенты.
Затем вычисляются коэффициенты 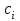 , и все остальные коэффициенты полинома. , и все остальные коэффициенты полинома.
Для того, чтобы вычислить функцию 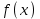 в точке в точке 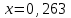 , необходимо вычислить полином , необходимо вычислить полином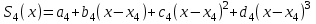 в этой точке. в этой точке.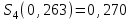 , что с точностью до трех знаков после запятой совпадает с раннее вычисленным значением по интерполяционной формуле Лагранжа. , что с точностью до трех знаков после запятой совпадает с раннее вычисленным значением по интерполяционной формуле Лагранжа. Ниже этот же пример решен с помощью системы MathCAD.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||