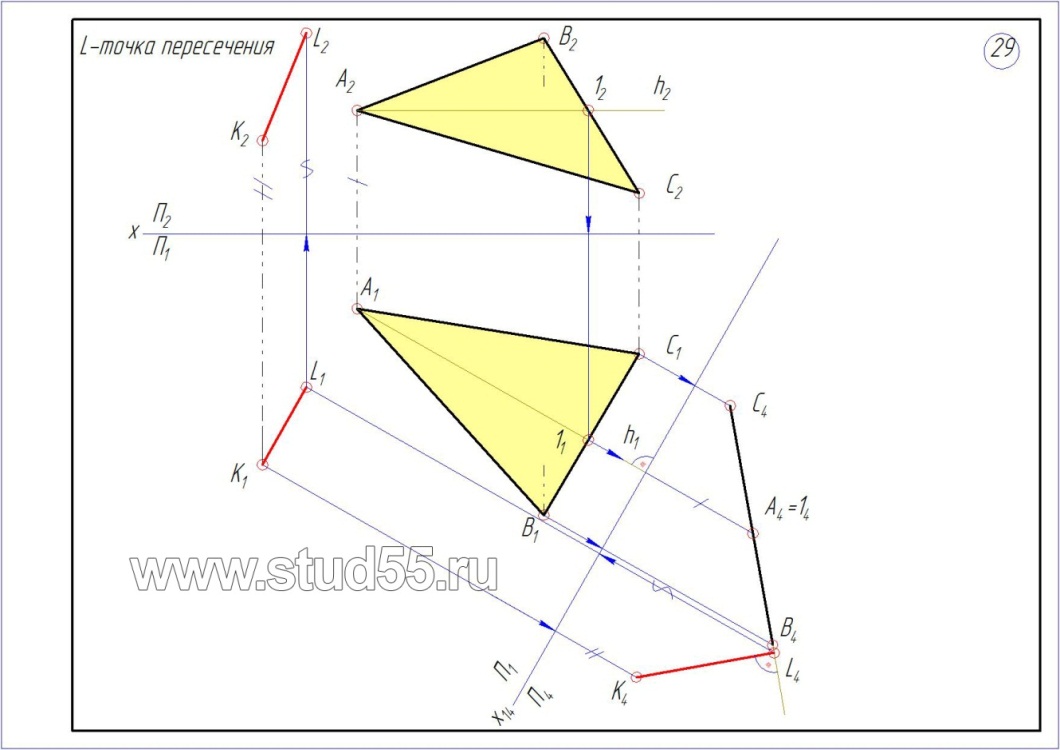
Расстояние между двумя параллельными прямыми. Задача может быть решена плоскопараллельным перемещением, вращением вокруг главной линии или двукратной заменой плоскостей проекций

• Название: Задача может быть решена плоскопараллельным перемещением, вращением вокруг главной линии или двукратной заменой плоскостей проекций
• Дата: 10.03.2022
• Размер: 0.83 Mb.
• Имя файла: Расстояние между двумя параллельными прямыми.docx
• Тип: Задача; #391064

Расстояние между двумя параллельными прямыми.

Задача может быть решена  плоскопараллельным перемещением, вращением вокруг главной линии или двукратной заменой плоскостей проекций.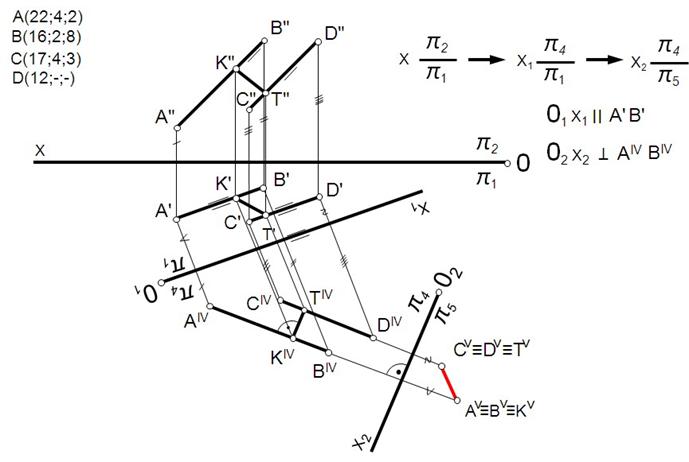



  Рис 120

Расстояние между двумя скрещивающимися прямыми. Задача может быть решена плоскопараллельным перемещением или двукратной заменой плоскостей проекций.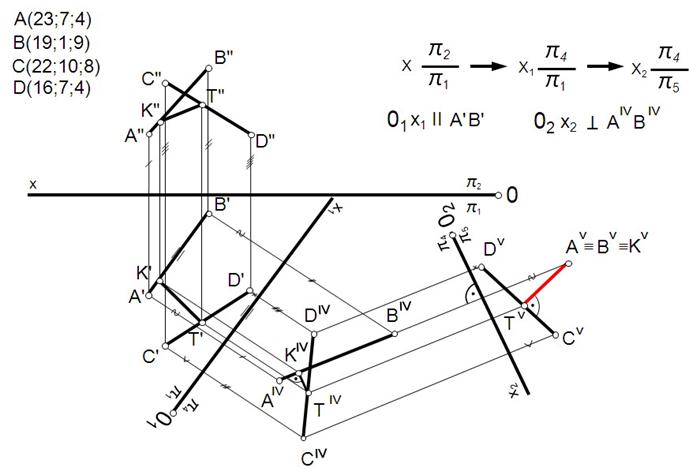



Рис 121

Расстояние между двумя параллельными плоскостями. Определяется длинной перпендикуляра, опущенного из произвольной точки одной плоскости на другую.

Задача. Даны скрещивающиеся прямые АВ и CD. Определить угол между ними 

(рис. 9.3).

Проекционное решение этой задачи, в соответствии с предложенной выше схемой, будет следующим:

1) строится ось проекции x1 // C1D1 (x1 можно строить параллельно любой из

 четырех ортогональных проекций прямых АВ и CD), которая вместе с 

 плоскостями П1 , П4 образует новую систему плоскостей проекций, такую, что

 П4 // CD;

2) на П4 строятся дополнительные проекции А4В4 , C4D4 прямых АВ и CD, при этом

 C4D4 есть НВ отрезка CD;

3) строится ось проекции x2 ^ C4D4 , которая вместе с П4 , П5 образует новую

 систему плоскостей проекций, такую, что П5 ^CD;

4) на П5 строятся дополнительные проекции А5В5 и C5 = D5 прямых АВ и CD;

5 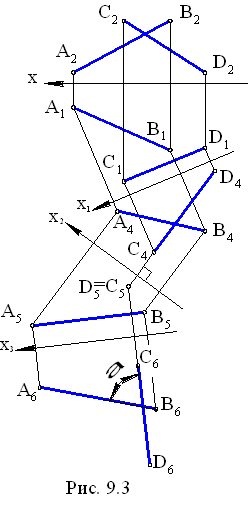) строится ось проекции x3 // А5В5 , которая

 вместе с П5, П6 образует новую систему

 плоскостей проекций, такую, что П6 // AB;

6) на П6 строятся дополнительные проекции

 А6В6 и C6D6 , представляющих собой НВ

 прямых АВ и CD и образующих между собой

 гол a, являющийся решением задачи.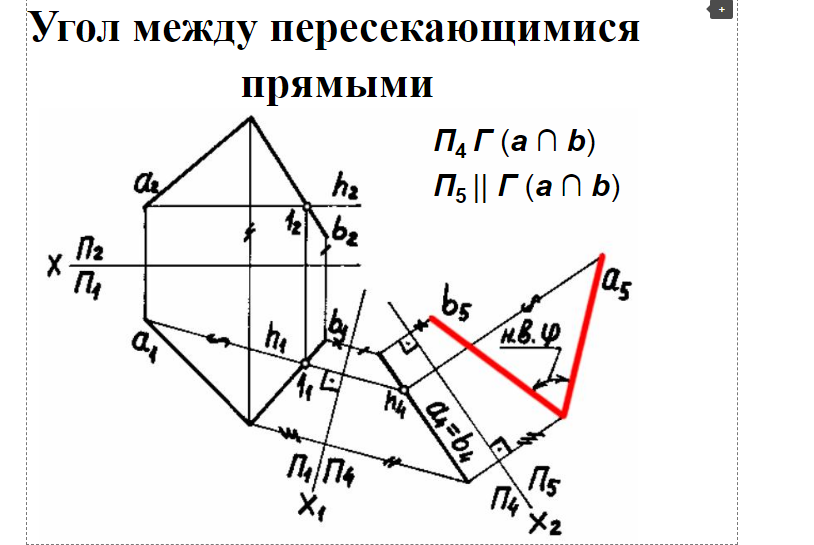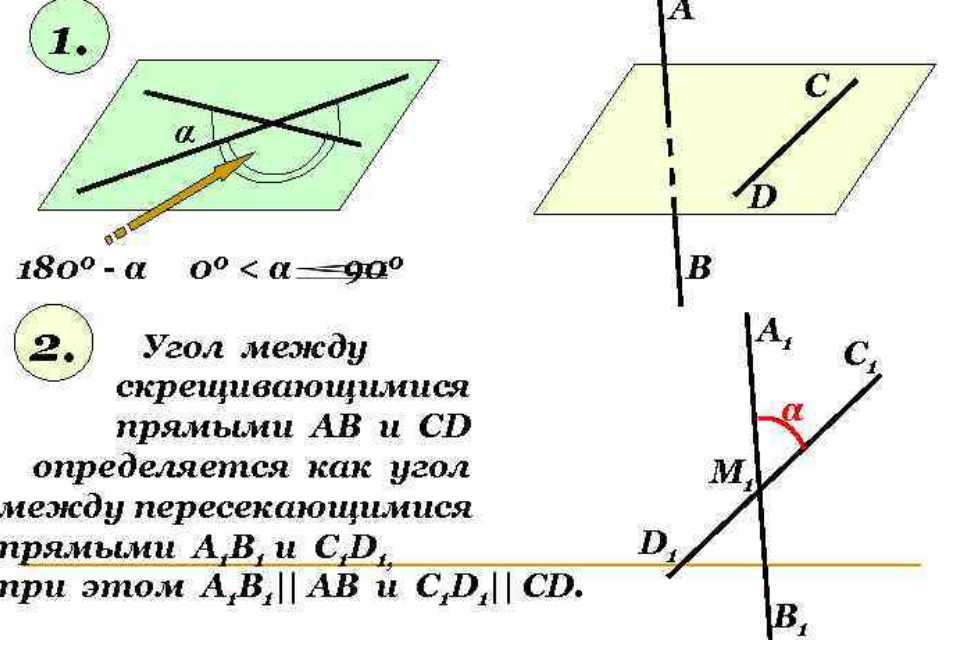

 

 

 

 

 



Угол между скрещивающимися прямыми

Измеряется углом между пересекающимися прямыми, параллельными данным скрещивающимся прямым.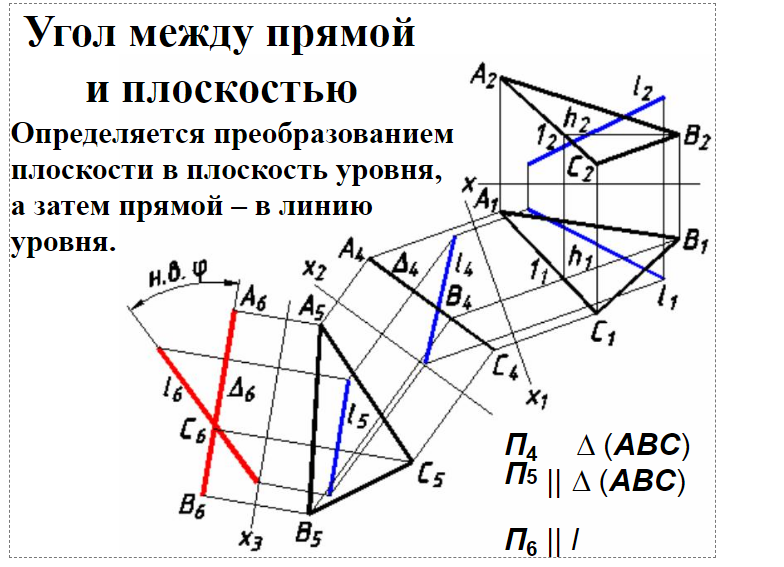


Использование способа замены плоскостей проекций для решения метрических и позиционных задач.

Задача №29 Определить расстояние от точки K до плоскости треугольника ABC

Решение:

Задача. Даны скрещивающиеся прямые АВ и CD. Определить угол между ними 

(рис. 9.3).

Проекционное решение этой задачи, в соответствии с предложенной выше схемой, будет следующим:

1) строится ось проекции x1 // C1D1 (x1 можно строить параллельно любой из

 четырех ортогональных проекций прямых АВ и CD), которая вместе с 

 плоскостями П1 , П4 образует новую систему плоскостей проекций, такую, что

 П4 // CD;

2) на П4 строятся дополнительные проекции А4В4 , C4D4 прямых АВ и CD, при этом

 C4D4 есть НВ отрезка CD;

3) строится ось проекции x2 ^ C4D4 , которая вместе с П4 , П5 образует новую

 систему плоскостей проекций, такую, что П5 ^CD;

4) на П5 строятся дополнительные проекции А5В5 и C5 = D5 прямых АВ и CD;

5 ) строится ось проекции x3 // А5В5 , которая

 вместе с П5, П6 образует новую систему

 плоскостей проекций, такую, что П6 // AB;

6) на П6 строятся дополнительные проекции

 А6В6 и C6D6 , представляющих собой НВ

 прямых АВ и CD и образующих между собой

 гол a, являющийся решением задачи.