итоговая по математике. ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА. Задача Найти матрицу, обратную матрице. Ответ Найдем определитель (детерминант) матрицы
 Скачать 33.67 Kb. Скачать 33.67 Kb.
|
|
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА Задача 1. Найти матрицу, обратную матрице 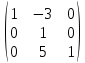 . . Ответ: Найдем определитель (детерминант) матрицы. Определитель матрицы равен 1 поэтому обратная матрица существует. Найдём её. Найдем минор M11 и алгебраическое дополнение A11. В матрице А вычеркиваем строку 1 и столбец 1 M11= 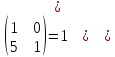 A11=(-1)1+1 · M11 = 1 · 1 = 1 Найдем минор M12 и алгебраическое дополнение A12. В матрице А вычеркиваем строку 1 и столбец 2. M12= 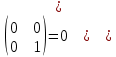 A12=(-1)1+2 · M12 = -1 · 0 = 0 Найдем минор M13 и алгебраическое дополнение A13. В матрице А вычеркиваем строку 1 и столбец 3. M13= 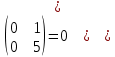 A13=(-1)1+3 · M13 = 1 · 0 = 0 Найдем минор M21 и алгебраическое дополнение A21. В матрице А вычеркиваем строку 2 и столбец 1. M21= 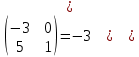 A21=(-1)2+1 · M21 = -1 · (-3) = 3 Найдем минор M22 и алгебраическое дополнение A22. В матрице А вычеркиваем строку 2 и столбец 2. M22= 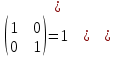 A22=(-1)2+2 · M22 = 1 · 1 = 1 Найдем минор M23 и алгебраическое дополнение A23. В матрице А вычеркиваем строку 2 и столбец 3. M23= 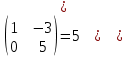 A23=(-1)2+3 · M23 = -1 · 5 = -5 Найдем минор M31 и алгебраическое дополнение A31. В матрице А вычеркиваем строку 3 и столбец 1. M31= 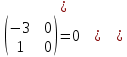 A31=(-1)3+1 · M31 = 1 · 0 = 0 Найдем минор M32 и алгебраическое дополнение A32. В матрице А вычеркиваем строку 3 и столбец 2. M32= 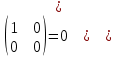 A32=(-1)3+2 · M32 = -1 · 0 = 0 Найдем минор M33 и алгебраическое дополнение A33. В матрице А вычеркиваем строку 3 и столбец 3. M33= 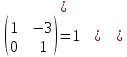 A33=(-1)3+3 · M33 = 1 · 1 = 1 Выпишем союзную матрицу (матрицу алгебраических дополнений): 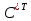 = =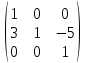 Транспонированная союзная матрица (поменяем местами строки со столбцами): 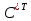 = =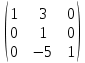 Найдем обратную матрицу: 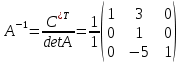 Сократим дробь: 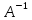 = = 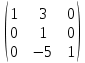 Задача 2. Решить СЛАУ 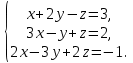 Общее решение: 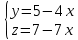 или или 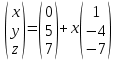 . .Задача 3. Вероятность того, что в результате проверки изделию будет присвоен «Знак высшего качества», равна 0,2. На контроль поступило 9 изделий. Какова вероятность того, что знак высшего качества будет присвоен: а) ровно 6-ти изделиям; б) более чем 7-ми изделиям; в) хотя бы одному изделию; г) указать наивероятнейшее число изделий, получивших знак высшего качества, и найти соответствующую ему вероятность. Решение. Вероятность того, что изделию не будет присвоен знак «изделие высшего качества» равна а) б) в) событие событие Тогда г) Наивероятнейшее количество изделий у нас получилось 1 или 2, значит их вероятности равны. Найдем |
