курсовая. Задача нелинейного программирования отличается от задачи на условный экстремум наличием дополнительных ограничений, имеющих вид
 Скачать 71.84 Kb. Скачать 71.84 Kb.
|
      Содержание. Содержание.Введение………………………………………………………………………..3 Глава1. Основы нелинейного программирования…………………………..4
Глава 2. Решение задачи нелинейного програмирования………………....23 Заключение …………………………………………………………………..25 Список литературы…………………………………………………………..26 Введение Данная работа направлена на исследование и решение задач нелинейного программирования. Актуальность данной темы состоит в том, что задачи нелинейного программирования встречаются в естественных науках, технике, экономике, информатике, математике, в сфере деловых отношений и в науке управления государством. Цель курсовой работы заключается в изучении одного из основополагающих разделов теории экстремальных задач – математическому программированию. Для осуществления обозначенной цели служат следующие задачи:
1.Основы нелинейного программирования Задача нелинейного программирования отличается от задачи на условный экстремум наличием дополнительных ограничений, имеющих вид h(x) <0, (1) где h: Rn →Rr- некоторая заданная функция, и называемых ограничениями типа неравенств. Поэтому ограничения g(x) = 0, (2) гдеg: Rn→Rm, в задаче нелинейного программирования называются ограничениями типа равенства. Таким образом задача нелинейного программирования заключается в минимизации числовой функции ƒ:Rn →R при выполнении ограничений (1) и (2). Задачу нелинейного программирования часто записывают в следующем виде: ƒ(x) → min, gi (x) = 0, i = 1,…..,m, (3) hi (x) <0, I = 1,……,r, объединяя тем самым функцию ƒ, подлежащую минимизация и ограничения (1) и (2), которые следует учитывать при выполнении минимизации. Как и в случае задачи на условный экстремум нелинейного программирования представляет интерес только в случае, когда n>m, что и предполагается в дальнейшем. При этом множество Q точек, для которых выполнены условия (1) и (2) замкнуто, т.е. если множество Q ограничено. 1.1Теорема Каруша – Джона В качестве примера будем рассматривать данные задачи. Задача (1) о минимизации функции ƒ (x1, x2) = - (x1)2 -(x2)2 при ограничении x1 + x2 = 1. Задача (2) о минимизации функции ƒ (x1, x2) =x1при ограничении (x1)2 + (x1)2 = 0. Пусть Q1 = {x€ Rn :gi(x) = 0, i = 1,…., m} – множество точек, для которых выполнены ограничения типа равенств (1), и пусть Q2 = {x€ Rn:hi(x) < 0, i = 1,…., r} – множество точек, для которых выполнены ограничения типа неравенств (2). Пересечение Q = Q1 ∩Q2 множествQ1иQ2дает точки x € Rn, называемые допустимыми точками в задаче (1). Точкаx*€Qназывается точкой минимума (или точкой локального минимума) в задаче (1), если для всех x€Q1, достаточно близких к допустимой точке x*1выполнено неравенство ƒ(x*) < ƒ(x). Необходимое условие минимума в задаче (3) дает следующая важнейшая для теории экстремальных задач. Теорема (Каруш – Джон). Пусть x*- точка минимума в задаче (2) и функции ƒ, g1,….,gmи h1,….,hrнепрерывно дифференцируемы в некоторой окрестности E точки х*. Тогда найдутся такие действительные числа 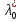 , , 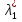 ,….., ,….., 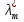 , и , и 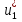 ,….., ,….., 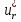 , не все равные нулю одновременно, что , не все равные нулю одновременно, что 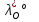 ƒ(х*) + ƒ(х*) +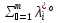 gi(x*) + gi(x*) + 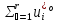 hi(x*) = 0,(4) hi(x*) = 0,(4)где 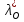 > 0 > 0и 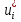 > 0, i = 1,……,r. > 0, i = 1,……,r.Доказательство. Пусть ε – некоторое положительное число и пусть U – множество точек x€ Rn, для которых |x – x*| <ε. Выберем число ε столь малым, чтобы все функции ƒ, g1,……, gmи h1,…., hr были непрерывно дифференцируемы на множестве Q ∩ U ⸦ E, причем каждая из функций h1,….,hr не меняла знак на множестве U∩(Rn\Q). Далее, пустьM – подмножество множества индексов i = 1,….,r, таких, что hi (x) > 0 на замыканииR множестваU ∩ (Rn\Q). Если множество M пусто, то теорема 3 справедлива, поскольку здесь можно принять 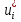 = 0, i = 1,…,r. = 0, i = 1,…,r.Исключив этот тривиальный случай, наряду с задачей (1) введем в рассмотрение задачу о минимизации функции ƒk :Rn→R, задаваемой равенством 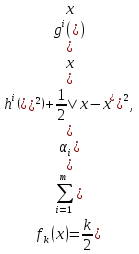 (5) где k – некоторое натуральное число, а a1,…., ar– действительные числа, задаваемые равенством 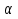 i= i=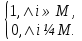 Функция ƒk, очевидно, непрерывна, а множества R – компактно. Поэтому ƒk для всех значений kимеет на множестве Rрешение xk, т.е. существует такоеxk∈R, что ƒk(xk) ≤ ƒk(x*). Отсюда в силу равенства (5) имеем 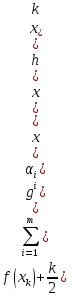 или, что эквивалентно, 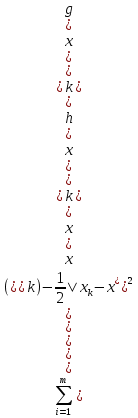 Поскольку для всех значений k = 1, 2,3,……. |xk -x*| < ε, то 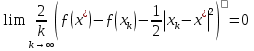 . .Следовательно, 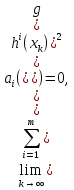 т. е. 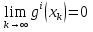 , i = 1,…..,m , i = 1,…..,mи 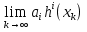 = 0, I = 1,……,r. = 0, I = 1,……,r.Выберем некоторую неограниченно возрастающую последовательность k1, k2,….., ki,….., 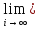 ki= ki= 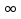 натуральных чисел. Легко видеть, что последовательность xk1, xk2,.., xki,..(6) ограничена. При этом gi( 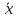 ) = 0, i = 1,..,m, ) = 0, i = 1,..,m,aihi ( 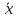 ) = 0, i = 1,..,r ) = 0, i = 1,..,rи ƒ ( 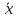 ) + ) +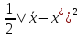 < ƒ (x*). (7) < ƒ (x*). (7)Поскольку х* - точка минимума на Q, то ƒ (x*) <ƒ ( 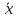 ). ).Поэтому из неравенства следует, что ( 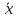 ) = x*, ) = x*,т. е. предельная точка всякой последовательности вида (3) совпадает с точкой х*. Следовательно, 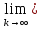 хk= х*, хk= х*,т. е. для всех достаточно больших значений k точка хk лежит внутри множества U. Но на множествоU 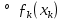 = 0 = 0или, что эквивалентно, 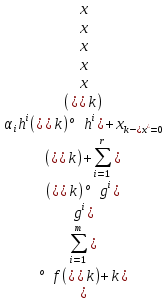 (8) Положим 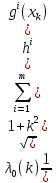 , ,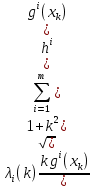 , ,i= 1,…..,m и 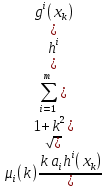 , ,i= 1,….,r. Тогда равенство (4) можно переписать в следующем эквивалентном виде: 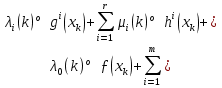 + +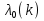 (xk–x*)= 0. (5) (9) (xk–x*)= 0. (5) (9)Поскольку, очевидно 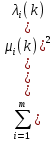 Для всех значений k = 1,2,3,……, то существует такая неограниченно возрастающая последовательность k1, k2,……, kj…., 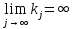 (10) (10)Натуральных чисел, что 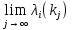 = = 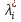 , i = 1,…., m , i = 1,…., mи 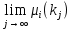 = = 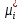 , i = 1,…., r, , i = 1,…., r,где 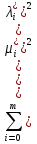 Поэтому, переходя в равенстве (5) к пределу при k 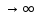 вдоль множества (1), в котором по построению вдоль множества (1), в котором по построению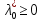 и 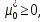 i = 1,….., r. i = 1,….., r.1.2Условия дополняющей нежесткости При доказательстве теоремы 1 использовался тот факт, что в точке х* минимума некоторые из ограничений типа неравенств обращаются в равенства, а некоторые другие – в строгие неравенства. Чтобы ясно различать указанные два возможных случая, введем следующие определение. Предположим, что при некотором значении i =1,…., rимеет место равенство hi(x*) = 0. Тогда будем говорить, что ограничение hi активно. Аналогичным образом, если при некотором значении j = 1,….,r имеет место не равенство hi(x*)< 0, то будем говорить, что ограничение hi активно. Обозначим через I* - множество активных ограничений в задаче (1) I*={i: hi(x*) = 0, i = 1,...,r} Просматривая доказательства теоремы 1, несложно заметить, что если i 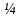 I, то I, то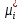 = 0. = 0.Если же i∈I*, то по определению hi(x*) = 0, т. е. в любом случае 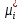 hi(x*) = 0, i = 1,…., r.(11) hi(x*) = 0, i = 1,…., r.(11)Равенство (11) называется условиями дополняющей нежесткости и используются следующем образом. Легко видеть, что условие (4) дает n уравнений относительно n + m + r + 1 неизвестного x*, 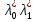 ,….., ,….., 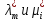 ….., ….., 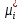 . Дополнив условие (4) уравнениями . Дополнив условие (4) уравнениямиgi (x*) = 0 i = 1,……., m и (11), получим систему n + m + rуравнений относительно n + m + r + 1 неизвестного x*, 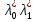 ,….., ,….., 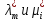 ….., ….., 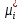 . При этом по прежнему велик соблазн принять . При этом по прежнему велик соблазн принять 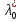 = 1(12) = 1(12)и, таким образом, замкнуть систему. Последнее, как и в случае задачи на условный экстремум, можно делать далеко не всегда, даже если ограничения типа равенств отсутствуют. Таким образом, условия дополняющей нежескости позволяют привести необходимое условие минимума в задаче (1). Чтобы замкнуть эту систему, нужно получить условия, позволяющие, например, наверняка принять равенство (12). Замечание. Необходимо отметить, что в условиях теоремы 3 принципиальным является следующий момент: либо 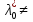 0, (13) 0, (13)либо 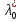 = 0. = 0.Последнее, конечно, объясняется тем, что множители 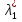 ,….., ,….., 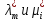 ….., ….., 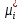 определены с точностью до неотрицательного множителя определены с точностью до неотрицательного множителя 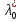 и потому при выполнении условия (13) без какой-либо потери общности можно принять равенство (12). и потому при выполнении условия (13) без какой-либо потери общности можно принять равенство (12).1.3Условие регулярности Для получения некоторых условий, гарантирующих справедливость условия (13) или, что эквивалентно, (12), введем в рассмотрение функцию 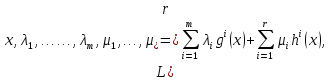 (14) которую будем называть функцией Лагранжа.При этом множители λ1,…..,λm, μ1,……., μr будем называть множителями Лагранжа. Принимая очевидные обозначения, перепишем равенство (14) в следующем эквивалентном виде: L(x,λ,μ) = ƒ(x) + 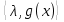 + + 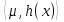 . .Если условие (14) выполняется, то в силу теоремы 3 необходимое условие минимума в задаче дает равенство 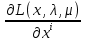 = 0, i = 1,……,n, = 0, i = 1,……,n,которое совместно с условиями g(x) = 0 и  = 0, i = 1,……..,r = 0, i = 1,……..,rобразуют замкнутую систему, решение которой дает искомые значения переменны. Условия, при которых справедливо равенство (12), принято называть условием регулярности. Простейшее из условий регулярности, которое будем называть первым условием регулярности, выглядит следующим образом: если х* - точка минимума в задаче (1), то функция ƒ,gmμhi,…..,hr непрерывно дифференцируемые в некоторой ее окрестности, а вектора 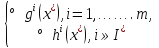 (15) (15)линейно независимым. Теорема 4. Пусть в некоторой точке х* выполнено первое условие регулярности. Тогда найдутся такие λ*∈ ℝmиμ* ∈ ℝr, что 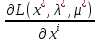 = 0, i = 1,…..,n(16) = 0, i = 1,…..,n(16)и 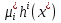 = 0, i = 1,…..,r, (17) = 0, i = 1,…..,r, (17) где 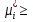 0. 0.Доказательство. Прежде всего, заметим, что условие (17) есть условие дополняющей нежесткости и выполняется в точке х* всегда. Далее, для всех i∉I* запишем 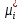 = 0. = 0.Тогда, поскольку вектора (15) линейно независимы, то в силу теоремы 3 следует принять 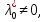 например, 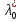 = 1, = 1,откуда и следует равенство (16). Замечание. Легко видеть, что первое условие регулярности полностью аналогично условию регулярного минимума в задаче на условный экстремум. Другими словами, теорема 4 является очевидным аналогом теоремы 2. При этом следует иметь ввиду, что проверку линейной независимость векторов (15) необходимо проделывать в точке минимума (заранее неизвестной) со всеми вытекающими отсюда последствиями. Все это, однако, не снижает исторической ценности теорем 2 и 4, поскольку именно с них собственно и начиналось математическое программирование. Сформулируем теперь более тонкое условие, которое будем называть вторым условием регулярности: если х* - точка минимума в задаче (1), то функции ƒ, gi,…..,gmиhi,…..,hrнепрерывно дифференцируемы в некоторой ее окрестности, вектора 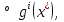 ……., ……., 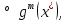 линейно независимы и существует такой вектор s∈ℝn, что линейно независимы и существует такой вектор s∈ℝn, что = 0, i = 1,……,m = 0, i = 1,……,mи 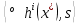 <0, i∈I*. <0, i∈I*.Замечание. Легко видеть, что геометрически второе условие регулярности означает следующие. В точке х* найдется элемент s касательного пространства к ограничениям типа равенств, который направлен внутрь каждого из множеств h*(x*) <0, i∈ I* активных в этой точки ограничений. Теорема 5. Пусть в некоторой точке х* выполнено второе условие регулярности. Тогда найдутся такие λ*∈ ℝm и μ* ∈ ℝr, что 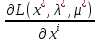 = 0, i = 1,…..,n (18) = 0, i = 1,…..,n (18)и 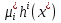 = 0, i = 1,…..,r, (19) = 0, i = 1,…..,r, (19) где 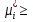 0. 0.Доказательство. Как и в случае теоремы 4, заметим, что условие (19) выполняется в точке х* всегда. Далее, для всех 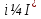 положим положим 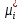 = 0. = 0.Тогда, предположим, что 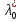 = 0. = 0.и умножаем равенство 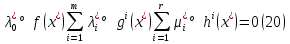 скалярно на s, получим 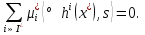 Отсюда в силу условий 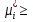 0. и 0. и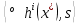 <0, i∈I* <0, i∈I*имеем 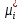 = 0. i = 1,…..,r. = 0. i = 1,…..,r.Поэтому равенство (20) принимает вид  где в силу теоремы 3 не все  одновременно равны нулю. Это, однако, противоречит принятой линейной независимости векторов одновременно равны нулю. Это, однако, противоречит принятой линейной независимости векторов g1(x*),…., gm(x*) и, значит, 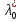 = 1, = 1,откуда и следует равенство (18). Замечание. Теорема 5, вообще говоря, выглядит мало привлекательно для практического использования. Однако из этой теоремы можно получить очень сильное небольшое условие минимума одного важнейшего класса экстремальных задач, в котором помимо условия регулярности будет автоматически выполнятся и достаточное условие минимума. 1.4Существование и единственность минимума. В отличии от задачи на условный экстремум, в задаче нелинейного программирования (1) достаточно просто устанавливаются условия существования решения. Объясняется это следующим. Легко видеть, что множества ограничений как в задаче на условный экстремум, так и в задаче (1) замкнуты. При этом в случае задачи на условный экстремум даже в простейших ситуациях множества Q допустимых точек не ограничено. Это приводит к тому, что вопрос о существовании решения задачи на условный экстремум часто остается открытым. В случае задачи нелинейного программирования (1) дело обстоит несколько иначе: добавление к ограничению (1) ограничения (2) часто приводит к тому, что множество Q допустимых точек становится ограниченным и, следовательно, компактным. Поэтому задача (1) обычно находится в условиях применяемости теоремы Вейерштрасса и, значит, вопрос о существовании ее решения часто снимается. Часто касается единственности решения задачи (1), то этот вопрос является гораздо более тонким. Как уже отмечалось ранее, в силу теоремы 4 и 5 точкой минимума может быть только точка х ∈Q, удовлетворяющая системе 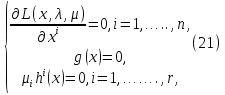 где неизвестным наряду с х является 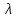 и μ, причем и μ, причем µi ≥0.(22) Тогда, если система (21) имеет единственное решение, удовлетворяющее условию (22), то в силу теорем 4 и 5 это решение будет единственной точкой минимума в задаче (1). На практике, однако, единственность решений системы (21) имеет место далеко не всегда, даже если минимум единственный. Последнее, например, объясняется тем, что решение системы (21) не обязано удовлетворять условию (22). Замечание. Необходимо отметить, что непосредственное применение к системе (21) какой-либо классической теоремы существования и единственности, очевидно, затруднено условием (22). Пример. Рассмотрим задачу о минимизации функции ƒ(х1, х2) = (х1)2 + (х2)2(23) при ограничениях х1 + х2 = 1, (24) х1> 0 (25) x2> 0. (26) Положим g(x1,x2) = x1 + x2 – 1, h1(x1, x2) = -x1 и h2(x1, x2) = -x2. Тогда, поскольку для всех значений х1 и х2 g(x1, x2) = (1,1), h1(x1, x2) = (-1, 0) и h2(x1, x2) = (0, -1), то заметив, что только одно из ограничений (25) или (26) может быть активным, видим, что для задачи (13) - (26) будет выполнятся первое условие регулярности. Поэтому без какой-либо потери общности можно принять L(x1, x2, λ, μ1, μ2) = (x1)2 + (x2)2 + λ(x1 + x2 -1) + μ1(-x1) + μ2(-x2). В силу теоремы 4 уравнения (21) для рассматриваемой задачи примут вид  (27) (27)где μ1>0, μ2>0. (28) Легко видеть, что при выполнении условия (28) система (27) имеет единственное решение 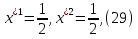 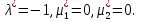 При этом, как несложно заметить, множество, задаваемое соотношениями (24) – (26), компактно, поскольку представляет собой отрезок прямой (24), заключенный между точками (0,1) и (1,0). Следовательно, точка (29) является точкой минимума в задаче (23) – (26). Пример. Рассмотрим задачу о минимизации функции 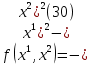 при ограничениях (24) – (26). Действуя, как и в примере 5, положим 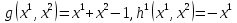 и 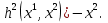 Тогда, поскольку для всех значений х1 и х2 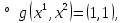 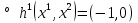 и  то заметив, что только одно из ограничений (25) или (26) может быть активным, видим, что для задачи о минимизации функции (30) при ограничениях (24) – (26) будет выполнятся первое условие регулярности. Поэтому без какой-либо потери общности можно принять 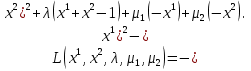 В силу теоремы 4 уравнения (21) для рассматриваемой задачи примут вид 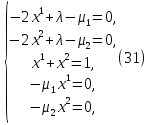 где μ1>0, μ2>0. (32) Легко видеть, что при выполнении условия (32) система (31) имеет решения x*1 = 0, x*2 = 1, λ* = 2,  x*1 = 1, x*2 = 0, λ* = 2,  и 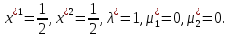 При этом, как уже отмечалось в примере 5, множество (24) – (26) Представляет собой отрезок прямой (24), заключенный между точками 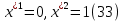 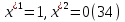 Следовательно, задача о минимизации функции (30) при ограничениях (24)-(26) имеет по крайней мере одно решение, т. е. по крайней мере одна из точек (33), (34) или  является точкой минимума. На самом же деле несложно заметить, что каждая из точек (33) и (34) является точкой локального минимума, а точка (35) – точкой локального максимума. 2.Решение задачи нелинейного программирования x2 + (y-11)2 x + y = 1 x + y – 1 = 0 x ≥ 0 - x < 0 y > 0 - y < 0 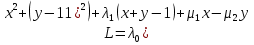 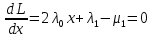 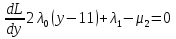 x + y – 1 = 0 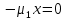 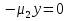 x x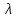 0 = 0 = 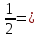 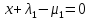
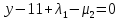 x + y – 1 = 0 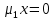 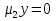 1. x = 0, y = 0 x + y = 0, невозможный случай
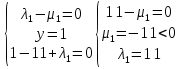
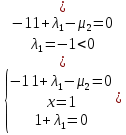
x+y=1 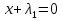 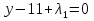 x =-  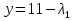 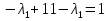 2 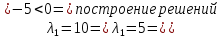 И так 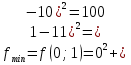 Ответ: 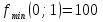 Заключение. Таким образом, изучив все материалы и применили их на практике, можно сказать, что цель работы достигнута. Ознакомились и изучили один из основополагающих разделов теории экстремальных задач – математическое программирование. Так же решили задачу нелинейного программирования. Список литературы 1.Элементарное введение в теорию экстремальных задач. А.П. Афанасьев, С.М. Дзюба М.: Наука, 1982. |

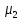 = 0
= 0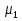 = 0
= 0