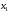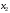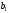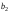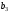Главная страница
Навигация по странице:

  • Решение задач ЛП в Excel

  • Загрузка надстроек Поиск решения и Анализ данных

  • Пример 1

  • Пример 2

  • Пример 3 (

    		•

    ЭММиМ. Задача об использовании ресурсов. Для изготовления двух видов продукции р 1, р 2 используются три вида ресурсов S


    Скачать 0.79 Mb.
    НазваниеЗадача об использовании ресурсов. Для изготовления двух видов продукции р 1, р 2 используются три вида ресурсов S
    Дата13.05.2023
    Размер0.79 Mb.
    Формат файлаdocx
    Имя файлаЭММиМ.docx
    ТипЗадача
    #1126158
    страница2 из 5
    1   2   3   4   5

    Статус ресурса (дефицитным или недефицитным) устанавливается в зависимости от того, полное или частичное их использование предусматривает оптимальное решение задачи. Если ограничение является связывающим, то этот ресурс относится к дефицитному (используется полностью). Если ограничение является не связывающим, то ресурс относится к недефицитному, следовательно, ресурсы 1, 3 являются дефицитными, а ресурс 2 - недефицитным.

    Решение задач ЛП в Excel

    Решение задач линейного программирования можно произвести с помощью надстройки MS Excel «Поиск решения». Надстройка становится доступной при установке MS Excel. Однако, чтобы использовать эту надстройку в Excel, необходимо сначала загрузить ее.

    Загрузка надстроек Поиск решения и Анализ данных:

    • в Microsoft Office 2010 щелкните значок Кнопка MicrosoftOffice , а затем Параметры Excel;

    • выберите команду Надстройки, а затем в поле Управление – пункт Надстройки Excel;

    • нажмите кнопку Перейти;

    • в окне Доступные надстройки установите флажок Поиск решения и нажмите ОК.

    После загрузки надстройки Поиск решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения.

    До вызова Поиск решения необходимо подготовить данные для решения

    задачи ЛП на рабочем листе Excel.

    Пример 1. Решим задачу ЛП.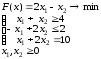



    Анализ данных в Excel. Вид листа Excel для примера 1 показан в следующей таблице
    A
    B
    C
    D
    E

    1













    2















    3


    2
    -1
    0



    4


    1
    1
    0
    4

    5


    -1
    2
    0
    2

    6


    1
    2
    0
    10

    Данные задачи и формулы в соответствующие ячейки вводятся следующим образом.

    B1:C1 — записаны обозначения переменных модели x1, x2.

    B2:C2 — резервируются для значений переменных модели, которые будут найдены после выполнения процедуры Поиск решения.

    A3:A6 — записаны обозначения строки целевой функции F и строк ограничений b1, b2, b3.

    B3:C3 — записаны коэффициенты при переменных модели в целевой функции.

    B4:C6 — заносим матрицу коэффициентов при переменных в системе ограничений модели.

    Е4:Е6 — записаны правые части системы ограничений модели.

    D3 (целевая ячейка) — вводим формулу: =СУММПРОИЗВ(B3:C3;$B$2: $C$2). «Протягиваем» ее до D6 включительно.

    Запустить команду Поиск решения.

    В диалоговом окне Поиск решения выполнить:

    • установить целевую ячейку равной минимальному значению;

    • изменяя ячейки, ввести адрес переменных;

    • ввести ограничения;

    • выбрать метод решения: Поиск решения задач симплекс-методом.

    Заполненное диалоговое окно Поиск решения имеет вид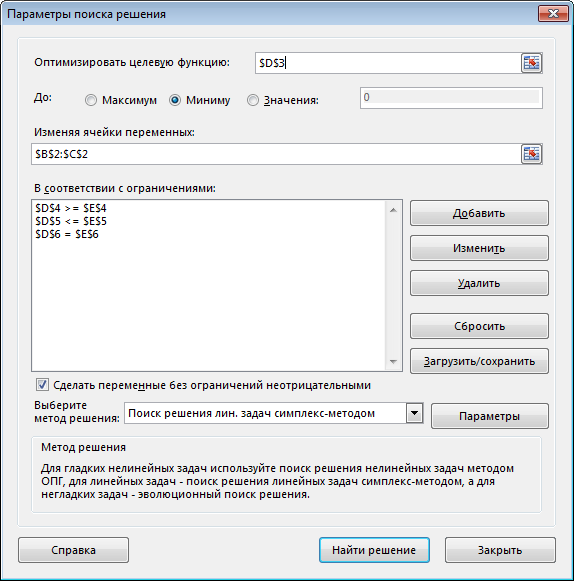



    После выполнения программы работы Поиск решения получим













    4
    3








    2
    -1
    5





    1
    1
    7
    4



    -1
    2
    2
    2



    1
    2
    10
    10

    Оптимальное решение: x = (4; 3). Fmin (x) = 5 ▲

    Пример 2 (задача составления рациона).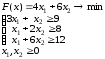



    Анализ данных в Excel. Исходные данные примера 2 на рабочем листе Excel, и заполненное диалоговое окно Поиск решения имеют вид
    A
    B
    C
    D
    E

    1













    2















    3


    4
    6
    0



    4


    3
    1
    0
    9

    5


    1
    2
    0
    8

    6


    1
    6
    0
    12




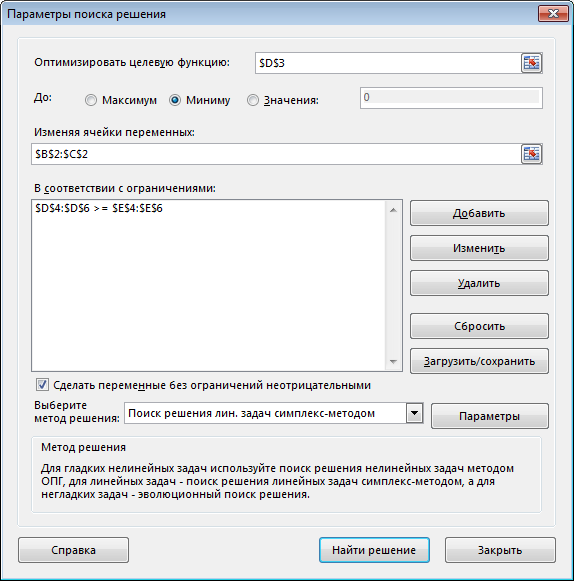    После выполнения программы работы «Поиск решения» получим













    2
    3








    4
    6
    26





    3
    1
    9
    9



    1
    2
    8
    8



    1
    6
    20
    12

    Оптимальное решение: x = (2; 3). Fmin (x) = 26 ▲

    Пример 3 (задача использования ресурсов).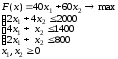



    Анализ данных в Excel. Исходные данные примера 3 на рабочем листе Excel, и заполненное диалоговое окно Поиск решения имеют вид
    A
    B
    C
    D
    E

    1













    2















    3


    40
    60
    0



    4


    2
    4
    0
    2000

    5


    4
    1
    0
    1400

    6


    2
    1
    0
    800



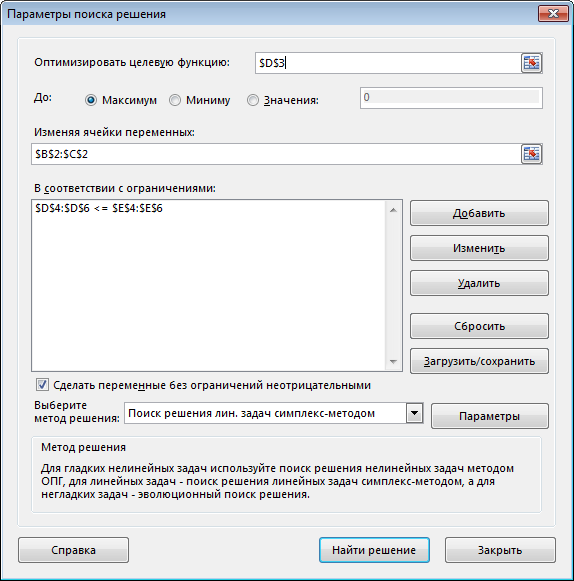    После выполнения программы работы «Поиск решения» получим













    200
    400








    40
    60
    32000





    2
    4
    2000
    2000



    4
    1
    1200
    1400



    2
    1
    800
    800


    Оптимальное решение: x = (200; 400). Fmax (x) = 32000.
    1   2   3   4   5

    написать администратору сайта