ЭММиМ. Задача об использовании ресурсов. Для изготовления двух видов продукции р 1, р 2 используются три вида ресурсов S
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Пример 2. Составить оптимальный план перевозки грузов от трех поставщиков с грузами 240, 40, 110 т к четырем потребителям с запросами 90, 190, 40, 130 т. Стоимости перевозок единицы груза от каждого поставщика к каждому потребителю даны матрицей 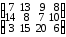 ▼ Рабочий лист Excel и заполненное диалоговое окно Поиск решения имеют следующий вид 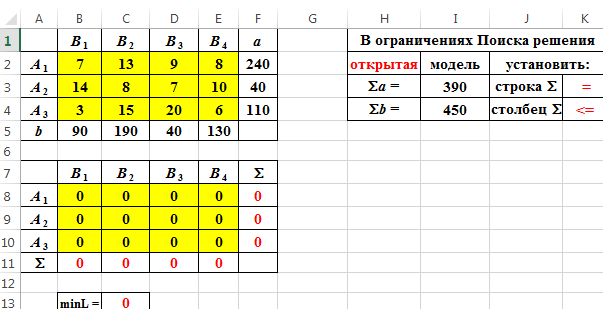 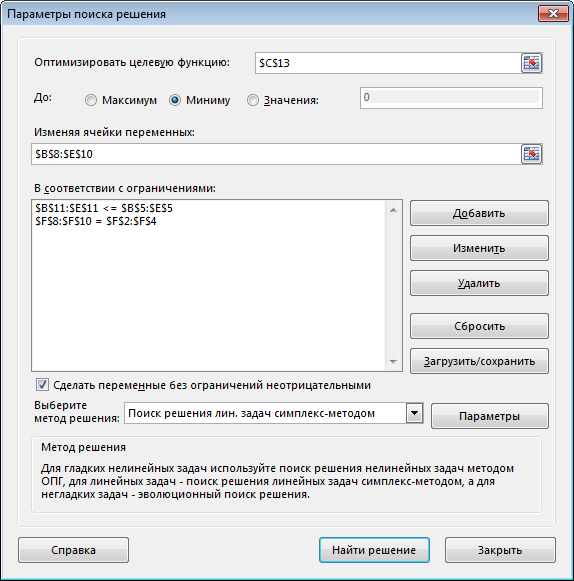 Неравенство $B$11:$E11< = $B$5:$E$5 означает условие неполного удовлетворения потребностей. После выполнения программы работы «Поиск решения» получим
Оптимальное решение  , ,  ▲ ▲Упражнение 1. Три фермерских хозяйства A1, A2, A3 ежедневно могут доставлять в город соответственно 60, 60 и 50 ц молока для обеспечения пяти торговых точек: В1, В2, В3, В4, В5. Стоимость перевозки 1 ц молока и потребности торговых точек в молоке указаны в следующей таблице
Определить оптимальный план поставки молока в каждую точку для удовлетворения потребностей, чтобы суммарные транспортные издержки были минимальными. Ответ: Оптимальное решение 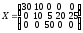 , ,  . .Задачи о назначениях Задача о назначениях имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины и т.п. В наиболее общей форме задача о назначениях формулируется следующим образом. Имеется некоторое число работ и некоторое число работников. Любой работник может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами. Задача о назначениях является частным случаем транспортной задачи, в которой работники соответствуют пунктам отправления, а работы – пунктам назначения. Особенность лишь в том, что все переменные решения принимают только значения 0 или 1 (двоичные переменные) и в каждом столбце и строке может быть только одно ненулевое значение. Точно так же, как и транспортная модель, задача назначений может быть несбалансированной, содержать недопустимые назначения, иметь альтернативные решения при одном и том же значении целевой функции. Эти варианты моделей назначения строятся в полной аналогии с соответствующими транспортными моделями. Для решения задачи о назначениях в Excel с использованием надстройки Поиск решения на рабочем листе следует выделить ячейки назначений и подсчитать для них суммы по столбцам и по строкам. В ячейку целевой функции следует ввести формулу, вычисляющую сумму произведений затрат работ на план назначений. В диалоговом окне Поиск решения выбрать целевую ячейку, изменяемые ячейки и добавить ограничения: суммы значений изменяемых ячеек для каждой строки и столбца должны быть равны 1; переменные должны бть двоичными. Пример 1. Администрация предприятия приняла на работу пять человек. Каждый из них затрачивает различное время на выполнение определенной работы. Необходимо выполнить пять видов работ. Время выполнения работы (с)ij каждым работником приведено в следующей таблице
Требуется назначить на каждый вид работы одного из работников, чтобы общее время, необходимое для завершения всех видов работ, было минимальным. ▼ Экономико-математическая модель задачи Переменные: 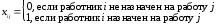 . .Ограничения: по работам: 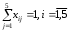 ; ; по работникам:  . .Целевая функция: суммарное время, необходимое для завершения всех видов работ, которое необходимо минимизировать:  Рабочий лист Excel имеет следующий вид 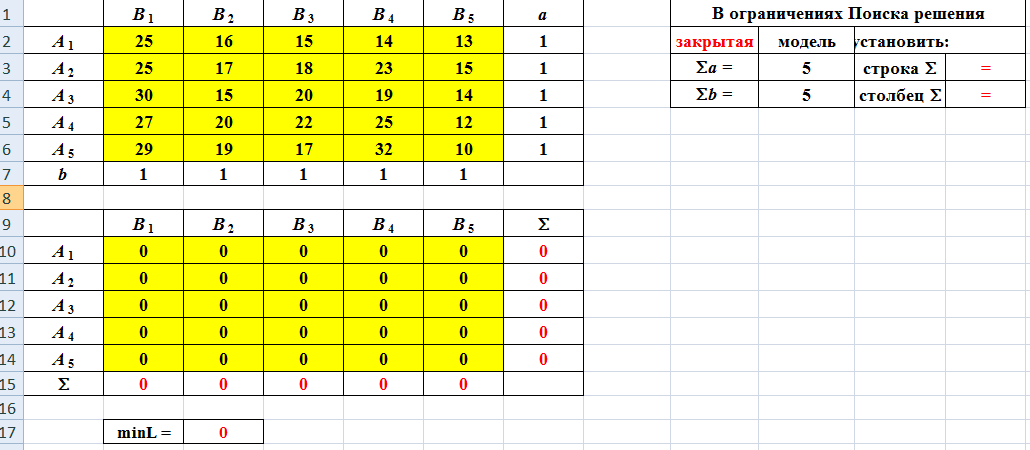 Значения матрицы переменных xij располагаются в ячейках B10:F14. В ячейку С17 введена формула для вычисления значения целевой функции. В ячейках B15:F15 и G10:G14 рассчитываются суммы по строкам и столбцам матрицы переменных. Заполненное диалоговое окно Поиск решения имеют следующий вид 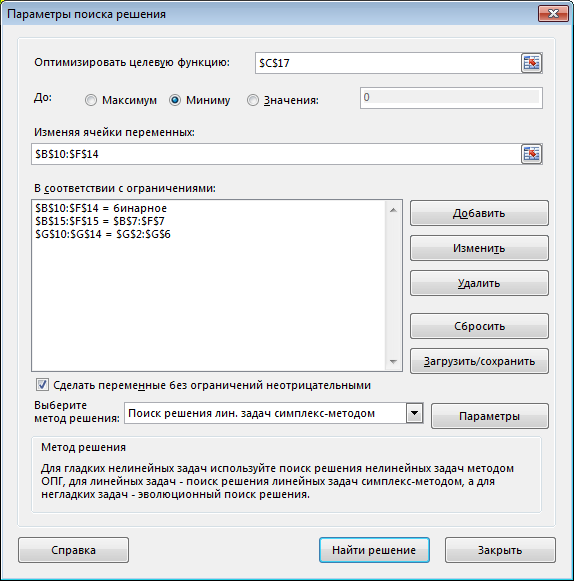 После выполнения программы работы «Поиск решения» получим
Таблица переменных состоит из единиц и нулей. По единицам определяем, что 1- ый работник должен работать на четвертом виде работы, 2- ой на первом, 3- ий на втором, 4- ый на пятом, 5- ый на третьем. Общее время завершения всех видов работ составляет 83 ч. ▲ Пример 2. На предприятии имеется 6 автомобилей разных моделей. Необходимо в разные районы области перевести 5 грузов. Затраты по перевозке каждого груза каждым автомобилем различны и приведены в следующей таблице
Выбрать автомобиль для каждого вида груза так, чтобы затраты на перевозку были минимальными. Определить эти затраты. ▼ В данном примере число автомобилей больше, чем грузов, т.е. один автомобиль окажется невостребованным. Рабочий лист Excel и заполненное диалоговое окно имеют следующий вид  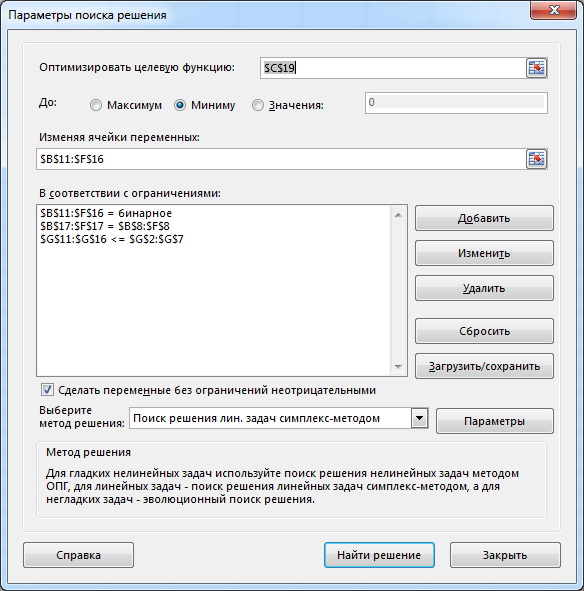 После выполнения программы работы «Поиск решения» получим следующее оптимальное решение
По единицам таблицы определяем закрепление автомобилей за грузами, при этом затраты по перевозке грузов составляют 125 усл. ед. Задача о максимальном потоке Рассмотрим сеть с одним узлом входа (источник) и одним узлом выхода (сток). Для наглядности будем представлять, что по дугам из источника в сток направляется некоторое вещество (количество машин, информации, жидкости и т.п.). Количество вещества, проходящего через дугу в единицу времени, называется потоком по дуге. Предполагается, что поток, вытекающий из узла, равен потоку, втекающему в узел. Величина потока определяется как сумма потоков вдоль дуг, исходящих из источника, или, что то же самое, как сумма потоков вдоль дуг, заходящих в сток. Максимум, или верхнее ограничение на поток в дуге сети будем рассматривать как пропускную способность, или мощность дуги. Мощность потока может зависеть от его направления. Условное изображение в сети 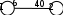 означает, что мощность потока от узла 1 к узлу 2 равна 6, а мощность от 2 к 1 равна 4. Задача о максимальном потоке заключается в нахождении максимальной величины потока, который может войти в систему и выйти из неё в заданный период времени. При этом должны соблюдаться следующие ограничения: поток по каждой дуге не должен превышать ее пропускной способности; общий поток из источника равен общему потоку, приходящему в сток; для промежуточных вершин количество единиц потока, попавшего в данный узел, должно в точности равняться количеству единиц потока, вышедшего из этого узла. величина потока по каждой дуге была целым неотрицательным числом. Задача о максимальном потоке решается как задача линейного программирования. Пример 1. Система автодорог, проходящих через Псковскую область, может обеспечить пропускные способности, показанные на рисунке (тыс. автомашин в час). 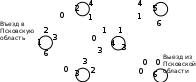 Определим максимальный поток через эту систему. ▼ Расчетные показатели, сформированные на рабочем листе Excel и в режиме просмотра формул показаны на следующих рисунках 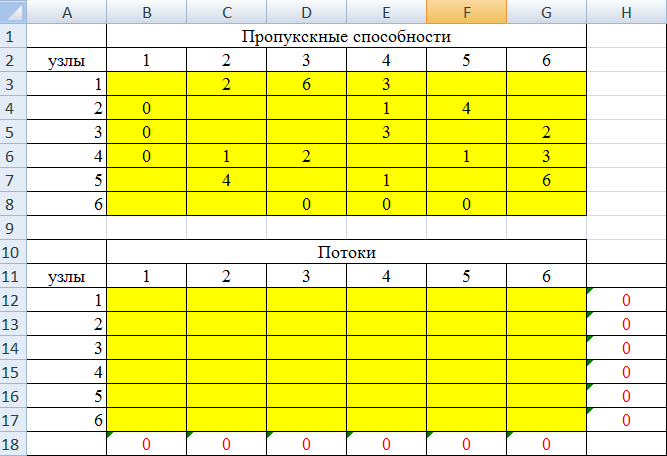 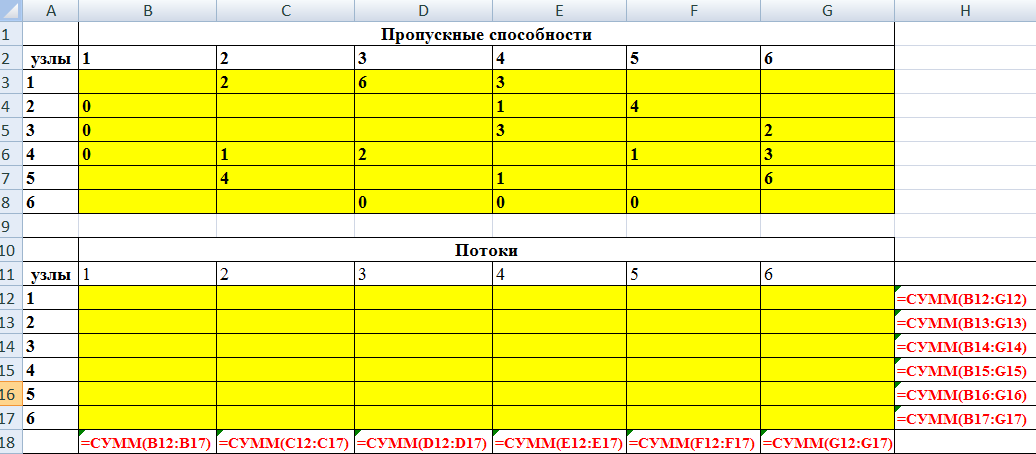 Заполненное диалоговое окно Поиск решения имеет следующий вид 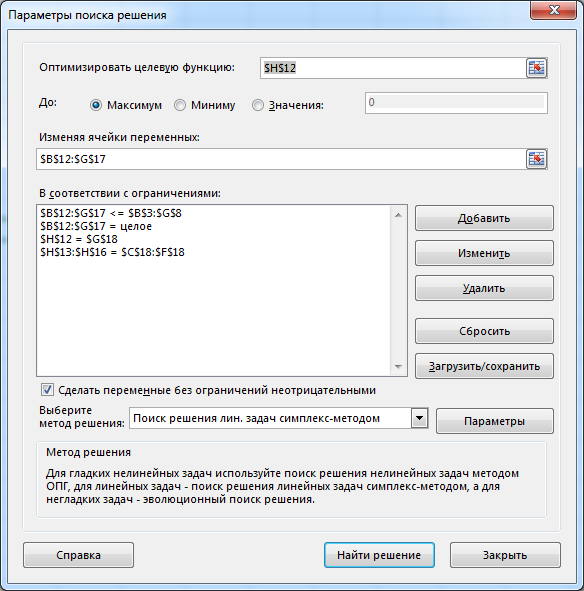 После выполнения программы работы «Поиск решения» получим следующее оптимальное решение: 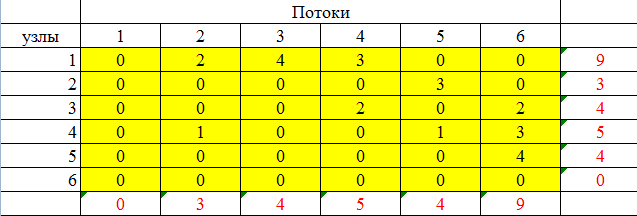 Вывод. Максимальный поток через сеть равен 9 тыс. Конечная модель потоков показана на следующем рисунке. 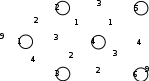 ▲ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
