КР по статистике.. Задача По группе магазинов города имеются следующие данные за отчетный период на основании статистического и финансового учета
 Скачать 38.71 Kb. Скачать 38.71 Kb.
|
|
ВАРИАНТ 3 Задача 3.1. По группе магазинов города имеются следующие данные за отчетный период на основании статистического и финансового учета:
По данным таблицы произвести группировку предприятий по размеру товарооборота, выделив 4 группы (60%). Установить зависимость издержек обращения от товарооборота и среднесписочной численности работников (30%).Сделать выводы (10%). Решение: 1. Группировка: Группировка – это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц совокупности группировка – это объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам. Метод группировки основывается на следующих категориях – это группировочный признак, интервал группировки и число групп. Группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе. Ширина интервала составит: 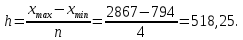 xmax - максимальное значение группировочного признака в совокупности. xmin - минимальное значение группировочного признака. Определим границы группы:
Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп. Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Результаты группировки оформим в виде таблицы:
Задача 3.2. На заводе проведено обследование затрат времени на обработку одной детали. Получены следующие данные:
Исчислите средние и показатели вариации затрат времени на одну деталь: среднюю величину (20%); среднее линейное отклонение (20%); среднее квадратическое отклонение (20%); коэффициент вариации (10%); моду (10%); медиану (10%). Поясните значение каждого показателя (10%). Решение:
1) Для определения средней величины затрат на изготовление одной детали поездок воспользуемся формулой средней арифметической взвешенной: 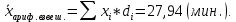 2) Рассчитаем среднее линейное отклонение: 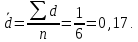 3) Среднее квадратическое отклонение рассчитывается по формуле: 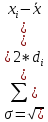 4) Определим коэффициент вариации по следующей формуле: 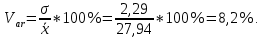 5) Найдем моду и медиану по формулам: 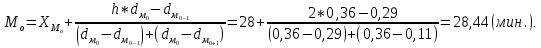 где 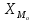 − нижняя граница величины затрат на одну деталь модального интервала; − нижняя граница величины затрат на одну деталь модального интервала;h – шаг интервала, величина интервала; 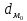 , , 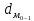 , , 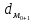 − доля числа рабочих соответственно в модальном, в предшествующем модальному и последующем за модальным интервалах. − доля числа рабочих соответственно в модальном, в предшествующем модальному и последующем за модальным интервалах.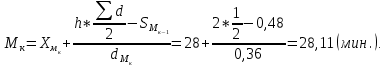 где 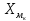 − нижняя граница величины затрат на изготовление одной детали в медианном интервале; − нижняя граница величины затрат на изготовление одной детали в медианном интервале;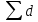 − сумма числа доли рабочих; − сумма числа доли рабочих;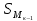 − сумма накопленных частот до медианного интервала; − сумма накопленных частот до медианного интервала;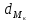 − доля числа рабочих в медианном интервале. − доля числа рабочих в медианном интервале.Вывод: Обследование всего числа рабочих, показало, что средняя величина затрат на изготовление одной детали составляет 27,94 минут. Колебание признака не существенно, а средняя надежна, так как вариация признака составляет 8,2%, что не превышает допустимое значение – 40%. Наиболее часто встречающаяся величина изготовления одной детали – 28,44 минут. Задача 3.3. На предприятии было проведено выборочное обследование возраста рабочих методом случайного бесповоротного отбора. В результате обследования получены следующие данные:
Определить с вероятностью 0.997 пределы, в которых находится средний возраст рабочих предприятия (80%). Можно ли утверждать, что средний возраст работников не превышает 40 лет? Ответ поясните (20%). Решение: Составим таблицу для расчета необходимых данных:
Для начала найдем средний возраст рабочих на предприятии по формуле арифметической взвешенной и дисперсию признака: 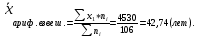 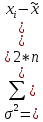 Теперь можно рассчитать среднюю погрешность: 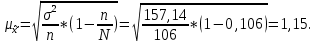 где 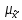 − это средняя погрешность; так как выборка безвозвратная; − это средняя погрешность; так как выборка безвозвратная;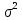 − дисперсия признака; − дисперсия признака;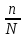 − доля выборки в генеральной совокупности. − доля выборки в генеральной совокупности. Тогда предельная погрешность будет: 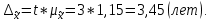 где 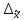 − это предельно допустимая погрешность для выборочной средней; − это предельно допустимая погрешность для выборочной средней;t − это коэффициент доверия Стьюдента, который для вероятности 99,7% имеет значение 3. Средний возраст рабочих на предприятии будет находиться в интервале: 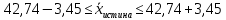 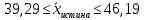 Для того чтоб определить наиболее распространенный возраст необходимо найти моду признака: 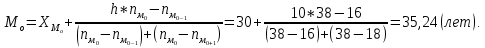 где 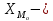 нижняя граница возраста работника модального интервала; нижняя граница возраста работника модального интервала;h – шаг интервала, величина интервала; 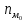 , , 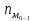 , , 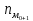 − количество рабочих соответственно в модальном, в предшествующем модальному и последующем за модальным интервалах. − количество рабочих соответственно в модальном, в предшествующем модальному и последующем за модальным интервалах.Вывод: C вероятностью 99,7% можем утверждать, что средний возраст работников на предприятии колеблется от 39,29 до 46,19 лет. Наиболее часто встречающийся возраст среди рабочих 35,24 лет. Задача 3.4. По предприятию имеются следующие данные:
Установить тесноту связи с помощью коэффициента взаимной сопряженности Чупрова (80%). Интерпретируйте значение полученного показателя (20%). Решение: Вычислим коэффициент Чупрова по формуле: 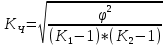 где 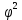 − показатель взаимной сопряженности, − показатель взаимной сопряженности, 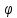 определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. Вычитая из этой суммы 1, получим величину определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. Вычитая из этой суммы 1, получим величину 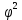 . .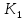 − число значений первого признака, − число значений первого признака,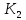 − число значений второго признака. − число значений второго признака.Для начала построим итоговую таблицу, для расчета показателей, которые имеет следующие данные:
Для начала рассчитаем показатель взаимной сопряженности, которая находится по формуле: 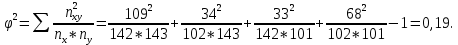 А теперь уже рассчитаем коэффициент Чупрова по формуле: 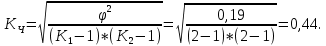 Вывод: Связь умеренная. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
