Задачи mikro. Задача. Расчёт цены земли На четырех одинаковых по площади земельных участках выращивается виноград
 Скачать 161.58 Kb. Скачать 161.58 Kb.
|
1 2 Задача. Расчёт цены земли На четырех одинаковых по площади земельных участках выращивается виноград. Природно-экономические показатели этих земель характеризуют следующие данные:
Определите: цену каждого участка, если известно, что общественная норма прибыли - 15%, а ссудный процент на одолженный у банка капитал равен 5% годовых. Виды ренты способствуют формированию цен на землю? Существует ли дифференциальная рента на I участке? Существует ли дифференциальная рента на II участке? Какие участки обеспечивают этот вид ренты? Назовите причины которые, на ваш взгляд обусловливают разное качество каждого земельного участка? Участки имеют большую производительность? Ответы обоснуйте экономичным анализом. Решение: В основе рыночных цен на сельскохозяйственную продукцию лежит стоимость единицы продукции, полученной с худших земельных участков. Поэтому вся продукция со всех земельных участков будет продаваться по цене, соответствующей стоимости продукции с худшего земельного участка. Худшим земельным участком будет тот, на котором затраты производства 1 т винограда самые высокие. Для простоты анализа составим таблицу расчётных данных:
Продолжение таблицы
Издержки производства включают в данной задаче расходы выращивания и транспортные расходы. Найдём цену земли. Субъект, желающий купить земельный участок, должен учесть альтернативные варианты вложения денег и получения дохода. Субъект выбирает: положить деньги в банк или купить земельный участок. Поэтому при всех неизменных условиях цену земли можно выразить следующей формулой: 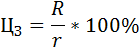 где R – размер арендной платы (рента), r – величина ссудного процента или процентная ставка, Размер арендной платы = Абсолютная рента + Дифференциальная рента + + Процент на капитал Так как в задании не сказано осуществлялись ли ранее капиталовложения в постройки и сооружения, размер арендной платы и размер совокупной ренты будут совпадать. В противном случае арендная плата на ряду с рентой включает в себя выплату процента на вложенный капитал и амортизационные отчисления на вложенный капитал. Таким образом, для нашего задания: Размер арендной платы = Абсолютная рента + Дифференциальная рента = = Совокупная рента Абсолютная рента получается собственниками земли абсолютно со всех земельных участков и абсолютно одинаковой величины, если размеры земельных участков одинаковы. В условии задания сказано, что все четыре участка одинаковы по площади и величина абсолютной ренты равна 300 грн. Дифференциальная рента будет получена собственниками земли только со средних и лучших участков земли, как по качеству и плодородию почвы, так и по месторасположению. Участки, обладающие дифференциальной рентой: I, II и III. IV участок земли будет иметь только абсолютную ренту. Поэтому виды ренты будут способствовать формированию цен на землю. Цена земли IV участка будет зависеть только от величины абсолютной ренты и величины ссудного капитала, в отличии от I, II и III участка, где цена зависит ещё и от величины дифференциальной ренты. Совокупная рента - это избыточная прибыль которую присваивают собственники земли. Можно сказать, что собственник III участка, за счёт наилучшей его производительности получит наибольшую избыточную прибыль. Рассчитаем цены земельных участков. Цена I участка земли: 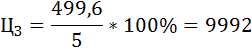 грн. грн.Цена II участка земли: 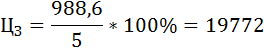 грн. грн.Цена III участка земли: 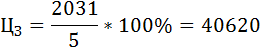 грн. грн.Цена VI участка земли: 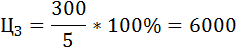 грн. грн.Расчёт общей полезности Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц. Решение: Распишем условие задачи следующим образом: MU(1) = 420, MU(2) = 420/2=210, MU(3) = 210/2=105, MU(4) = 105/4=26,25, MU(5) = 26,25/4=6,5625, MU(6) = 6,5625/4=1,640625, MU(7) = 1,640625/4=0,410156, MU(8) = 0,410156/4=0,102539. Найдём общую полезность блага при условии, что его потребление составляет 8 единиц. TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =...= = MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) = = 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = = 769,96582 Задача № Расчёт оптимального объёма потребления Студент приобретает кофе и пирожки. Цена чашки кофе $2, пирожка $3. При этом он располагает бюджетом в размере $23. Известны предпочтения студента в виде общей полезности:
Как потратить максимум бюджета так, чтобы купить набор этих двух благ с наибольшей полезностью? Сколько она составит? Решение: Оптимальный объём потребления достигается при выполнении второго закона Госсена – закона равной маржинальной (предельной) полезности на единицу затрат: отношение предельной полезности блага к его цене должно быть одинаковым для всех благ. Запишем этот закон в виде тождества: 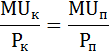 где MUк – предельная полезность кофе, MUп – предельная полезность пирожков, Pк – цена кофе, Pп – цена пирожков. Перепишем это равенство в более удобном виде: 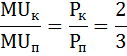 Значит, цены на кофе и пирожки относятся как 2:3. Теперь надо найти такую комбинацию предельных полезностей, чтобы они относились также как 2:3. Рассчёт предельной полезности произведём по формуле: 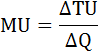 где ΔTU – приращение общей полезности (TU1 – TU0), ΔQ – приращение количества (Q1 – Q0). Так как количество в нашей задаче прирастает каждый раз на единицу ΔQ = 1, можно упростить эту формулу так: MU = ΔTU
В данной задаче три варианта соотношений 2:3 предельных полезностей: 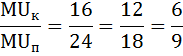 Выпишем эти наборы двух благ: 2 чашки кофе и 4 пирожка, или 4 кофе и 5 пирожков, или 7 кофе и 6 пирожков. Так как бюджет в $23 должен быть израсходован максимально, выберем из этих комбинаций оптимальную. Подставим эти значения в формулу бюджетного ограничения: I = Pк*Qк + Pп*Qп где I – бюджет или доход потребителя, Pк, Pп – цены на кофе и пирожки, Qк, Qп – объём потребления кофе и пирожков соответственно. При Qк = 2, Qп = 4 бюджетное ограничение имеет вид: 23 > 2 × 2 + 3 × 4. В этом случае бюджет израсходован не полностью. При Qк = 4, Qп = 5 бюджетное ограничение имеет вид: 23 = 2*4 + 3*5. Получили верное тождество. Следовательно, оптимальный объем потребления кофе – 4 чашки, а пирожков – 5 штук. При этом бюджет истрачен полностью. Общая полезность составит: TU = 62 + 135 = 197. Задача Расчёт параметров равновесия на рынке монополистической конкуренции Известно, что в долгосрочном периоде средние переменные затраты монополистически конкурентной фирмы зависят от объема производства АVС = Q + 10. Спрос на продукцию фирмы описывается формулой Р = 150 – 3Q. Найдите параметры равновесия (цену и объем продаж) и сделайте вывод, находится фирма в состоянии долгосрочного или краткосрочного равновесия. Нарисуйте график. Решение: Найдём функцию переменных затрат: VC = АVС × Q = (Q + 10) × Q = Q2 + 10 × Q В долгосрочном периоде постоянные затраты равны нулю, следовательно, функция общих затрат будет иметь вид: ТС = VC + FC = Q2 + 10 × Q Соответственно функция средних общих затрат будет равна функции средних переменных затрат: ATC = АVС = Q + 10 Предельные затраты фирмы на рынке определим как производную от функции общих затрат: 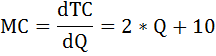 Выручка фирмы на рынке будет равна: TR = P × Q = (150 – 3 × Q) × Q = 150 × Q – 3 × Q2 Найдём предельную выручку как производную от общей выручки: 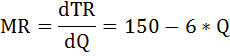 При равновесии в долгосрочном периоде в условиях монополистической конкуренции выполняются равенства: P = ATC, MC = MR. Приравняем функцию предельных затрат к функции предельной выручки: 2Q + 10 = 150 – 6Q Отсюда оптимальный объём выпуска фирмы равен: Q = 17,5 Подставим это значение в равенство цены и средних общих издержек: 150 – 3 × 17,5 = 17,5 + 10 97,5 ≠ 27,5 P ≠ ATC Следовательно, одно из условий равновесия долгосрочного периода не соблюдается, что свидетельствует о состоянии краткосрочного равновесия. 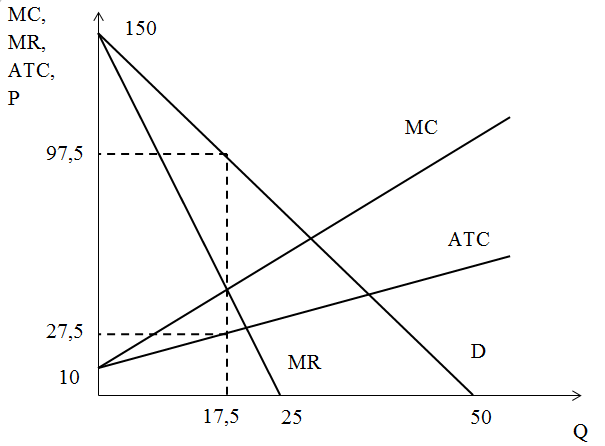 Задача Расчёт цены монополиста Монополия на рынке имеет следующую функцию предельных издержек: МС = - 10 + 3 × Q. Предельный доход выражен функцией: MR = 40 - 2 × Q. Какова цена, назначаемая монополией за свой продукт на рынке? Решение: Известно, что предельный доход определяется дифференцированием функции общего дохода. Найдём функцию общего дохода, то есть первообразную от функции предельного дохода: 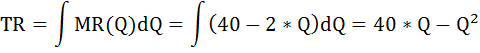 Из формулы общего дохода выразим цену: TR = P × Q ⇒ P = TR / Q = (40 × Q - Q2) / Q = 40 - Q Получили обратную функцию спроса: P = 40 - Q. Теперь из условия максимизации прибыли найдём оптимальный объём производства монополии. MC = MR - 10 + 3 × Q = 40 - 2 × Q Q = 10 Подставим это значение в функцию спроса и рассчитаем цену, назначаемую монополией за свой продукт на рынке: Р = 40 - 10 = 30. Задача Расчёт изменения объёма выпуска фирмы Средние издержки конкурентной фирмы описываются формулой: АС = 40 + 2Q Как изменится объём выпуска фирмы, если цена на продукцию с 200 руб. за штуку упадёт до 100 руб. за штуку? Решение: В условиях совершенной конкуренции фирма получает максимальную прибыль, если выполняется равенство: МС = Р Для определения предельных издержек необходимо знать либо функцию общих издержек ТС, либо функцию переменных издержек VC. Найдём функцию общих издержек. Так как АС = ТС / Q, отсюда ТС = AC × Q. ТС = 40Q + 2Q2 Теперь можно найти функцию предельных затрат по формуле: МС = ТС' = (40Q + 2Q2)' = 40 + 4Q Первоначально цена была равна 200 руб. Значит, объём выпуска, который выберет фирма, максимизирующая прибыль, будет равен 40: МС = Р1 40 + 4Q1 = 200 Q1 = 40 Затем цена упала до 100 руб. за штуку. Объём выпуска стал равным 15: МС = Р2 40 + 4Q2 = 100 Q2 = 15 Изменение объёма выпуска составит: ΔQ = Q2 - Q1 = 40 - 15 = 25 Определение точки закрытия фирмы Определить точку закрытия фирмы, если известно, что функция её общих затрат имеет вид: ТС = 40 + 2Q - 0,5Q2 + 0,25Q3. Решение: Точка закрытия конкурентной фирмы - минимальная точка на кривой средних переменных издержек; фирма прекратит свою производственную деятельность и покинет рынок, если цена упадёт ниже этой точки. Задача сводится к нахождению минимума функции средних переменных издержек. Функция переменных издержек будет равна: VC = 2Q - 0,5Q2 + 0,25Q3 (Как определить функцию переменных издержек можно посмотреть здесь) Средние переменные издержки найдём по формуле: AVC = VC / Q = 2 - 0,5Q + 0,25Q2 Далее приравняем к нулю производную этой функции и найдём значение выпуска, при котором средние переменные затраты минимальны. - 0,5 + 0,5Q = 0 0,5Q =0,5 Q = 1 Рассчитаем минимум средних переменных затрат: AVC (1) = 2 - 0,5*1 + 0,25*12 = 1,75 Следовательно, при цене ниже 1,75 и объёме производства равном 1 фирма закроется. Задача Расчёт цены и объёма производства, максимизирующих прибыль Спрос на продукцию конкурентной отрасли: Qd = 55 – P Предложение: Qs = 2P – 5 Если у одной из фирм отрасли восходящий участок кривой предельных издержек: МС = 3Q + 5 При каких цене и объёме производства фирма максимизирует прибыль? Решение: Найдём цену равновесия. Приравняем функцию спроса и предложения: Qd = Qs 55 – P = 2P – 5 3 * Р = 60 Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию. Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат. МС = Р 3Q + 5 = 20 Q = 5 – объём производства, при котором прибыль фирмы будет максимальной. Задача Определение функций постоянных, переменных, предельных и средних издержек Функция общих издержек имеет вид: TC = 3Q2 + 5Q + 20 Определить функции: а) постоянных и переменных издержек; б) средних постоянных, переменных и общих (совокупных) издержек; в) предельных издержек; Решение: а) Общие издержки TC состоят из постоянных FC, которые не зависят от объёма выпускаемой продукции, и переменных издержек VC, которые связаны с объёмом производства Q. Рассмотрим функцию общих издержек: TC = 3Q2 + 5Q + 20 В этой функции, слагаемые содержащие переменную Q и есть переменные издержки, то есть функция переменных издержек имеет вид: VC = 3Q2 + 5Q , а постоянные издержки соответственно равны: FC = 20. б) Функция средних постоянных издержек AFC будет равна отношению постоянных издержек FC к объёму выпущенной продукции Q: 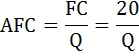 Функция средних переменных издержек AVC будет равна отношению переменных издержек VC к объёму выпущенной продукции Q: 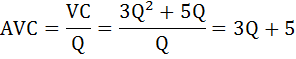 Функция средних общих издержек ATC (или АС) будет равна отношению общих издержек TC к объёму выпущенной продукции Q: 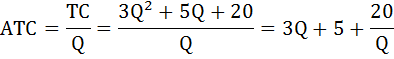 в) Функция предельных издержек MC получается путём дифференцирования функции совокупных издержек: Не трудно заметить, что тот же результат получится, если вместо функции общих издержек TC взять функцию переменных затрат VC: Задача Расчёт максимума прибыли монополиста Найти максимум прибыли монополиста, если известно, что спрос на его продукцию описывается функцией: Q = 165 - 0,5 × P и функция общих затрат равна: TC = 5500 + 30 × Q + Q2 Решение: Условие максимизации прибыли на монопольном рынке состоит в равенстве предельных издержек и предельного дохода: MC = MR Предельные издержки определим по формуле: МС = TC' =(5500 + 30 × Q + Q2)' = 30 + 2Q Найдём обратную функцию спроса: Q = 165 - 0,5 × P ⇒ P = 330 - 2 × Q Функция общего дохода будет иметь вид: TR = P × Q = (330 - 2Q)Q = 330Q - 2Q2 Предельный доход рассчитаем по формуле: MR = TR' = (330Q - 2Q2)' = 330 - 4Q 30 + 2Q = 330 - 4Q 6Q = 300 Q = 50 - оптимальный выпуск фирмы. Цена продукции этом будет равна: P = 330 - 2 × 50 = 230. Рассчитаем прибыль монополиста по формуле: П = TR - TC = Р × Q - (5500 + 30Q + Q2) П = 230 × 50 - 5500 - 30 × 50 - 502= 2000. Задача Расчёт дисконтированного дохода Если бы вам предложили на выбор два варианта: а) получать 2600 ден. ед. каждый год до самой смерти; б) получить 5000 ден. ед. через год, 8000 – в конце второго года и 20600 – в конце третьего года. Ставка процента 10 %. Какой из вариантов Вы предпочтете? Решение: Поскольку число жизни не известно, то при ставке 10% по варианту а) дисконтированный доход составит не более 26000 ден. ед.: 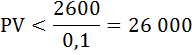 По варианту б) дисконтированный доход составит: 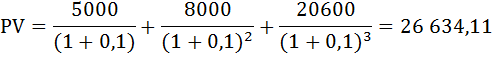 Задача Купить или арендовать? Арендная плата за дом составляет 15000 $ в год, этот же дом можно купить за 180000 $. Процентная ставка по депозитам находится на уровне 10% годовых. Что выгоднее: аренда или покупка дома? Решение: Выгоднее аренда. В случае аренды дома в течение всей жизни (пока арендуется дом) придётся выплачивать арендную плату, дисконтированная ценность которой составит 150 000 (15 000/0,1). А так как 150 000 < 180 000, то выгодно снимать дом в аренду, нежели его покупать. № Расчёт уровня занятости монополиса-монопсониста Фирма является монопсонией на рынке труда и монополией на товарном рынке. Заполните таблицу спроса на труд этой фирмы. Определите, сколько рабочих наймёт эта фирма, и какую установит ставку заработной платы.
Решение: Валовой доход рассчитывается как произведение цены на продукт труда: TR = P × Q P - цена, Q - совокупный продукт. Если фирма располагает одной единицей труда, её валовой доход будет равен: TR = 40 × 5 = 200 Доход от предельного продукта - предельная выручка от предельного продукта (MRPL) - определяется произведением предельной выручки MR и предельного продукта труда MP: 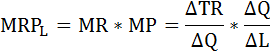 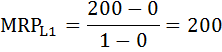 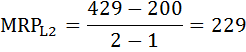 и т. д. и т. д.Предельные затраты на оплату труда определяются по формуле: 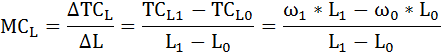 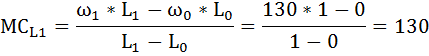 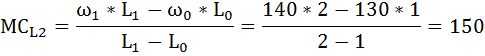 и т. д. и т. д.Рассчитаем также ценность предельного продукта труда VMPL по формуле: VMPL = MP × Р и добавим ещё одну графу в таблице.
Фирма является монопсонией на рынке труда и монополией на товарном рынке. Оптимум такого предприятия, как показано на рисунке, определяется пересечением кривых предельных затрат на труд MCL и предельной выручки, приносимой данным фактором MRPL. 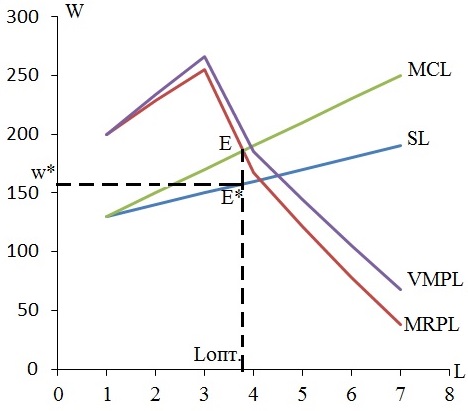 Пока предельная выручка от предельного продукта превышает предельные затраты на оплату труда MRPL > MCL, фирма продолжает нанимать сотрудников до точки оптимума Е, чтобы достичь прибылемаксимизирующего уровня занятости. Увеличение занятости до Lопт. увеличивает прибыль фирмы, тогда как дальнейшее увеличение сопровождается её снижением. При этом ставка заработной платы, которую будет выплачивать монопсонист-монополист нанятым работникам w*, будет соответствовать точке E*. Следовательно, наняв трёх работников фирме следует прекратить найм, так как дополнительно нанятый работник повлечёт снижение прибыли, так как при этом MRPL < MCL. Для L = 3 ставка заработной платы w = 150. Задача. Расчёт оптимального выпуска продукции Фирма находится в условиях совершенной конкуренции на рынке данного товара и труда. Ее производственная функция имеет вид Q = 120 × L – 2 × L 2 в интервале использования труда от 12 до 30 единиц. Ставка заработной платы равна 60 ден. ед., а цена товара 8 ден. ед. Определить оптимальный для фирмы выпуск продукции. Решение: Общее условие максимизации прибыли при покупке фактора производства. Для того чтобы получить максимальную прибыль произведя и продав продукцию на рынке готовой продукции фирма на рынке труда должна нанять такое количество работников, чтобы выполнялось следующее: MRPL = MIC где MRPL – предельная доходность труда, МIC – предельные издержки на фактор производства (труд). MRPL = MR × MPL где MR – предельная выручка, MPL – предельный продукт труда. Фирма находится в условиях совершенной конкуренции на рынке данного товара и на рынке труда. Фирма, продающая продукцию на совершенно конкурентном рынке, не может повлиять на рыночную цену, она принимает её как заданную и в этом случае: Р = МR На рынке труда издержки фирмы на труд равны ставке заработной платы: MIC = ω, где ω – ставка заработной платы Таким образом, для совершенно конкурентной во всех отношениях фирмы условие максимизации прибыли при покупке фактора производства будет иметь вид: P × MPL = ω Продифференцируем производственную функцию и найдём предельный продукт труда (MPL) по формуле: 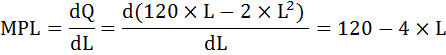 Подставим это выражение в условие максимизации прибыли и найдём количество нанимаемого труда: 8 × (120 – 4 × L) = 60 960 – 32 × L = 60 900 = 32 × L L = 28,125 Оптимальный для фирмы выпуск продукции будет равен: Q = 120 × 28,125 – 2 × 28,125 2 = 1793 Задача Фирма, действующая на рынке совершенной конкуренции, сделала все необходимое для максимизации своей прибыли, но, тем не менее, получила убыток в среднем в размере 14 р. с каждой проданной единицы продукции. Общая выручка фирмы составила 660 р., а предельная выручка от продажи последней единицы оказалась равной 12 р. Определите величину общих издержек фирмы (ТС). 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
