Задачи mikro. Задача. Расчёт цены земли На четырех одинаковых по площади земельных участках выращивается виноград
 Скачать 161.58 Kb. Скачать 161.58 Kb.
|
1 2 Решение:Фирма, действующая на рынке совершенной конкуренции, максимизирует свою прибыль, если выполняется равенство: P = MC = MR = AR. По условию предельная выручка MR от продажи последней единицы равна 12. Впрочем, как и от продажи любой другой единицы на рынке совершенной конкуренции. Следовательно, и цена на рынке будет равна 12. MR = P = 12 Зная величину общей выручки и цены, найдём объём производства: Q = TR / P = 660 / 12 = 55 Прибыль фирмы определяется по формуле: П = TR – TC = P × Q – AC × Q = Q × (P – AC) По условию задачи фирма получила убыток с каждой проданной единицы продукции в размере 14 р.: 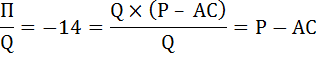 Так как Р – АС = –14 и Р = 12, отсюда АС = 26. Итак, средние издержки при оптимальном объёме выпуска равном 55 равны 26. Найдём общие издержки при оптимальном объёме, используя формулу средних затрат: 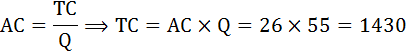 Определение рыночной цены и отраслевого выпуска продукции В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями ТС =Q3 - 36*Q2 + 384*Q, где Q - объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие. Решение: В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство: P = MC = MR = AR = minAC. Найдём функцию средних издержек каждой фирмы по следующей формуле: АС = ТС / Q = Q2 - 36*Q + 384 Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю. 2*Q - 36 = 0 Q = 18 AC(18) = 182 - 36*18 + 384 = 60 Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60. Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут: Qотр. = 18*130 = 2340 тысяч штук Задача. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют: Q3 – 16*Q2 + 400*Q. а) При каком значении Q средние затраты достигают минимума? б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде? Решение: а) Найдём функцию средних затрат по формуле: АС = ТС / Q = (Q3 – 16*Q2 + 400*Q) / Q = Q2 – 16*Q + 400 Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю. AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16 2*Q – 16 = 0 Q = 8 При Q = 8 средние затраты достигают минимума. б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие: Р = МС = MR = minАС Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат: minAC(Q=8) = 82 – 16*8 + 400 = 336 Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде. Расчёт рыночной цены и объёма выпуска на конкурентном рынке Конкурентная фирма имеет общие затраты ТС = 800 + 40*Q + 2*Q2 Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000. Определить цену на рынке и объём выпуска данной фирмы. Решение: Формула прибыли фирмы имеет вид: П = TR - TC = P*Q - TC По условию максимально возможная прибыль равна 1000. P*Q - (800 + 40*Q + 2*Q2) = 1000 Найдём цену. Условие максимизации прибыли на рынке совершенной конкуренции имеет вид: Р = МС = MR = AR Так как Р = МС, а МС = ТС' = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим: (40 + 4*Q)*Q - (800 + 40*Q + 2*Q2) = 1000 40*Q + 4*Q2 - 800 - 40*Q - 2*Q2 - 1000 = 0 2*Q2 = 1800 Q2 = 900 Q1,2 = ±30 Так как отрицательный корень экономического содержания не имеет, берём Q = 30. Тогда цена будет равна: Р = 40 + 4*30 = 160 Выбор оптимального объёма производства Зависимость общих затрат предприятия (ТС) от выпуска представлена в таблице:
На рынке цена установилась на уровне 110 р. а) Сколько продукции должно производить предприятие, чтобы достичь максимума прибыли? б) Не следует ли прекратить производство? в) Ниже какого уровня должна снизиться цена, чтобы предприятие прекратило производство данного товара? Решение: а) Прибыль достигает максимума, когда MR = MC, в точке, в которой кривая предельных издержек возрастает, а не снижается. Так как цена не зависит от объёма продаж и равна 110 рублей, следовательно, данное предприятие работает в условиях совершенной конкуренции. Кроме этого, так как при Q = 0 фирма несёт издержки (постоянные затраты, независящие от объёма выпуска FC = 100 р.), речь идёт о краткосрочном периоде. На конкурентном рынке предельный доход и цена равны: MR = P. Условие максимизации прибыли для конкурентной фирмы заключается в выборе такого объёма выпуска продукции, чтобы цена равнялась предельным издержкам: Р = МС. Найдём предельные издержки этого предприятия по формуле: МС = ΔТС / ΔQ
Как видно из таблицы равенство Р = МС не соблюдается ни при каком объёме выпуска. При Q = 3, Р > МС, а при Q = 4, Р < МС. Выпустив три единицы продукции, предприятию следует остановиться, так как прирост выпуска на единицу скорее снизит, а не увеличит прибыль, то есть добавление четвёртой единицы продукции приносит убыток. б) Существует единый критерий для любого временного периода: фирма продолжает работу в отрасли, если при достижении максимума прибыли (отличного от П(0)) её выручка больше или равна значению переменных издержек. Выручка при Q = 3 равна TR = PQ = 110*3 = 330 р. Переменные издержки равны разности общих и постоянных затрат: VC = TC - FC = 300 - 100 = 200 р. Так как выручка больше переменных издержек TR > VC, фирма продолжает работу. Производство прекращать не следует. в) Для того, чтобы предприятие прекратило производство данного товара нужно, чтобы цена опустилась ниже минимума средних переменных затрат: Р < min AVC. Рассчитаем средние переменные издержки как отношение переменных затрат к объёму выпуска: 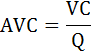 Переменные затраты определим как разность общих и постоянных затрат. Результаты занесём в таблицу.
Минимум средних переменных затрат равен 40 р. Значит, чтобы предприятие прекратило производство данного товара нужно, чтобы цена опустилась ниже 40 р. 1 2 |
