эконометрика. ммм вар 22. Задача состоит в нахождении такой допустимой производственной программы
 Скачать 184 Kb.
|
Содержание 1. Ситуационная (практическая) часть………………………………………………..3 2. Тестовая часть………………………………………………………………………..8 Список литературы……………………………………………………………………10 1. Ситуационная (практическая) часть Предоставить подробное решение задачи 1 и задачи 2 с необходимыми чертежами. Задача 1. 1. Построить математическую модель оптимизации выпуска продукции и записать ее в форме задачи линейного программированияВведем перемнные: Пусть х1 – месячный объем выпуска продукции А; х2 – месячный объем выпуска продукции В. Используя данные таблицы, определим затраты каждого вида ресурса для выпуска производственной программы Х*=(х1, х2): Расход сырья: 4х1+х2 102; Загрузка оборудования: х1+2х2 223; Трудозатраты: 8х1+х2 142; Задача состоит в нахождении такой допустимой производственной программы Х=(х1, х2), которая обеспечивает получение наибольшего дохода: Z=440х1+63х2 max; Построенная математическая модель задачи представляет собой задачу линейного программирования, так как ограничения заданы в виде линейных неравенств, а оптимизируемый показатель (доход) выражается с помощью линейной функции. Таким образом, математическая модель данной задачи выглядит следующим образом: 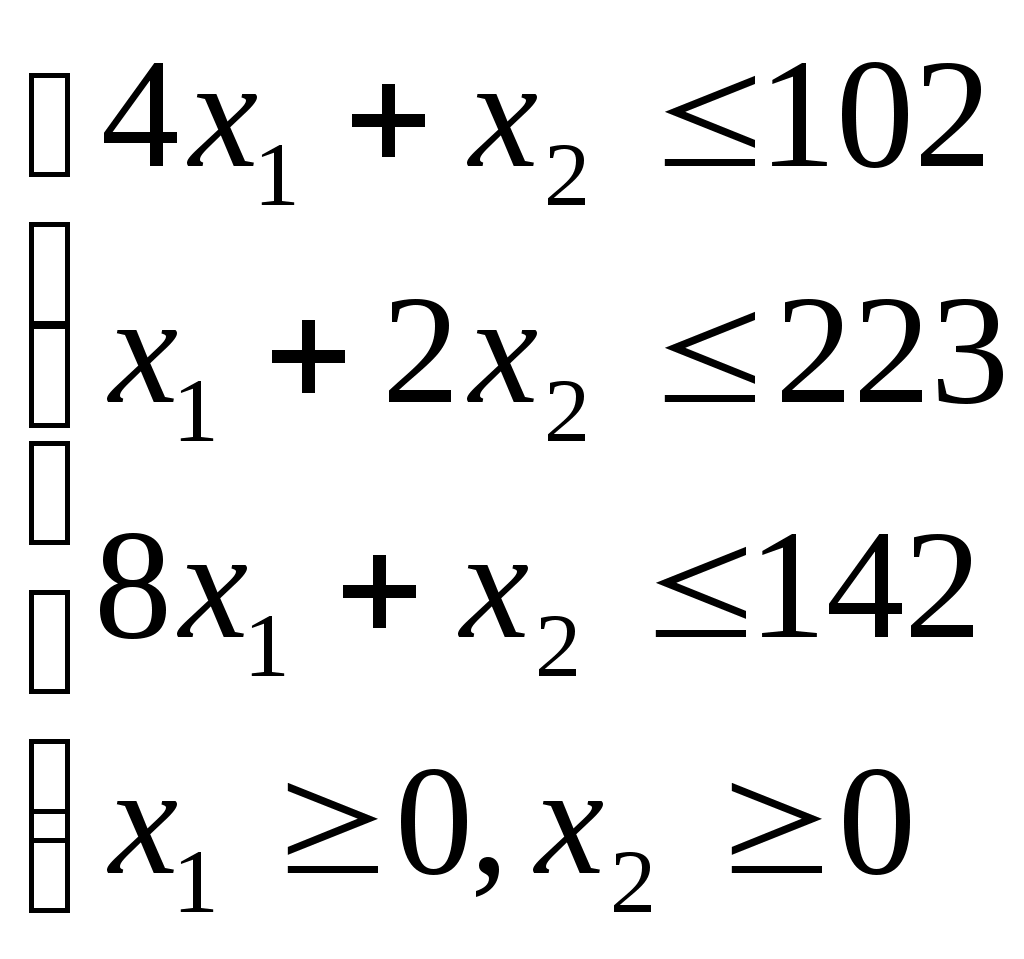 Целевая функция прибыли: Z=440х1+63x2 max 2. Используя графический метод решения задачи линейного программирования, найти оптимальную программу выпуска продукции. Первым шагом в графическом методе решения является построение множества допустимых решений (МДР), для ее построения необходимо построить граничные прямые, уравнения которых получаются из неравенств при замене знака «» на «=». 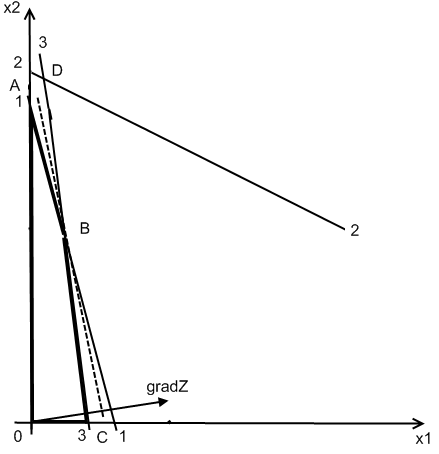 рис. 1. На рис. 1. показано МДР. МДР представляет собой многоугольник OABC. Для нахождения точки максимума целевой функции Z=440х1+63х2 нужно построить градиент функции Z, он равен: 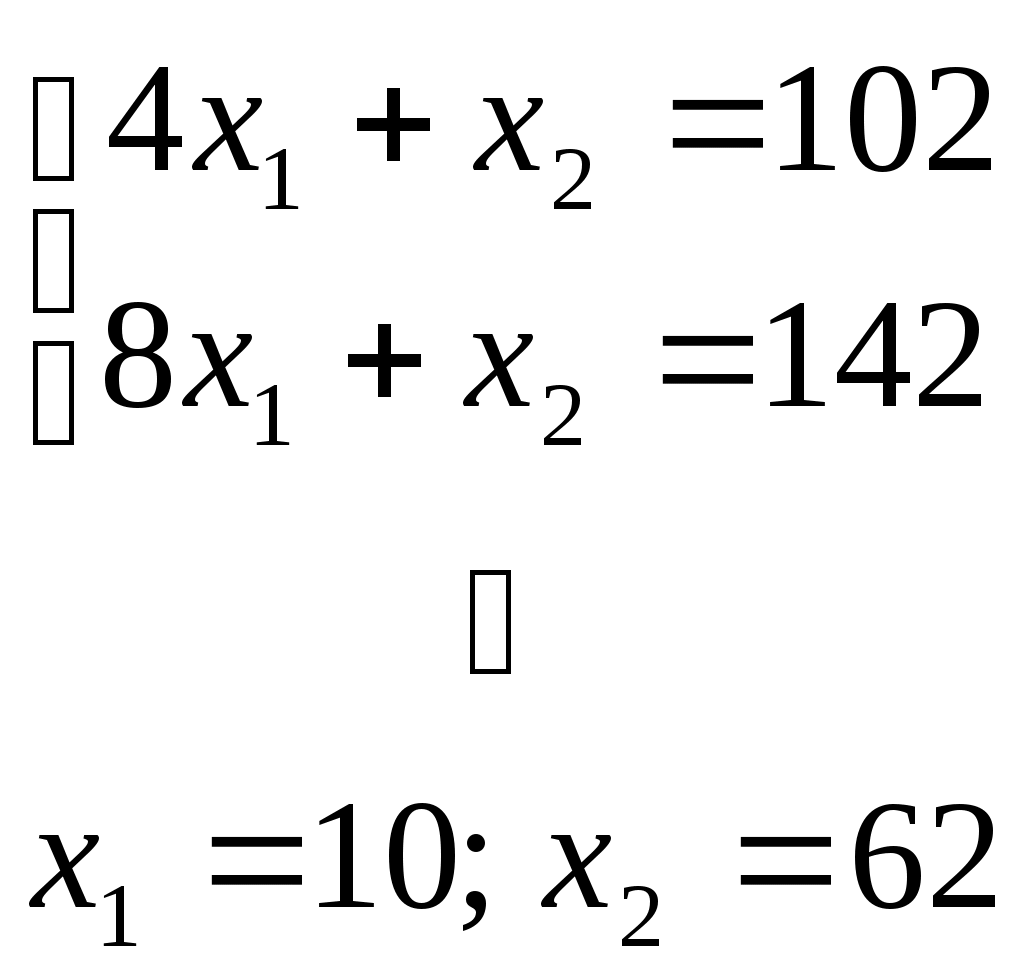 . Из начала координат в направлении к точке (44;6,3) проводим вектор. Перпендикулярно вектору проводим некоторую прямую, которая будет являться линией уровня линейной функции Z. Двигая линию уровня параллельной самой себе в направлении grad Z, можно найти точку максимума, ей будет являться точка Х* - самая последняя точка МДР, с которой пересечется линия уровня. В нашей задаче точкой максимума является точка В, которая лежит на пересечении линий (1) и (3). Её координаты можно найти, решив систему уравнений: Тогда максимальный доход от реализации изделий А и В составит:  (руб.)Оптимальная производственная программа состоит в выпуске 10 изделий вида А и 62 изделий вида В. 3. Составив задачу, двойственную к задаче оптимизации выпуска продукции, найти ее оптимальное решение, используя условия «дополняющей нежесткости». Дать экономическую интерпретацию этого решения. Каждому ресурсному ограничению исходной задачи сопоставляется двойственная переменная (оценка). Так как в нашей задаче рассматриваются три ресурса, то введем для них три оценки, которые обозначим через u1, u2, u3: 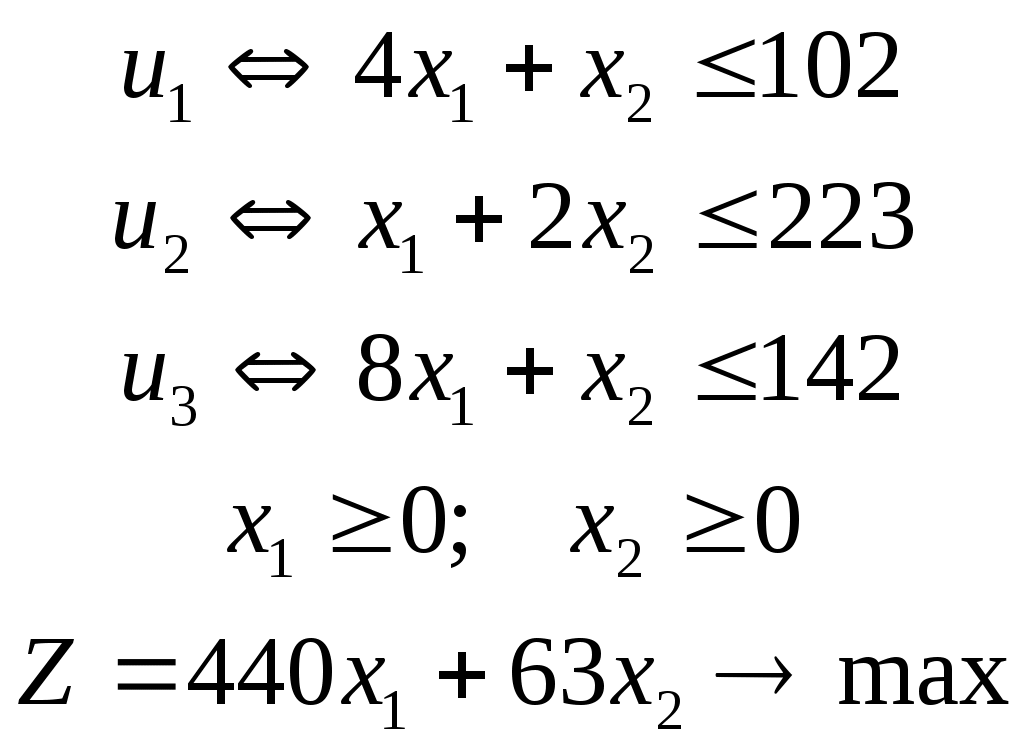 Тогда двойственная задача будет иметь вид: 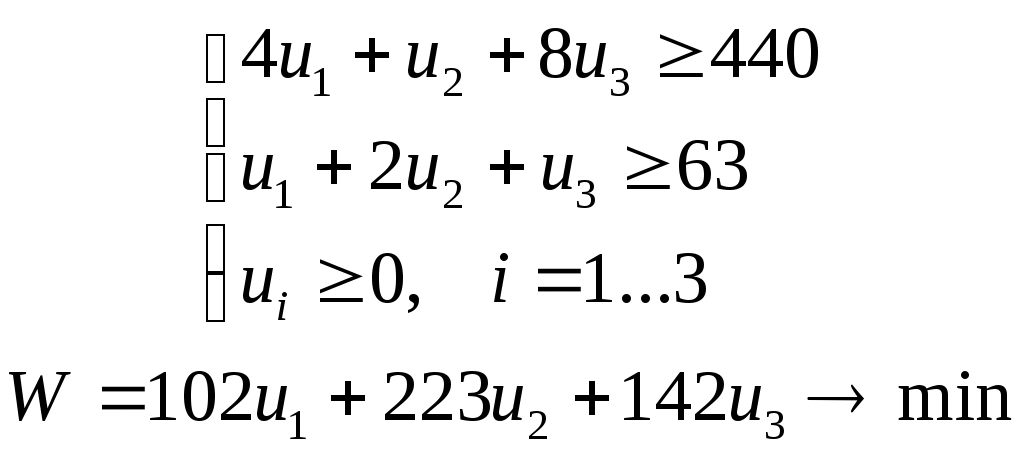 Допустимые решения 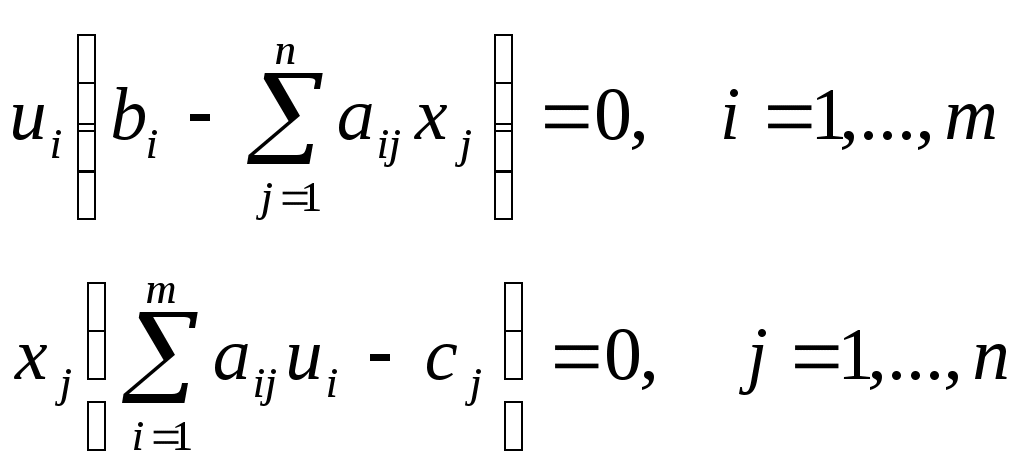 прямой и двойственной задачи оптимальны тогда и только тогда, когда выполняются условия «дополняющей нежесткости»: Для рассматриваемой задачи имеем: 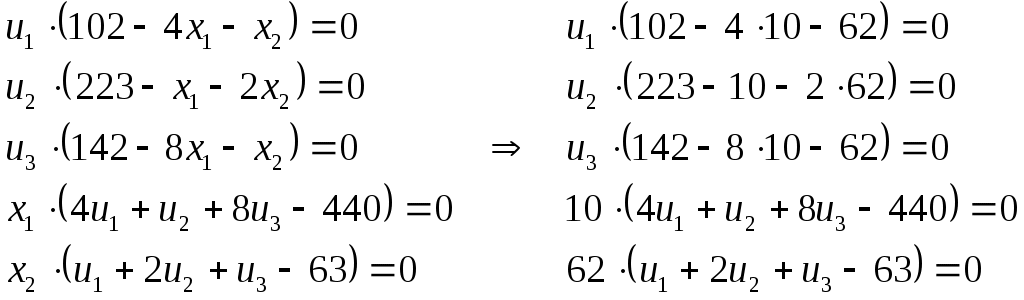 Таким образом, получаем: 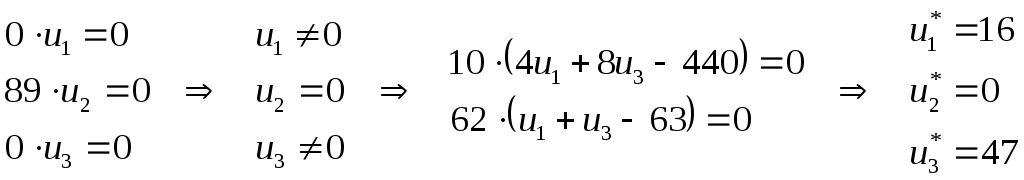 Тогда значение целевой функции двойственной задачи составит:  (руб.), таким образом, значения целевых функций исходной и двойственной задач совпадают.В итоге получили следующие результаты расчета модели: Х*=(10;62); U*=(16;0;47); Z*=W*=8306 Оптимальные двойственные оценки имеют четкую экономическую интерпретацию. Они являются количественной мерой предельной полезности или эффективности использования ресурсов. Оптимальная оценка ресурса характеризует абсолютное увеличение оптимизируемого показателя Z в случае увеличения (снижения) объема этого ресурса на одну единицу. Стоимостная оценка сырья  руб./кг. означает, что при увеличении количества используемого в производстве сырья с 222 кг. до  кг., увеличение максимальной суммарной выручки составит  руб., а при уменьшении сырья на  выручка уменьшится на  руб.Стоимостная оценка времени работы оборудования  означает, что ни увеличение, ни уменьшение времени работы оборудования в производстве продукции не приведет к изменению оптимального значения суммарной выручки. Действительно, количество времени работы оборудования для производства оптимальных объемов продукции  составит  ст.час, а предприятие располагает 223 ст.час. трудовых ресурсов. Следовательно,  ст.час. времени работы оборудования остаются неиспользованными. Поэтому увеличение или сокращение используемого времени работы оборудования (но не более, чем на 89 ст.час), не приведет к изменению оптимального значения суммарной выручки.Стоимостная оценка трудовых ресурсов  руб./ст.-час. означает, что при увеличении месячного фонда трудовых ресурсов с 142 чел.-час. до  чел.-час. увеличение максимальной суммарной выручки составит  руб., а при уменьшении фонда времени на выручка уменьшится на  руб.Задача 2 Применяя данные таблицы задачи 1, построить график функции предельной полезности сырья для данного предприятия. В задаче оптимизации выпуска продукции оптимальное решение достигается в точке В, являющейся точкой пересечения прямых (1) и (3). Найдем интервал устойчивости изменения сырья.(см. рис.1.) Количество используемого сырья, соответствующего точке D (4,1 ; 109,5):  кгКоличество используемого сырья, соответствующего точке С (17,75 ; 0):  При изменении объема используемого сырья от 71 до 125,9 кг точка B оптимального решения будет перемещаться в пределах отрезка СD и будет соответствовать точке пересечения линий (1) и (3). Координаты этой точки можно найти из системы уравнений: 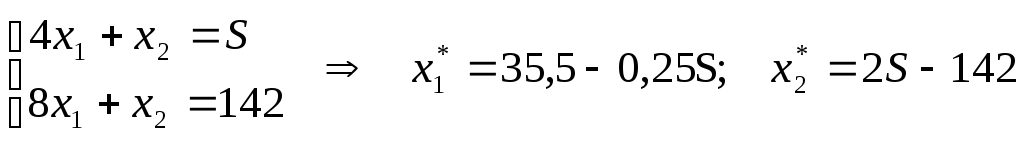 Используя условие дополняющей нежесткости, имеем: 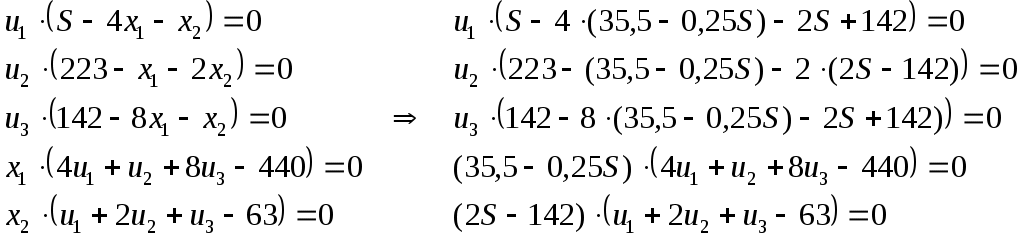 Таким образом, получаем (имея в виду, что 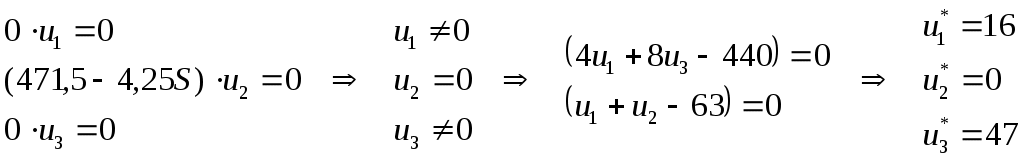 ): Тогда  Очевидно, что дальнейшее увеличение сырья не окажет никакого влияния на изменение оптимального решения, т.е. при  .Пусть S<71, тогда координаты точки В, соответствующей оптимальному решению находятся из уравнения  при условии х2 =0. Следовательно,  .При уменьшении S от 71 до 0 оптимальная точка В будет перемещаться вдоль отрезка СО, тогда оптимальное решение будет иметь вид:  Согласно условию дополняющей нежесткости имеем: 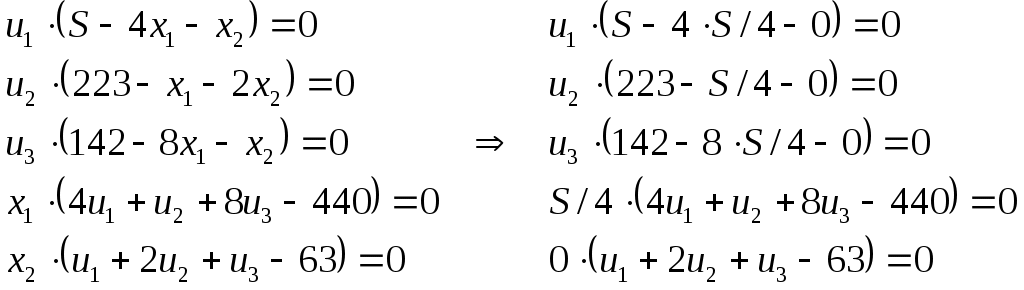 Так как  Так как  Так как  Имеем систему уравнений: 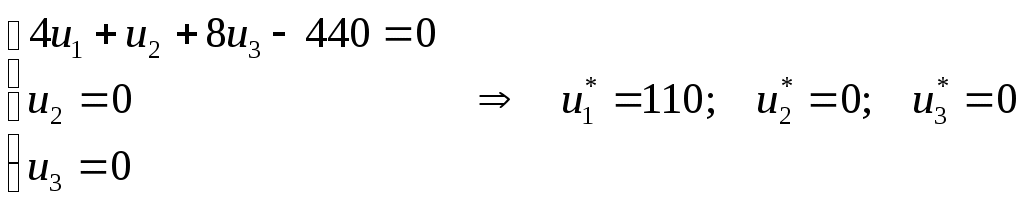 Следовательно,  .В итоге для всех возможных значений 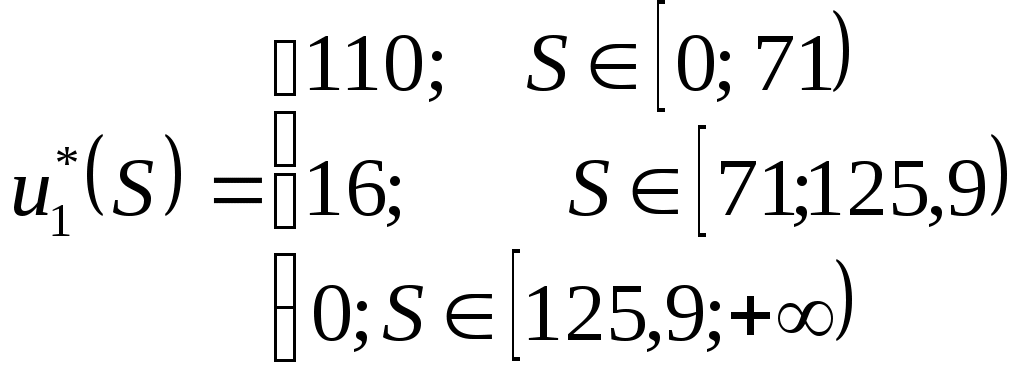 функция предельной полезности: График функции предельной полезности сырья изображен на рисунке 2. |
