РГР по ТММ. Задача Структурный анализ и кинематика рычажных механизмов
 Скачать 2.21 Mb.
|
|
Кинематическое и силовое исследование рычажного механизма. Расчетно-графическая работа состоит из двух задач и охватывают две основные разделы дисциплины: первая задача «Структурный анализ и кинематика рычажных механизмов», вторая задача «Динамика рычажных механизмов». Все графические построения строятся в масштабе на миллиметровке. Под масштабом в ТММ понимается как отношение действительного значения физической величины в свойственных ей единицах измерения (система СИ) к отрезку (в мм), изображающему её на чертеже. Такое понятие позволяет изображать в виде отрезков на чертеже любые параметры (линейные размеры, скорости, ускорения, силы и др.). Задача структурного анализа заключается в определении числа и вида подвижных звеньев, числа и вида кинематических пар, в разбивке механизма на группы Асура. Задачами кинематического анализа являются: 1. Построение плана положений механизма. 2. Определение положений звеньев и траекторий движения точек этих звеньев. 3. Определение угловых скоростей звеньев и линейных скоростей их точек. 4. Определение угловых ускорений звеньев и линейных ускорений их точек. Исходные данные для обеих задач приведены в таблицах 1 и 2, схемы рычажных механизмов в приложении 1.Варианты схем механизмов выбираются из приложения 1 по последней цифре шифра студента, а вариант числовых данных по последней цифре шифра из таблиц 1 и 2. 1.Решение задачи начинают с определения числа степеней подвижности механизма по формуле Чебышева для плоских механизмов: W = 3п'-2 p5- p4, гдеn'- число подвижных звеньев; p5 - количество кинематических пар V класса; p4-количество кинематических пар IV класса 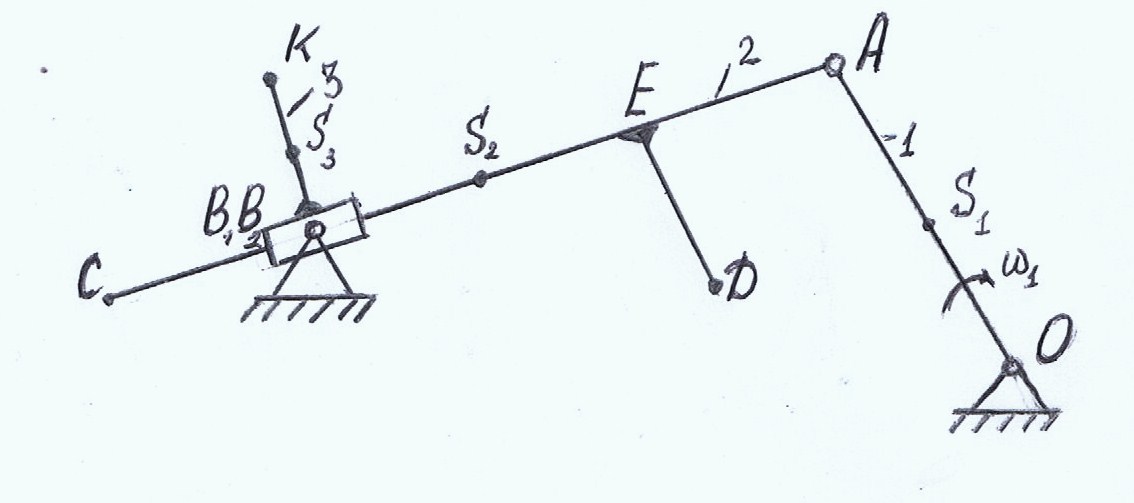  Рисунок 1- Кинематическая схема кривошипно-кулисного механизма 2. Затем нужно определить вид структурной группы (Ассура), присоединенной к начальному звену механизма, так как для каждого вида разработана своя методика кинематического и силового расчета. 2. План положений механизма. Планом положений механизма называют чертеж, построенный в масштабе  , представляющий собой ряд последовательных положений звеньев механизма, соответствующий полному циклу его движения. Непрерывные линии, соединяющие на плане последовательные положения одноименных точек, дают траектории движений этих точек.3. Планом скоростей (ускорений) механизма называют чертеж, построенный в масштабе  , на котором скорости (ускорения) различных точек изображены в виде векторов показывающих направления и величины этих скоростей (ускорений) в данный момент времени. На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана р (π). На конце вектора ставится строчная буква, соответствующая той точке механизма, которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет co6oй вектор относительной скорости соответствующих точек. Рассмотрим построение плана скоростей. 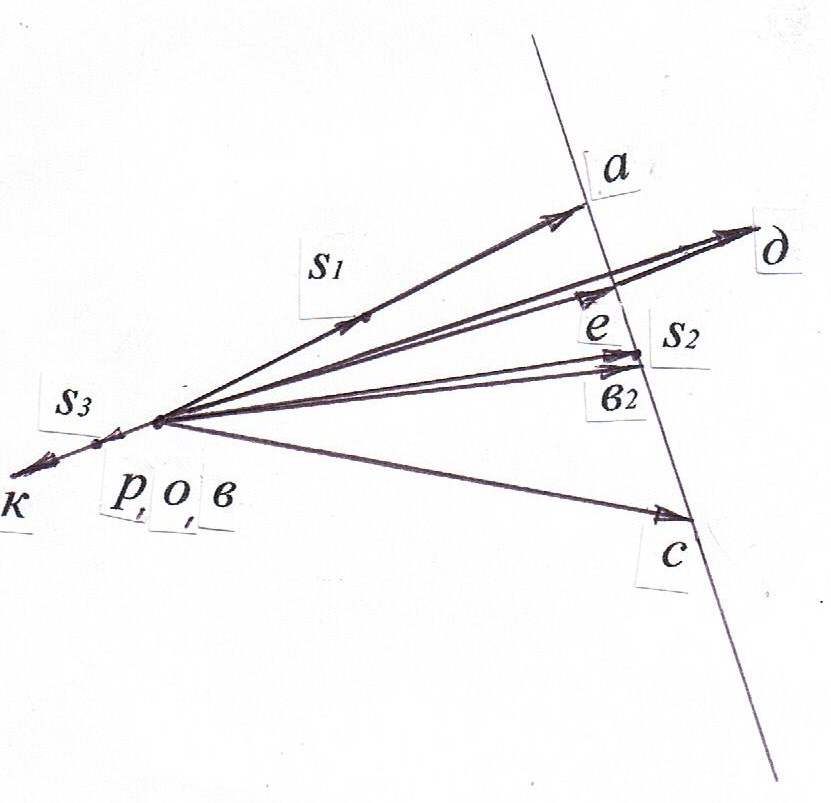  Рисунок 2- План скоростей 1) Рассмотрим построение плана скоростей для механизма представленного на рисунке 2. Кроме всех линейных размеров по условию задачи должна быть задана угловая скорость ведущего звена ω1 =const. Если задается частота вращения [n, об/мин], то ω1 =  . Поэтому скорость точки А определяется по формуле VA = ω1∙lOA. При этом    и направлена в сторону, соответствующую направлению угловой скорости звена ω1. Для присоединенной к начальному механизму выберем коэффициент масштабности   группе Ассура II класса 3 вида определим скорость точки В2 (точка В2 принадлежит направляющему звену и совпадает с шарниром ползуна В). Для этого составим два векторных уравнения:    (1)  (2)Построение плана скоростей ведется в такой последовательности: по векторным уравнениям (1) и (2) от полюса р откладывается отрезок ра, изображающий в масштабе скорость точки А (ра =  ). Затем из точки, а проводим направление относительной скорости  – линию перпендикулярную звену АС. Переходим к построению решения второго векторного уравнения из полюса р откладываем скорость точки В равную нулю (принадлежит стойке), т.е. точку в смещаем с точкой р. После этого из точки в проводим прямую до пересечения с перпендикулярной прямой к звену АВ и получаем искомую точку в2. Изобразим векторный отрезок соединяющий точку полюса р с в2. Вектор рв2 является вектором абсолютной скорости точки В2.  Скорость точки С определим из подобия, т.к. точки А ,В и С принадлежат одному и тому же звену:  Точку с откладываем на плане скоростей в продолжении звена АВ от точки в2. соединим точку полюса р с точкой с векторно и вычислим значение абсолютной скорости т.С :  Скорость т. Е определяется аналогично из подобия, т.к. принадлежит одному и тому же звену:  Отложим отрезок ае в мм. Соединим векторно точку полюса р с точкой е и вычислим абсолютную скорость точки: 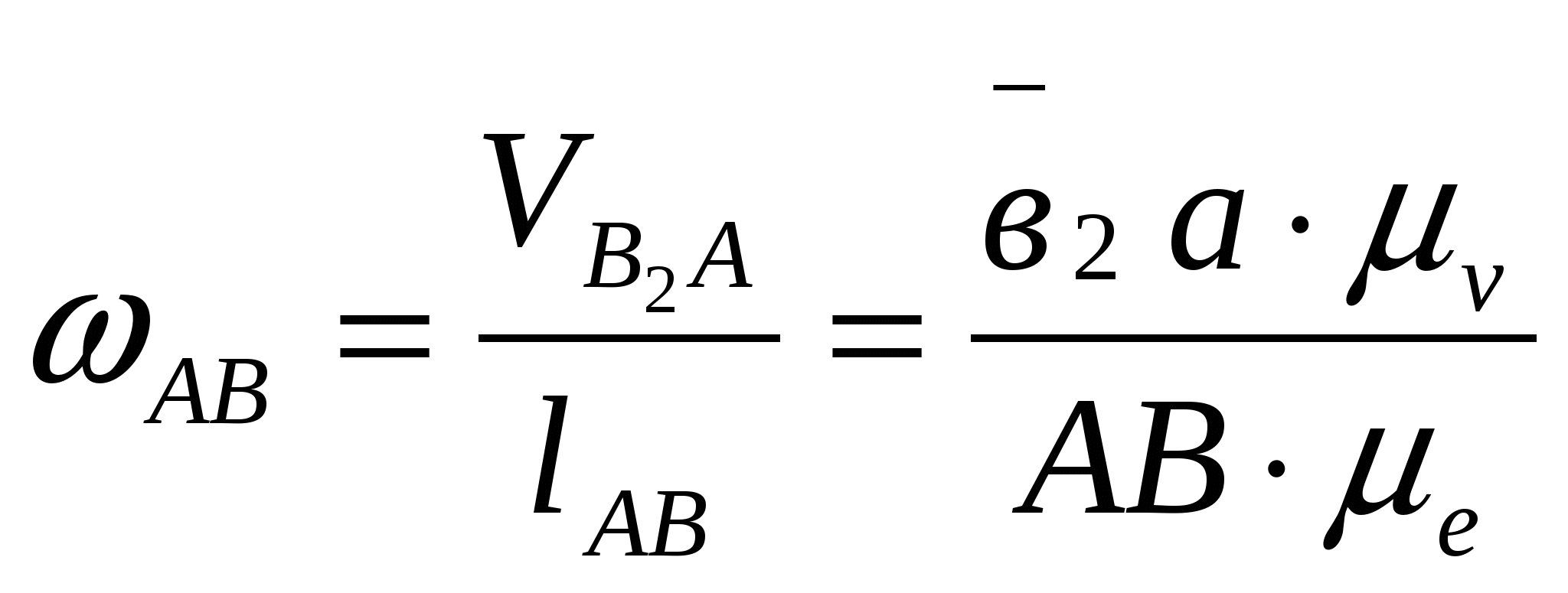  , где  и  – значения в масштабе. Скорость точки К нельзя определить используя условие подобия, т.к. точка принадлежит третьему звену. На 3 звене известна скорость только одной точки В (VB=0). Поэтому составим векторное уравнение:   ,      Скорость точки Д определим через скорость т.Е. Для этого составим векторное уравнение:     Далее определим положения центров масс S на плане скоростей и соединив векторно вычислим их абсолютные значения скоростей с точкой полюса  .2) Построение плана ускорений ведется в такой же последовательности. Для определения ускорения точки В2 запишем два векторных уравнения:  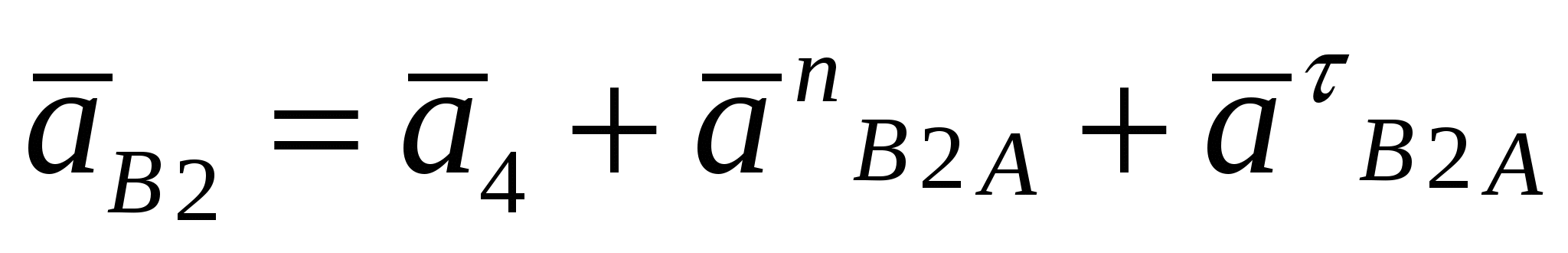 ,  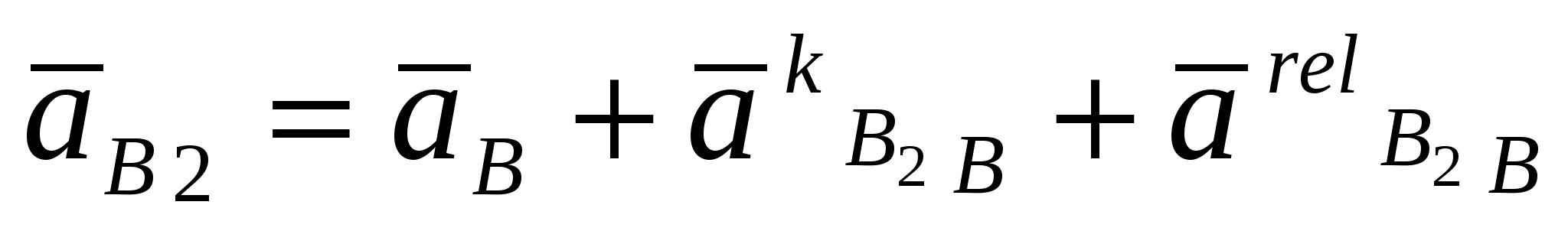 (направлено от точки А к точке О). Нормальное ускорение:  - (направлено от точки В2 к точке А). Касательное ускорение: 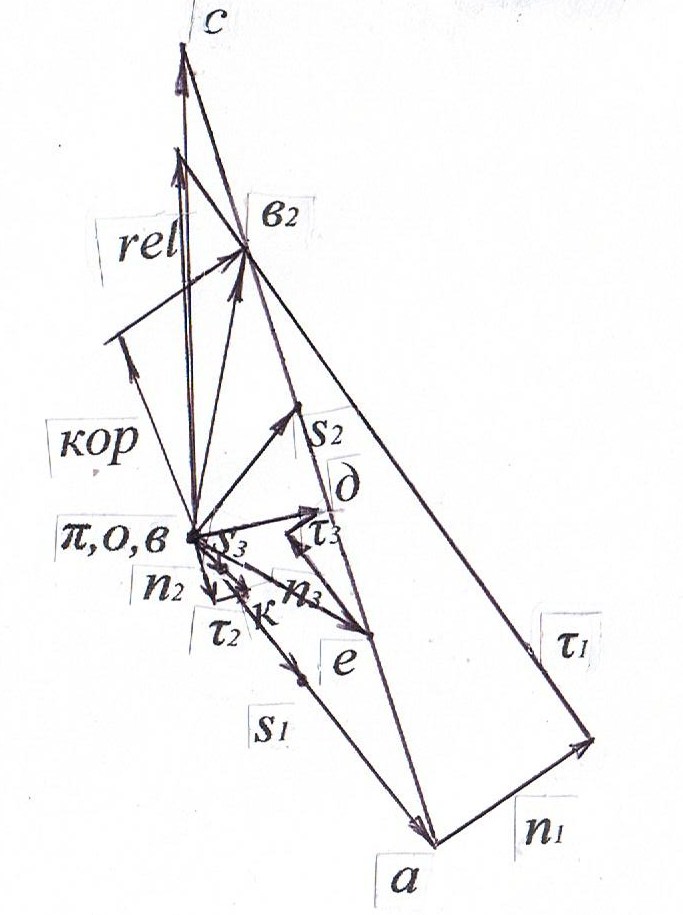 , направленно перпендикулярно  значение определить не можем, т.к. не известно    (принадлежит к стойке).  Рисунок 3 План ускорений механизма Ускорение Кориолиса по модулю равно:   . для определения его направления необходимо вектор скорости 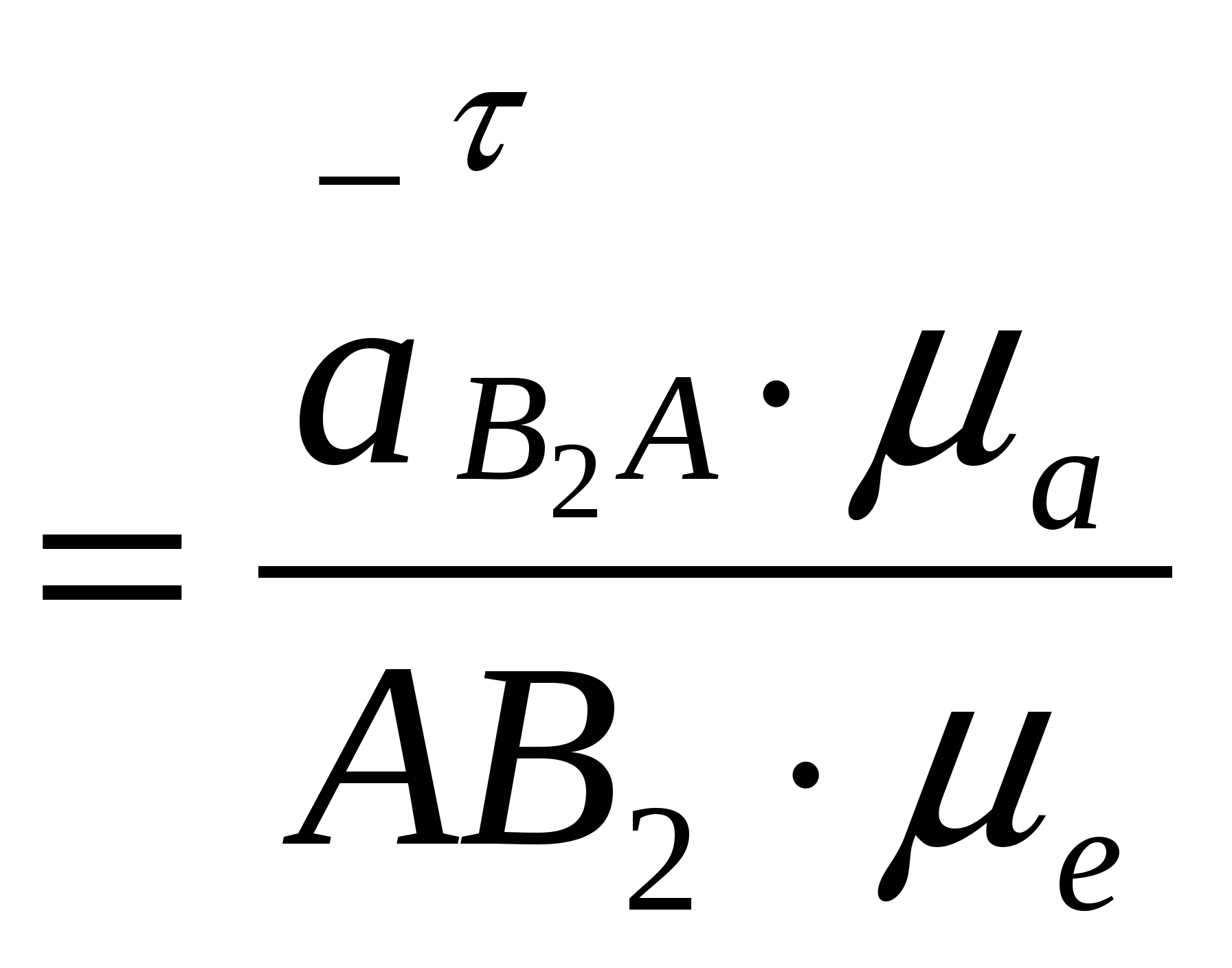 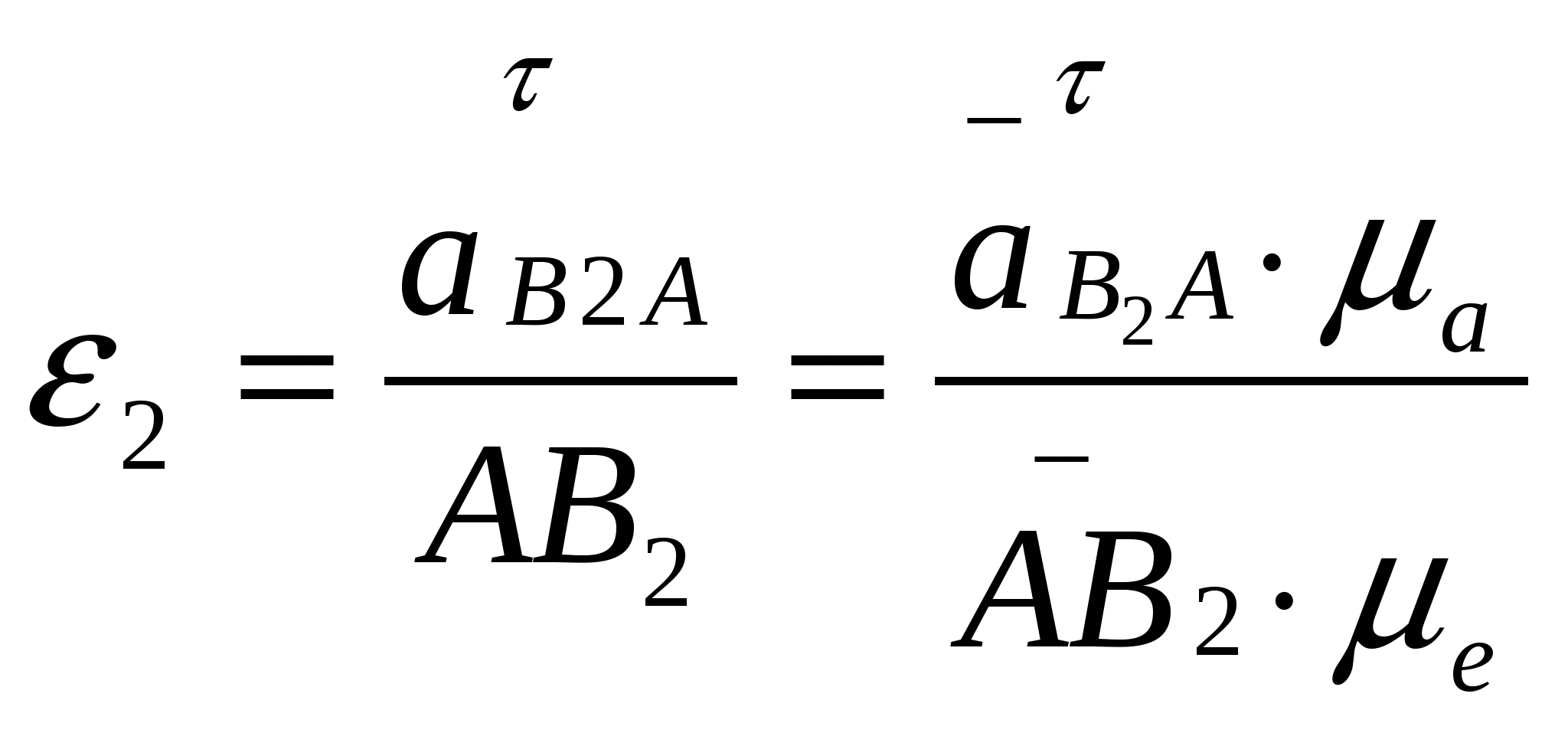на плане скоростей повернуть в сторону вращения АВ. После нахождения точки в2 на плане ускорений можно определить угловое ускорение второго звена ( ).   Релятивистское ускорение направлено вдоль направляющей ползуна, т.е.параллельно звену АВ:  Точка пересечения с тангенсальным и релятивистским ускорениями будет являться ускорением точки В2. Соединим векторно точку полюса π с точкой в 2 и вычислим абсолютное ускорение точки.  Для определения ускорений точек С и Е применим подобие (см. план скоростей) Определим ускорение точки К:  Так как все слагаемые известны по направлениям и значениям (   ;  второго уравнения не требуется.  Определим ускорение точки Д:   (направлено от точки Д к точке Е) (направлено перпендикулярно к нормальному ускорению)Соединим точку полюса π с точкой д .Определим абсолютное ускорение точки Д:  Далее определим положения центров масс (S) из подобия, соединив векторно с точкой полюса, вычислим их абсолютные ускорения. 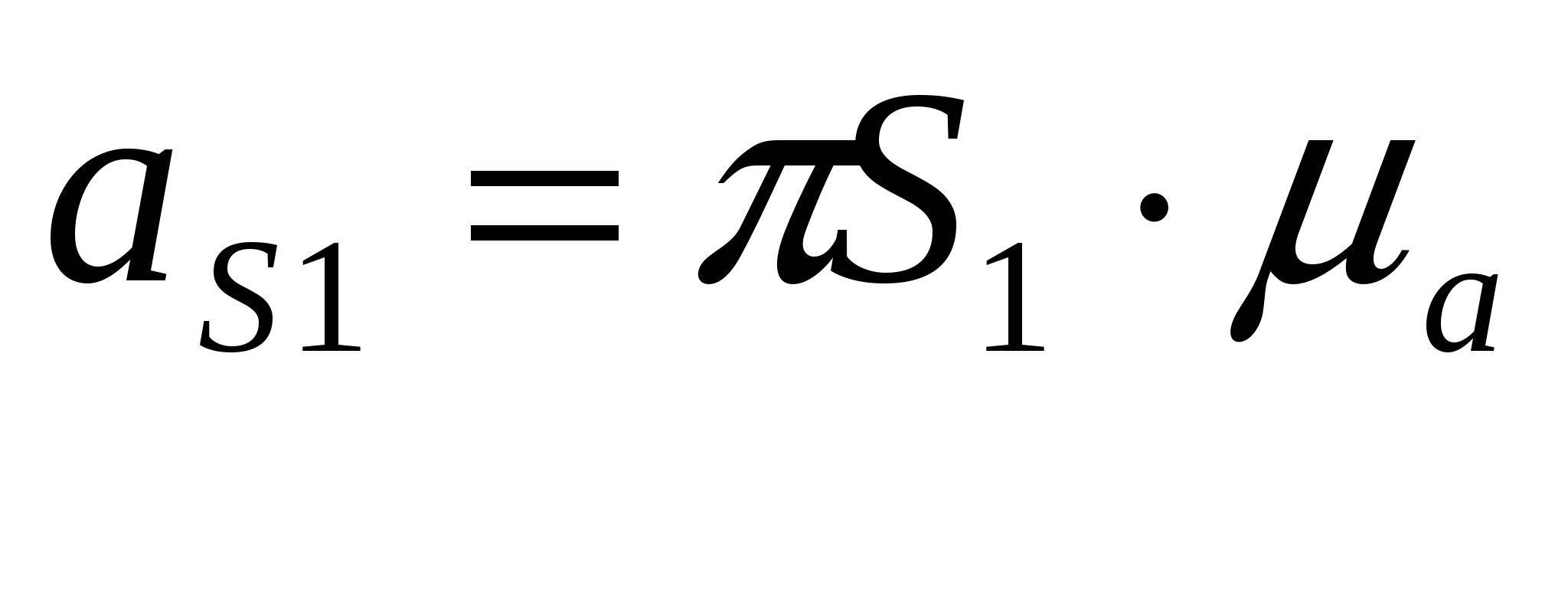  2. При выполнении силового расчета по методу Н.Е. Бруевича используют принцип кинетостатики: если ко всем внешним действующим на звенья механизма силам добавить силы инерции и моменты сил инерций, то механизм будет находиться в состоянии статического равновесия. Силовой расчет проводится по группам Ассура, начиная с наиболее отдалённой структурной группы (в случае, если их несколько) от начального механизма. Заканчивается решение расчетом кривошипа, входящего начальный механизм, для которого определяют уравновешивающий момент. Некоторые свойства планов скоростей и ускорений.
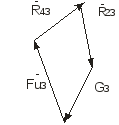
 3) Силовой расчет методом планов рассмотрим на примере механизма, рассмотренного в предыдущей задаче. Силу инерции звеньев (  ) необходимо направить противоположно направлениям центрам масс звеньев. Инерционные моменты ( где  - момент инерции масс звена 1 относительно центральной оси), направляются против угловых ускорений ( .Для того чтобы механизм находился в равновесии под воздействием всех сил к ведущему звену должен быть приложен уравновешивающий момент или уравновешивающая сила. Силовой расчет следует начинать с группы Ассура, присоединенной к механизму при его образовании в последнюю очередь. В данном примере от механизма может быть отделена только одна группа. Это структурная группа II класса 3 вида. Группу Ассура начертим отдельно в масштабе (рисунок 4). 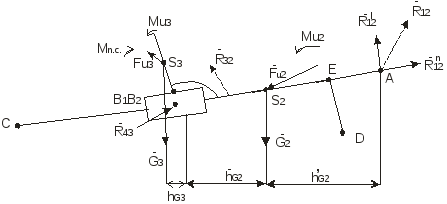= м/мм Рисунок 4 Силовой расчет для группы Ассура 2 класса 3 вида. При этом в кинематических парах А и В прикладываем реакции R12 и R43, которые неизвестны ни по величине, ни по направлению. Одну из реакций (например, R12) разложим на две составляющих:  , направленную перпендикулярно линии АВ, и  , направленную параллельно линии АВ. Затем составляем следующие уравнения равновесия.
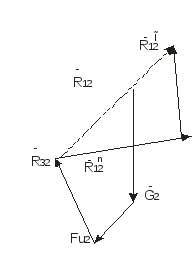   Рисунок 5 План сил
 При решении уравнения (1) плечи h измеряем на чертеже в мм и умножаем на коэффициент масштабности μl . При построении плана сил по уравнению (2) вначале проводим направление неизвестной по величине реакции  , а затем, с любой точки на этой прямой, откладываем вектора согласно уравнению (2). Направление последней реакции  проводим с конца предпоследнего слагаемого  , до пересечения с направлением . Для определения модулей неизвестных реакций полученные вектора умножаем на масштаб плана сил. Решая уравнения (3) находим точку приложения реакции R32 в поступательной паре. При этом плечи h и h' по уравнениям (1) и (3) отличается, т.к. моменты составлены относительно разных точек "B" и "А". Решая уравнение (4) реакции  , определяем и по величине и по направлению (при этом необходимо помнить что ).В заключение проводим силовой расчет ведущего звена 1:
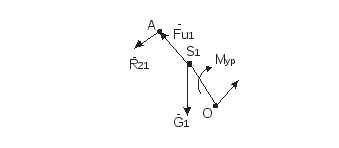 Рисунок 6 Кинетостатика ведущего звена 2) 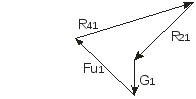  Рисунок 7 План сил Вариант схемы механизмов выбирается по предпоследней цифре шифра студента, а вариант числовых данных – по последней цифре шифра. ЗАДАЧИ 1 И 2 Варианты схем механизмов выбираются из рисунков 1, 2, 3, а числовые данные и соотношения звеньев – из таблиц 1 и 2 Таблица 1
Таблица 2
Примечание – центр масс звена ОА во всех вариантах OS1= 0,5∙ОА ПРИЛОЖЕНИЕ 1 (обязательное) 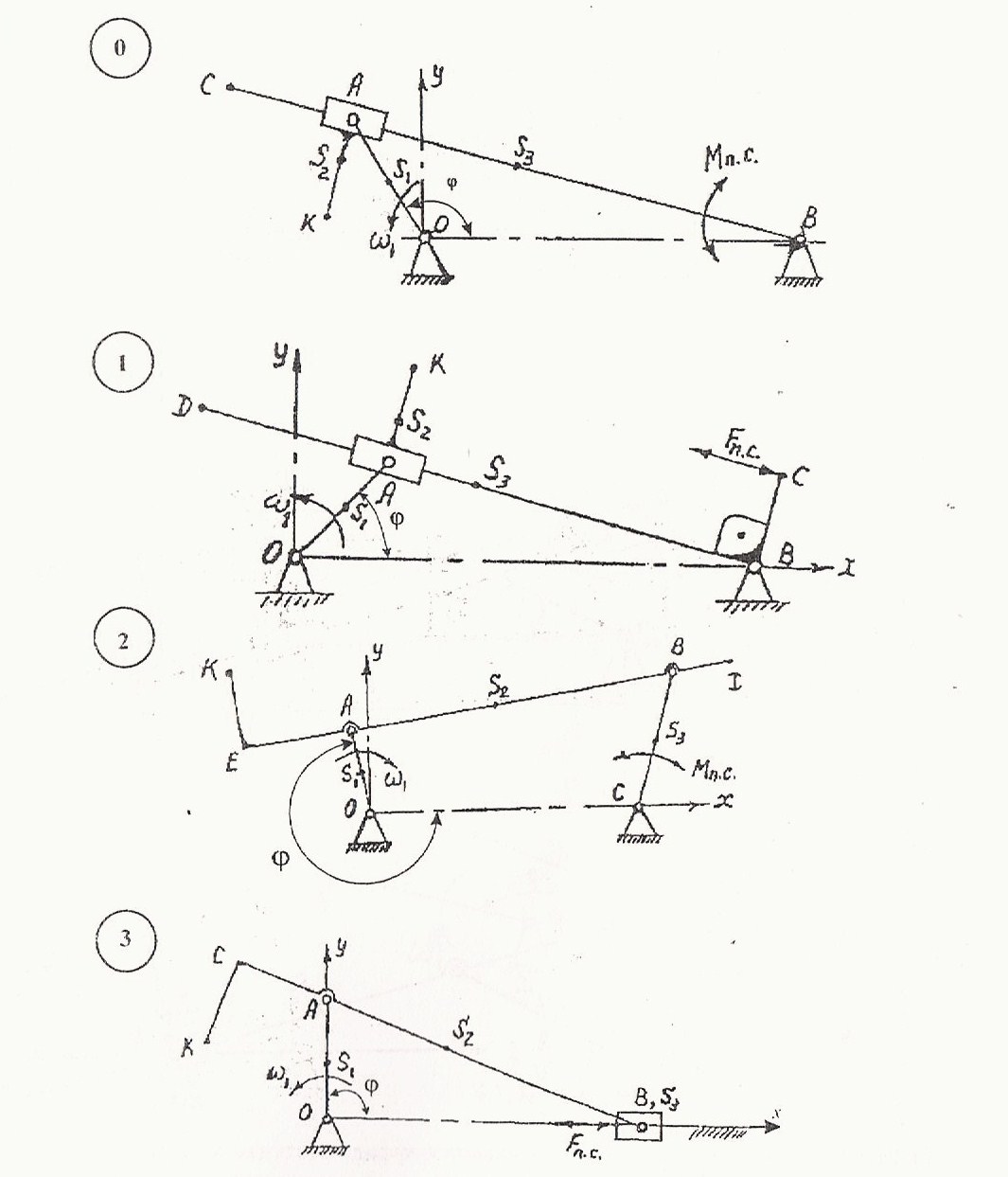 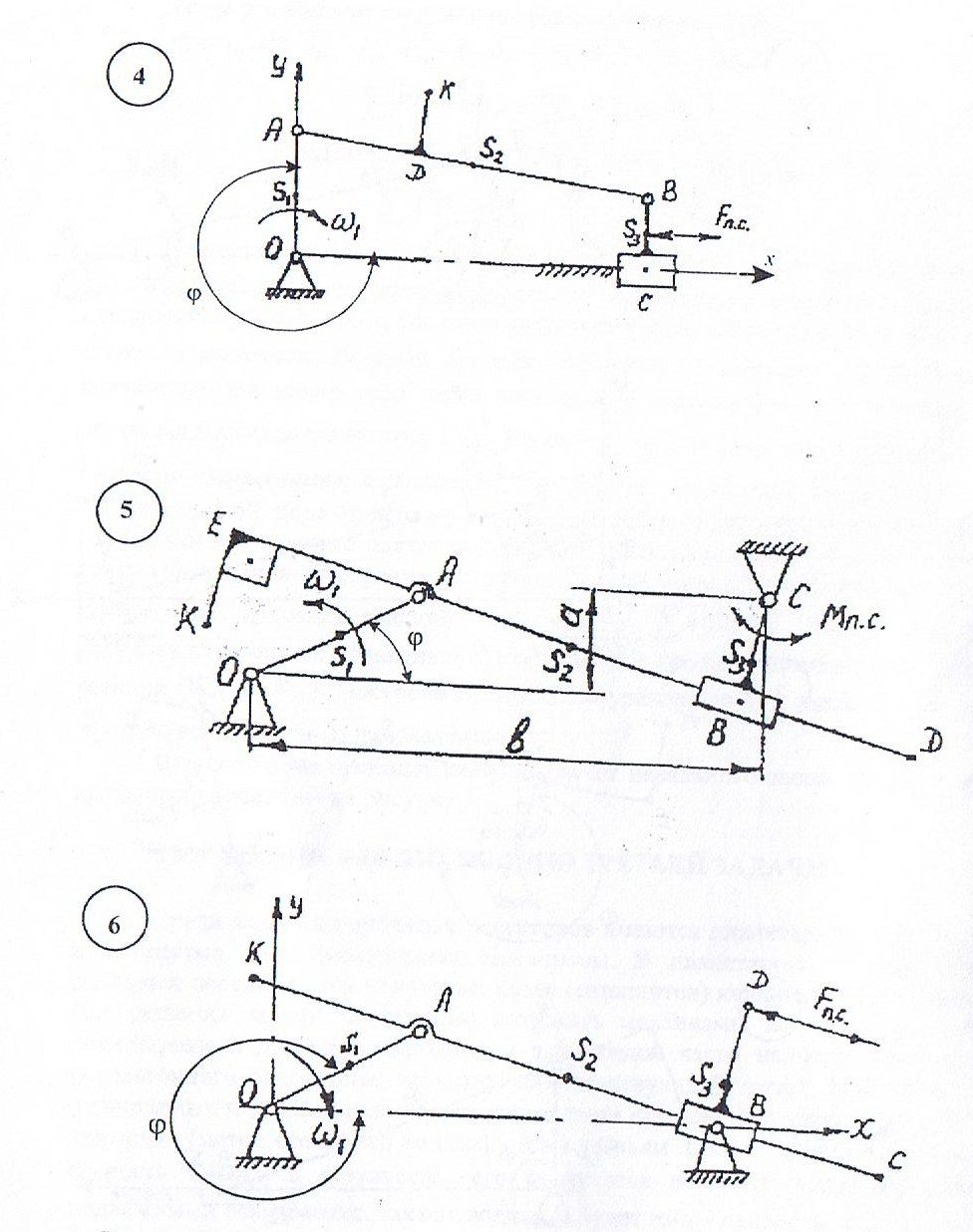 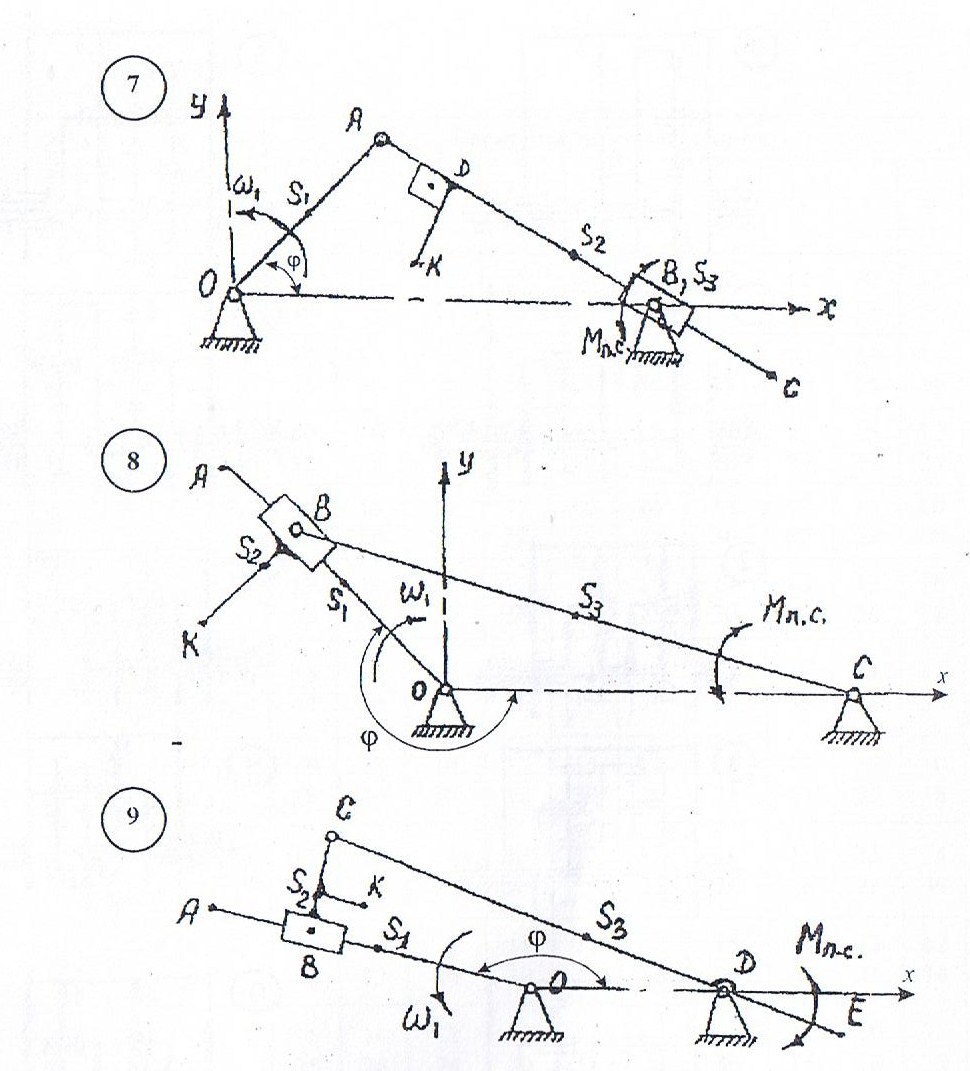 ПРИЛОЖЕНИЕ 2 (обязательное) 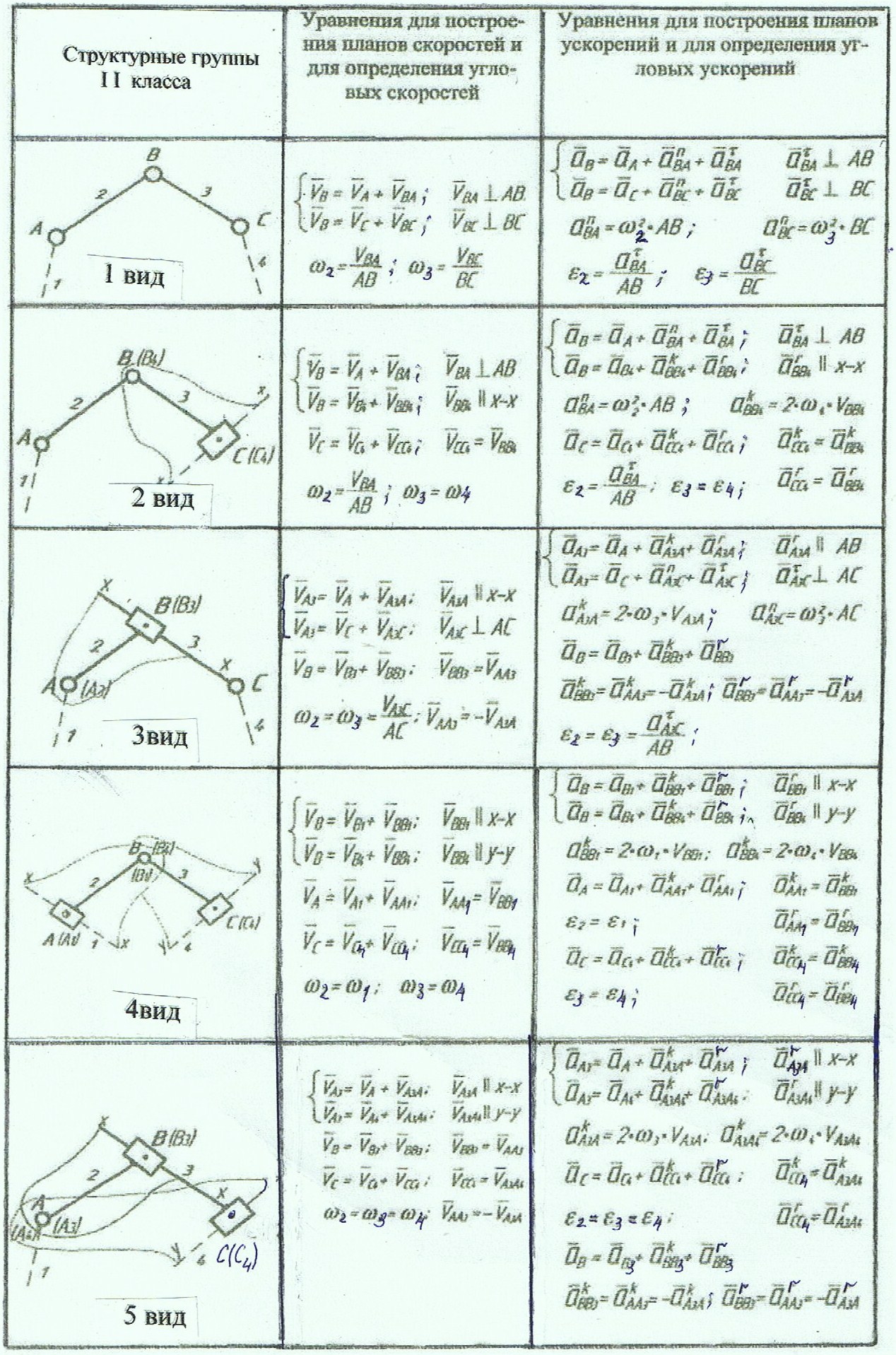 ПРИЛОЖЕНИЕ 3 (обязательное) 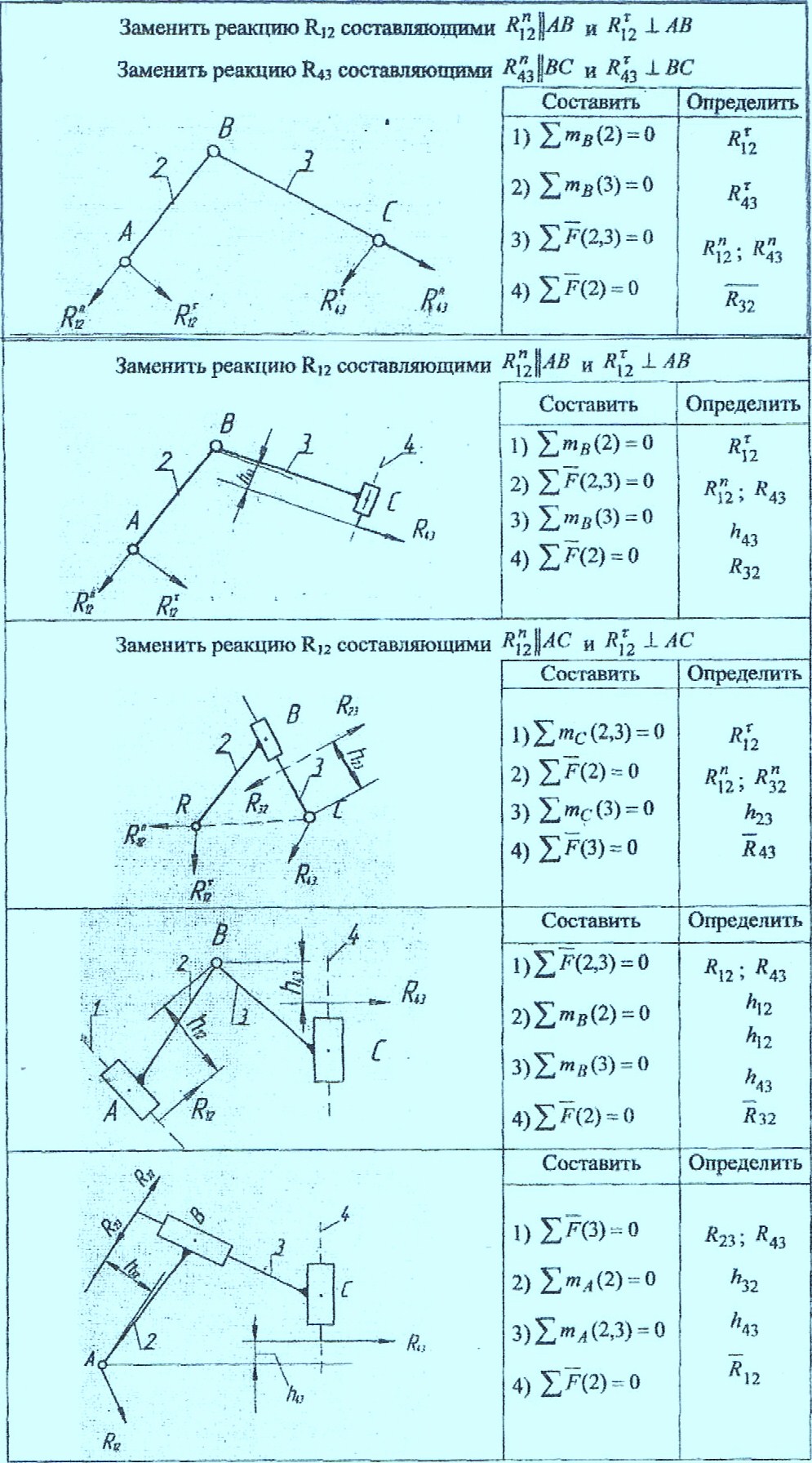 Рекомендуемая литература:
1989. – 366 с.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определим 
.
определим 
.
определим h32.
определим R43.
;
, рад/с
, град
, кг