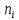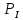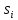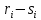Тер вер вар 14. ТВиМС КР2. Задача Тема Нормальное распределение
 Скачать 60.71 Kb. Скачать 60.71 Kb.
|
|
Задача 1. Тема: «Нормальное распределение» Технический отдел компании, производящей автопокрышки, планирует выпустить несколько партий покрышек и проверить степень их износа на тестирующем оборудовании. С этой целью предполагается увеличивать количество каучука в покрышках каждой последующей партии до тех пор, пока срок службы покрышек окажется приемлемым. Эксперимент показал, что стандартное отклонение срока службы покрышек фактически остается постоянным от партии к партии и составляет 2500 миль. Если компания хочет, чтобы 80% выпускаемых покрышек имели срок службы не менее 2500 миль, то какой наименьший средний срок службы автопокрышек должен быть заложен в расчетах технического отдела. Считать срок службы автопокрышек нормально распределенным. Решение: σ = 2500; γ = 0,8; Вероятность попадания в заданный интервал равна: 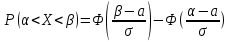 ; ;Тогда получим: 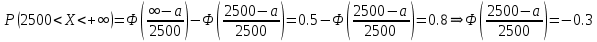 По таблице значений функции Лапласа получим:   Ответ: a = 4612 миль. Задача 2. Тема: «Интервальные оценки» Среднемесячный бюджет студентов в колледжах одного из штатов США оценивается по случайной выборке. С вероятностью 0.9 найдите наименьший объем выборки, необходимый для такой оценки, если среднее квадратичное отклонение предполагается равным 100 у.е., а предельная ошибка средней не должна превышать 20 у.е. Решение: 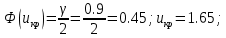  Используя формулу  получим: получим: Ответ: объем минимальной выборки  . .Задача 3. Тема: «Проверка статистических гипотез» Инженер по контролю качества проверяет среднее время горения нового вида электроламп. Для проверки случайным образом было отобрано 100 ламп, среднее время горения которых составило 1075 часов. Предположим, что среднее квадратичное отклонение времени горения для генеральной совокупности известно и составляет 100 часов. На уровне значимости α = 0.01 проверьте гипотезу о том, что среднее время горения ламп более 1000 часов. Решение: Согласно алгоритму проверки статистических гипотез, сформулируем основную и альтернативные гипотезы. Основная гипотеза 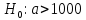 – время горения ламп более 1000 часов. – время горения ламп более 1000 часов.Альтернативная гипотеза 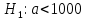 – время горения ламп менее 1000 часов. – время горения ламп менее 1000 часов.По выборке и формуле критерия K рассчитаем 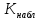  В зависимости от вида 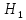 определяют вид критической области и критические точки. Так как определяют вид критической области и критические точки. Так как 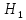 левостороннее, то и критическая область левосторонняя и её границу левостороннее, то и критическая область левосторонняя и её границу  следует искать по таблице функции Лапласа. следует искать по таблице функции Лапласа. Наблюдаемое значение (  ) попало в критическую область т.к. ) попало в критическую область т.к.  , следовательно основная гипотеза отвергается в пользу альтернативной. , следовательно основная гипотеза отвергается в пользу альтернативной.Ответ: Время горения ламп в среднем менее 1000 часов. Задача 4. Тема: «Критерий согласия Пирсона» С помощью критерия согласия Пирсона на уровне значимости α = 0,05 выяснить, можно ли считать случайную величину X, заданную в виде сгруппированного статистического ряда, нормально распределенной с параметрами и s, рассчитанными по выборке.
Решение: Определим середину для каждого интервала:
Общее число значений n:  Вычислим выборочное среднее:  Вычислим выборочную дисперсию: 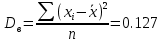  Вероятность попадания случайной величины в каждый интервал равна приращению функции распределения:  ; ;Теоретические частоты вычислим по формуле: 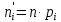 Вычислим значения:  Результаты занесем в таблицу:
Получим: 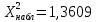 Число степеней свободы:  По таблице  при уровне значимости при уровне значимости 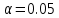 находим находим 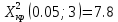 . .Так как 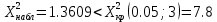 , то нет основания отвергать гипотезу о нормальном распределении. , то нет основания отвергать гипотезу о нормальном распределении.Ответ: нет оснований отвергать гипотезу о нормальном распределении. Задача 5. Тема: «Ранговая корреляция» По заданной таблице рангов найти выборочный коэффициент ранговой корреляции Спирмена и проверить значимость полученного результата при α = 0.05. Десять студентов четвертого курса проранжированы по двум признакам: X - средний балл на первом курсе, Y - средний балл на четвертом курсе.
Построим ранговую таблицу
  Проверим значимость полученного результата при 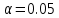 . Сформулируем основную и альтернативную гипотезы. . Сформулируем основную и альтернативную гипотезы.Основная гипотеза  – между X и Y нет линейной связи. – между X и Y нет линейной связи.Альтернативная гипотеза 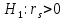 – между переменными X и Y есть линейная связь. – между переменными X и Y есть линейная связь.Наблюдаемое значение статистики K равно:  Альтернативная гипотеза 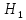 является правосторонней. По уровню значимости является правосторонней. По уровню значимости 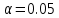 и числу степеней свободы и числу степеней свободы  , по таблице приложения критических точек распределения Стьюдента находим критическую точку , по таблице приложения критических точек распределения Стьюдента находим критическую точку  2.31. 2.31.Наблюдаемое значение 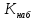 не попадает в критическую область не попадает в критическую область  поэтому нет оснований отвергать основную гипотезу в пользу альтернативы. поэтому нет оснований отвергать основную гипотезу в пользу альтернативы.Ответ: Данные наблюдений на уровне значимости 0,05 говорят о том, что средний балл на первом курсе оказывает не существенное влияние на средний балл на четвертом курсе. Задача 6. Тема: «Линейная корреляция и регрессия» Для приведенных исходных данных постройте диаграмму рассеяния и определите по ней характер зависимости. Рассчитайте выборочный коэффициент корреляции Пирсона, проверьте его значимость при α = 0.05. Запишите уравнение регрессии и дайте интерпретацию полученных результатов. Исследуется зависимость производительности труда (X, шт.) от коэффициента механизации работ (Y, %) по выборке из 14 предприятий одного типа.
Решение: Построим диаграмму рассеяния:  По виду диаграммы есть основания полагать линейную зависимость между производительностью труда и коэффициентом механизации работ т.е. уравнение регрессии будет иметь вид  . .Для расчета коэффициента регрессии найдем промежуточные значения. Средние значения: 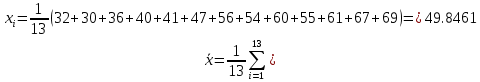  Несмещенные оценки дисперсий:  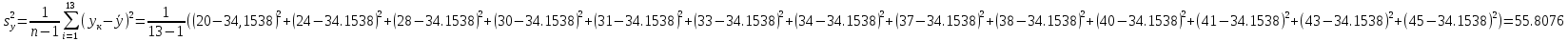 Оценка коэффициента корреляции Пирсона: 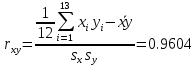 Близость коэффициента корреляции к единице свидетельствует о тесной положительной линейной связи между производительностью труда и коэффициентом механизации работ. Рассчитаем теперь оценки коэффициентов регрессии:  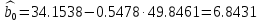 Таким образом, уравнение регрессии Y на X имеет вид:  Рассчитаем выборочный коэффициент корреляции Пирсона и проверим его значимость при 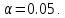  Число степеней свободы 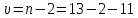 . По таблице критических точек распределения Стьюдента находим . По таблице критических точек распределения Стьюдента находим  . .Так как  , то коэффициент корреляции значим. , то коэффициент корреляции значим. Коэффициент  характеризует наклон линии регрессии, и значение характеризует наклон линии регрессии, и значение  =0.5478 показывает, что при увеличении X на единицу ожидаемое значение Y возрастет на 0,5478. Регрессионная модель указывает на то, что при увеличении коэффициента механизации работ на 1% производительность труда увеличивается на 0,548шт. т.е. при 100% увеличится на 548шт. Отсюда =0.5478 показывает, что при увеличении X на единицу ожидаемое значение Y возрастет на 0,5478. Регрессионная модель указывает на то, что при увеличении коэффициента механизации работ на 1% производительность труда увеличивается на 0,548шт. т.е. при 100% увеличится на 548шт. Отсюда  может интерпретироваться как прирост производительности труда в зависимости от коэффициента механизации работ. может интерпретироваться как прирост производительности труда в зависимости от коэффициента механизации работ. Свободный член 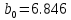 в уравнении регрессии это значение Y при X = 0. в уравнении регрессии это значение Y при X = 0. |