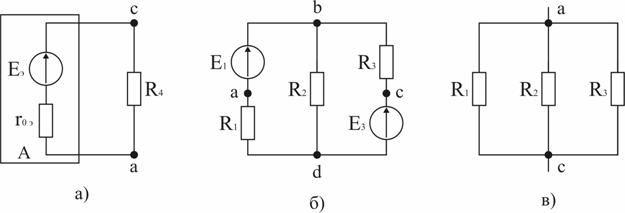
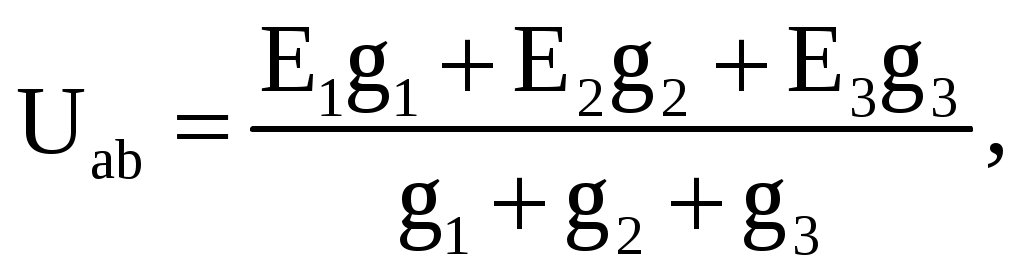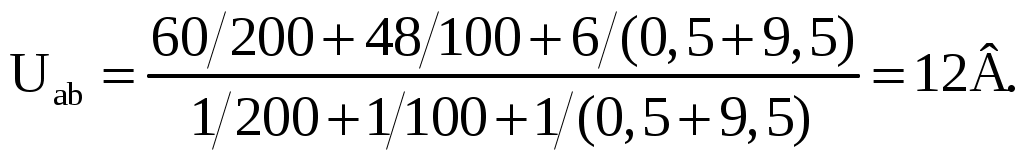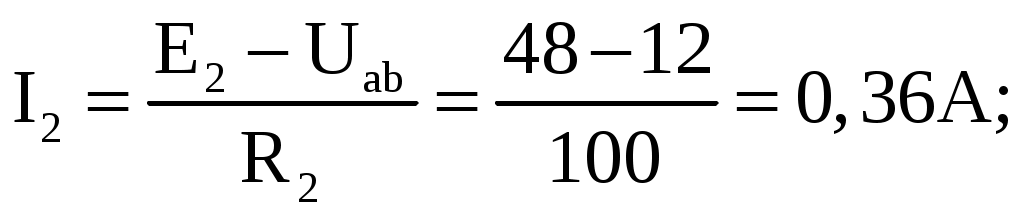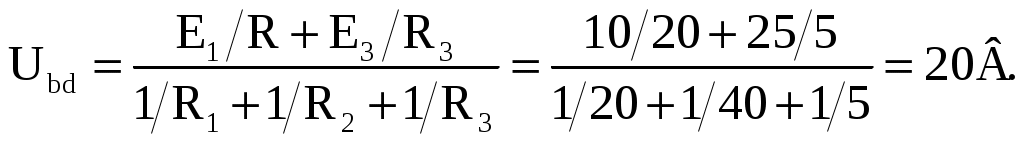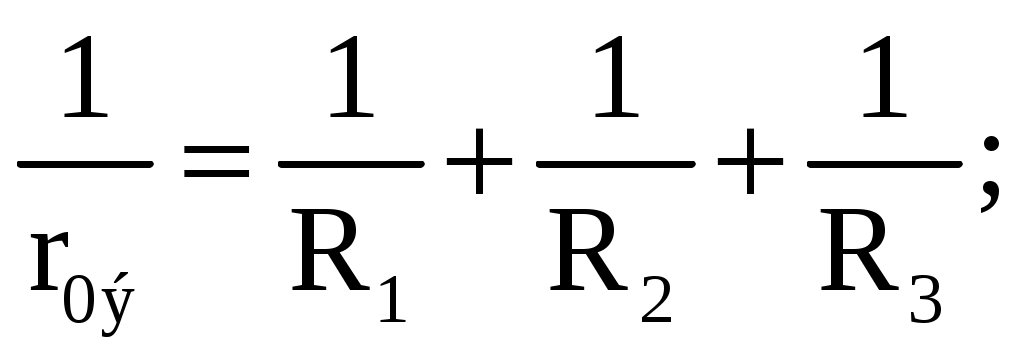ПОСТ ПРАКТИКА. Задача в цепи, схема которой приведена на рис. 29, Эдс аккумуляторной батареи е 78 В, ее внутреннее сопротивление r

• Название: Задача в цепи, схема которой приведена на рис. 29, Эдс аккумуляторной батареи е 78 В, ее внутреннее сопротивление r
• Дата: 22.04.2022
• Размер: 124 Kb.
• Имя файла: ПОСТ ПРАКТИКА.doc
• Тип: Задача; #490317

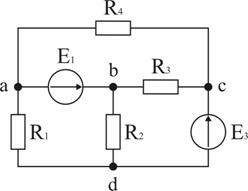
Примеры расчета цепей постоянного тока

2.9.1. Расчет цепи с одним источником питания

Задача 1. В цепи, схема которой приведена на рис. 2.29, ЭДС аккумуляторной батареи Е = 78 В, ее внутреннее сопротивление r₀ = 0,5 Ом. Сопротивления резисторов R₁ = 10 Ом, R₂ = 5 Ом, R₃ = 4 Ом. Вычислить токи во всех ветвях цепи и напряжения на зажимах батареи и на каждом их резисторов.

Проанализировать как изменятся токи в схеме при увеличении сопротивления резистора R_1.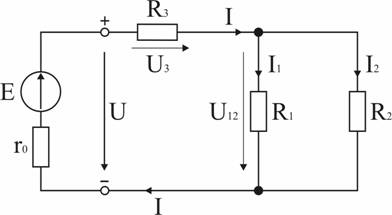

Рис. 2.29. Расчетная схема

Анализ и решение задачи 1.

1. Обозначение токов и напряжений на участках цепи.

Резистор R₃ включен последовательно с источником, поэтому ток I для них будет общим, токи в резисторах R₁ и R₂ обозначим соответственно I₁ и I₂. Аналогично обозначим напряжения на участках цепи.

2. Определение эквивалентного сопротивления цепи:

R_э = r₀ + R₃ + R₁ R₂ / (R₁ + R₂) = 0,5 + 4 + 5 10 / (5 +10) = 7,8 Ом

3. Ток в цепи источника рассчитываем по закону Ома:

I = E / R_э = 78 / 7,8 = 10 А.

4. Определение напряжений на участках цепи:

U₁₂ = R₁₂ I = 3,3 10 = 33 В; U₃ = R₃ I = 4 10 = 40 В;

U = E − r₀ I = 78 − 0,5 10 = 73 В.

5. Определение токов и мощностей всех участков:

I₁ = U₁₂ / R₁ = 33 / 10 = 3,3 А; I₂ = U₁₂ / R₂ = 33 / 5 = 6,6 А;

P₁ = R₁ I₁² = U₁₂ I₁ = 108,9 Вт; P₂ = R₂ I₂² = U₁₂ I₂ = 217,8 Вт;

P₃ = R₃ I² = U₃ I = 400 Вт.

Мощность потерь на внутреннем сопротивлении источника

ΔP = r₀ I² = 50 Вт.

Мощность источника питания P = E I = 780 Вт.

6. Проверка правильности решения задачи.

Правильность вычисления токов можно проверить, составив уравнение на основании первого закона Кирхгофа: I = I₁ + I₂; 10 − 3,3 − 6,6≈0.

Правильность расчета мощностей проверяют по уравнению баланса мощностей:

P = P₁ + P₂ + P₃ + ΔP.

Подставим числа:

Р=780 Вт, P₁ + P₂ + P₃ + ΔP +108,9 + 217,8 +400 + 50 =776,7 Вт.

Видно, что имеет место приближенное равенство.

7. Как изменятся токи в схеме при увеличении R₁?

При увеличении R₁ увеличивается сопротивление параллельного участка схемы R₁₂, поэтому увеличивается сопротивление R_экв, что приводит к уменьшению тока I. При уменьшении I уменьшаются падения напряжения I R₃ и I r₀ и, в соответствии со вторым законом Кирхгофа, напряжение на разветвлении U₁₂ = E − I (R₃ + r₀) возрастает, что приводит к увеличению тока в резисторе R₂. Т.к. ток I уменьшается, а ток I₂ возрастает, ток I₁ = I − I₂ уменьшается.

2.9.2. Расчет сложных цепей при помощи уравнений Кирхгофа

Задача 2. Рассчитать схему рис. 2.30, составив систему уравнений на основании законов Кирхгофа.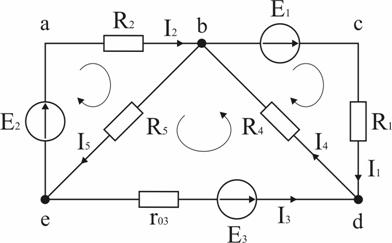

Рис. 2.30. Расчетная схема
Исходные данные к задаче 2:

E₁ = 60 В; E₂ = 80 В; E₃ = 70 В;

R₁ = 20 Ом; R₂ = 50 Ом; r₀₃ = 5 Ом; R₄ = 65 Ом; R₅ = 85 Ом.

Анализ и решение задачи 2

1. Определение необходимого числа уравнений.

В схеме рис. 2.30 пять ветвей и для расчета токов в них надо составить пять уравнений. По первому закону Кирхгофа составляются уравнения для всех узлов, кроме одного (уравнение для него будет следствием предыдущих), по второму – для независимых контуров (в каждый последующий контур входит хотя бы одна ветвь, не вошедшая в ранее рассмотренные). Для данной схемы надо составить два уравнения по первому закону и три – по второму.

2. Составление и решение системы уравнений.

Для составления уравнений задаемся произвольно направлениями токов в ветвях и направлениями обхода контуров (рис. 2.30).

Уравнение для узла d: I₁ + I₃ − I₄ = 0.

Уравнение для узла е: − I₂ − I₃ + I₅ = 0.

Уравнение для контура bcd: I₁R₁ + I₄R₄ = E_2.

Уравнение для контура abe: I₂R₂ + I₅R₅ = E₂.

Уравнение для контура bde: I₃r₀₃ + I₄ R₄ + I₅R₅ = E₃.

Подставив в уравнения численные значения величин, получим алгебраическую систему уравнений:

I₁ + I₃ − I₄ = 0;

− I₂ − I₃ + I₅ = 0;

20 I₁ + 65 I₄ = 60;

50 I₂ + 85 I₅ = 80;

5 I₃ + 65 I₄ + 85 I₅ = 70.

Решение системы дает значения токов:

I₁ = 1,093 А; I₂ = 0,911 А;

I₃ =  – 0,506 А; I₄ = 0,587 А; I₅ = 0,405 А.

Ток I₃ имеет знак минус перед численным значением тока. Знак «–» говорит о том, что реальное направление тока в данной ветви противоположно принятому в начале расчета.

3.  Режимы работы элементов схемы, содержащих источники ЭДС. В ветвях с E₁ и E₂ токи совпадают по направлению с ЭДС, т.е. данные элементы работают источниками, отдавая энергию в схему; в ветви с ЭДС E₃ ток направлен против ЭДС, т.е. данный элемент работает потребителем (например, машина постоянного тока в режиме двигателя).

4. Проверка правильности решения задачи.

Для проверки правильности расчета можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы. Независимой проверкой является уравнение баланса мощностей: сумма мощностей источников P_ист  равна сумме мощностей, расходуемых в резистивных элементах схемы мощности потребителей P_потр. Т.к. элемент схемы с ЭДС может работать как в режиме источника, так и в режиме потребителя, соответствующее слагаемое в левой части уравнения берется с плюсом, если Е и I совпадают по направлению (источник), и с минусом, если направления противоположны (потребитель).

4.1. Проверка расчетов по первому закону Кирхгофа.

При решении задачи не использовался узел b. Запишем уравнение для этого узла (рис. 2.30):

I₂ + I₄ – I₅ – I₃ = 0,911 + 0,587 –0,405 – 1,053 = 0,054≈ 0.

4.2. Проверка расчетов по балансу мощностей.

Мощности элементов схемы с ЭДС:

P_ист = E₁I₁+ E₂I₂ − E₃I₃ = 60 1,093 + 80 0,911 − 70 0,506 = 104,04 Вт.

Мощности, расходуемые в резистивных элементах схемы:

P_потр.= R₁I₁² + R₂I₂² + r₀₃I₃² + R₄I₄²+ R₅I₅² = 20∙1,093² + 50∙0,911² + 5∙0,506² + 65∙0,587² + 85∙0,405² = 103,01 Вт.

P_потр.≈ P_ист

Баланс мощностей практически сошелся, следовательно, задача решена верно.

2.9.3. Расчет цепи методом узлового напряжения

Задача 3. В схеме рис. 2.31 E₁ = 60 В, E₂ = 48 В, E₃ = 6 В, R₁ = 200 Ом, R₂ = 100 Ом, r₀₃ = 0,5 Ом, R₃ = 9,5 Ом. Определить токи в ветвях схемы.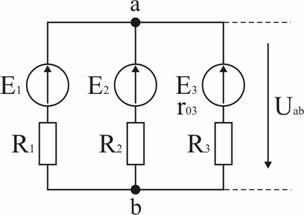



Рис. 2.31. Расчетная схема

Анализ и решение задачи 3

1. Вычисление узлового напряжения. Для схемы с двумя узлами напряжение между ними можно подсчитать по формуле

где Е_i – ЭДС i-й ветви, g_i = 1/R₁.– ее проводимость.

Подставляем числовые значения:

2. Расчет токов в ветвях

Токи определяем на основании закона Ома для ветви с источником: напряжение на зажимах источника равно его ЭДС минус падение напряжения на его внутреннем сопротивлении:

3. Проверка правильности решения задачи.

3.1. Проверка расчетов по первому закону Кирхгофа.

При решении задачи не использовался узел a. Запишем уравнение для этого узла (рис. 2.31):

I₂ + I₄ + I₃ = 0,24 + 0,36 –0,6 = 0.

3.2. Проверка расчетов по балансу мощностей.

Мощности элементов схемы с ЭДС:

P_ист = E₁I₁+ E₂I₂ + E₃I₃ = 60∙0,24 + 48∙0,36 + 6∙(− 0,6) = 28,06 Вт.

Мощности, расходуемые в резистивных элементах схемы:

P_потр.= R₁I₁² + R₂I₂² + r₀₃I₃² = 200∙0,24² + 100∙0,36² + 9,5∙0,6² = 27,9 Вт.

P_потр.≈ P_ист

Баланс мощностей практически сошелся, следовательно, задача решена верно.

4.  Режимы работы источников ЭДС в схеме.

По результатам расчета U_ab < E₁, U_ab < E₂, т.е. эти элементы схемы работают источниками; т.к. U_ab > E₃, ток в третьей ветви направлен против E₃ и принятого перед началом расчета направления I₃, т.е. этот элемент схемы работает в режиме потребления энергии .

2.9.4. Расчет цепей методом эквивалентного генератора

Задача 4. В схеме рис. 2.32 E₁ = 10 В, E₂ = 25 В, R₁ = 20 Ом, R₂ = 40 Ом, R₃ = 5 Ом, R₄ = 6,36 Ом. Определить ток в ветви с резистором R₄. Как экспериментально определить параметры эквивалентного генератора?


Рис. 2.32. Расчетная схема

Анализ и решение задачи 4

1. Заменим по отношению к ветви с резистором R₄ всю остальную схему эквивалентным генератором (активным двухполюсником) с ЭДС E_э и внутренним сопротивлением r_0э (рис. 2.33 а). ЭДС E_э определяется по результатам расчета режима холостого хода генератора как напряжение между точками «а» и «с» схемы рис. 2.32 при разомкнутой ветви с резистором R₄.

После размыкания ветви с R₄ получается схема с двумя узлами рис. 2.33 б. Узловое напряжение

Рис. 2.33. Преобразованные расчетные схемы
Ток в ветви с ЭДС E₃

I₃ = (E₃ − U_bd) / R₃ = (25 − 20) / 5 = 1 А.

Для расчета напряжения между точками «а» и «с» в схеме рис. 2.33 б примем потенциал точки «а» равным нулю, тогда

φ_a = 0; φ_b = φ_a + E₁ = 10 В; φ_c = φ_b + R₃I₃ = 15 В; E_г = φ_c − φ_a = 15 В.

2. Для расчета внутреннего сопротивления генератора в схеме рис. 2.33 б закорачиваются все ЭДС (рис. 2.33 в) и определяется сопротивление по отношению к точкам «а» и «с»:



r_оэ = 3,64 Ом.

3. Ток в ветви с резистором R₄ (схема рис. 2.33 а)

I₄ = E_э / (r_0э + R₄) = 20 / (3,64 + 6,36) = 2 А.

4. Экспериментальное определение параметров эквивалентного генератора.

Исходя из эквивалентности схем (рис. 2.32 и рис. 2.33 а), E_э и r_0э можно рассчитать по результатам двух опытов. Разомкнув ветвь с R₄, измеряем напряжение между точками «с» и «а» U_xx, равное ЭДС E_э, (опыт холостого хода). Для определения r_0э проводится (если это допустимо) опыт короткого замыкания: заданная ветвь замыкается накоротко и измеряется ток в ней (I_к). При этом r_0э = E_э / I_к.