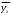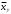КОНТРОЛЬНАЯ РАБОТА МАТЕМАТИКА. Задача в партии из 30 изделий 4 изделия имеют скрытый дефект. Какова вероятность того, что из взятых наугад 3 изделий 2 изделия являются дефектными
 Скачать 96.13 Kb. Скачать 96.13 Kb.
|
|
ЗАДАЧА 1. В партии из 30 изделий 4 изделия имеют скрытый дефект. Какова вероятность того, что из взятых наугад 3 изделий 2 изделия являются дефектными? ОТВЕТ: Количество всех исходов 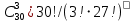 Количество благоприятных 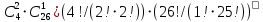 Тогда вероятность дефекта в условно отобранных деталях 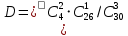 D = ((4!*26!)*(3!*27!))/(2!*2!*25!*30!)= = (2!*3*4*25!*26*2!*3*27!) / (2!*2!*25!*27!*28*29*30)=(3*4*26*3)/(28*29*30)= = 39/(29*35)=39/1015≈0,03842 ЗАДАЧА 2. На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: 20 с первого завода, 50 со второго, 30 с третьего. Вероятность качественного изготовления изделий на первом эаводе - 0,8, на втором - 0,9, на третьем - 0,8. Какова вероятность того, что взятое наугад изделие будет качественным? ОТВЕТ: 1) Общее количество деталей S=20+30+50=100. 2) Вероятность случайного выбора детали Dn каждого завода D1 =20/100=0.2 D2 =30/100=0.3 D3 =50/100=0.5 3) Вероятность выбора качественной детали соответственно Qn Q1 =0,8 Q2=0,9 Q3=0,8 3) Вероятность двух событий равна произведению вероятностей каждого из этих событий P1 = D1*Q1 = 0,2*0,8 = 0,16 P2 = D2*Q2 = 0,3*0,9 = 0,27 P3 = D3*Q3 = 0,5*0,8 = 0,4 И суммируем вероятности случайного выбора РS= 0,16+0,27+0,4 = 0,83 Вероятность того, что взятое наугад изделие будет качественным 0,83 или 83% ЗАДАЧА 3. Дано распределение дискретной случайной величины Х: 
Найти математическое ожидание и среднее квадратическое отклонение. ОТВЕТ: Математическое ожидание М(Х) = -3*0,3 + 2*0,4 + 3*0,2 +5*0,1 = 1 
Найдем дисперсию Д(Х) М(Х2) = 9*0,3 + 4*0,4 + 9*0,2 + 25*0,1 = 8,6 Д(Х)= М(Х2) - (М(Х)2= 8,6 – 1 = 7,6 Среднее квадратическое отклонение находится по формуле: (Х) 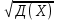 = 2,7568 = 2,7568Математическое ожидание 1. Среднее квадратическое отклонение 2,7568. ЗАДАЧА 4. В городе имеются 4 оптовые базы. Вероятность того, что товар требуемого вида отсутствует на этих базах, одинакова и равна 0,3. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент. ОТВЕТ: Х- число баз, на которых искомый товар отсутствует - может принимать значения : 0,1,2,3,4.n=4 –количество баз, p=0,3 –вероятность отсутствия товара на базе.По формуле Бернулли соответствующие вероятности будут таковы: 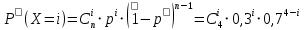  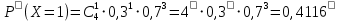 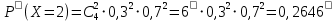 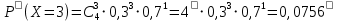 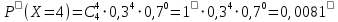 Так как данные события события несовместны и притом образуют полную группу событий, то сумма всех вероятностей равна единице. Закон распределения данной дискретной случайной величины составим в виде таблицы, где Xi - значения случайной величины. Pi- соответствующие вероятности.
ЗАДАЧА 5. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно 24, среднее квадратическое отклонение равно 1. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (20;26). ОТВЕТ: Для нормально распределённой случайной величины вероятность попадания случайной величины Х в интервал (α; β) находится по формуле : 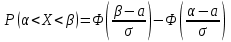 По условию известно 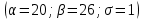 P( 20 < x < 26 )= Ф((26-24)/1) - Ф((20-24)/1)=Ф(2) - Ф(-4)= Ф(2)+Ф(4)= По таблице значений функции Лапласа=0,4772 +0,499968 =0,977368 
ЗАДАЧА 6. Найти выборочную среднюю и выборочную дисперсию по данному распределению выборки: ОТВЕТ: Выборочная средняя: n=ni=13+24+14+9=60 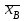 = = 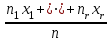 = =  = =  =14,8 =14,8Выборочная дисперсия: ДВ = 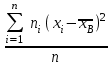 = = 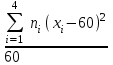 = = = 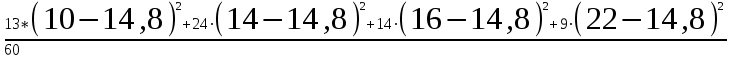 =13,36 =13,36. ЗАДАЧА 7. Найти выборочное уравнение линейной регрессии Y на Х на основании корреляционной таблицы:
Сравнить условные средние, вычисленные: а) по полученному уравнению регрессии; б) по данным корреляционной таблицы при Х=25. При уровне значимости 0.05 проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе 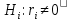 Для х1=5 распределение Y имеет вид
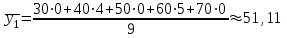 Значения вариантов Y, имеющие нулевые частоты в частных распределениях, записывать не будем 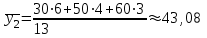   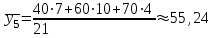  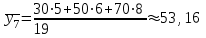 Распределение условных средних варианты Y выразится следующей таблицей:
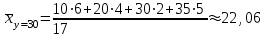 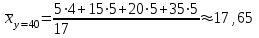 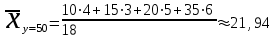   Распределение условных средних варианты Х:
Параметры а1 и а2 линейной зависимости 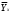 = а1х+а2 определяем из = а1х+а2 определяем из решения системы. В нашем случае имеем следующее:
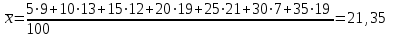 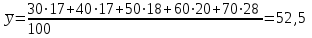  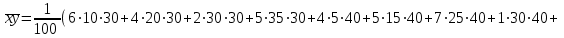 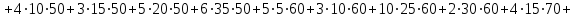  Получаем систему 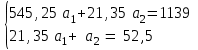 Отсюда а10,203, а2 = 48,16595 Отсюда а10,203, а2 = 48,16595Таким образом, искомое уравнение регрессии Y на Х запишется так: А) 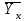 = 0,203х + 48,16595 = 0,203х + 48,16595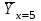 = 0,2035 + 48,16595 = 49,18095 = 0,2035 + 48,16595 = 49,18095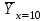 = 0,20310 + 48,16595 = 50,19595 = 0,20310 + 48,16595 = 50,19595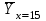 = 0,20315 + 48,16595 = 51,21095 = 0,20315 + 48,16595 = 51,21095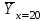 = 0,20320 + 48,16595 = 52,22595 = 0,20320 + 48,16595 = 52,22595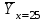 = 0,20325 + 48,16595 = 53,24095 = 0,20325 + 48,16595 = 53,24095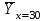 = 0,20330 + 48,16595 = 54,25595 = 0,20330 + 48,16595 = 54,25595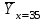 = 0,20335 + 48,16595 = 55,27095 = 0,20335 + 48,16595 = 55,27095В) 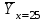 = 0,20325 + 48,16595 = 53,24095 = 0,20325 + 48,16595 = 53,24095 по данным таблицы при X=25 55,24 значение близко к табличному. С) Коэффициент корреляции определяется равенством rxy = 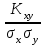 . . 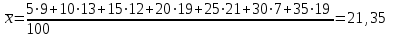  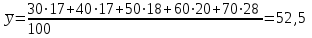  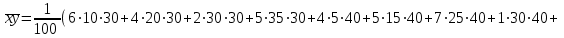 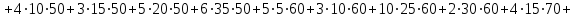  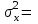 545,25 – (21,35)2 = 89,4275 545,25 – (21,35)2 = 89,4275 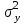 = 2967 – (52,5)2 = 210,65 = 2967 – (52,5)2 = 210,65Вычислим коэффициенты регрессий Y на Х и X на Y 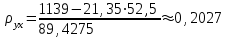 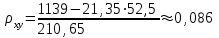 составим уравнения регрессий: 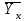 - 52,5 = 0,2027 (х – 21,35) - 52,5 = 0,2027 (х – 21,35)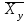 - 21,35 = 0,086 (y – 52,5) - 21,35 = 0,086 (y – 52,5)Окончательно 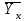 =0,2027 х + 48,172355; =0,2027 х + 48,172355; 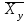 =0,086 y +16,835 =0,086 y +16,835Линейный выборочный коэффициент корреляции будет равен 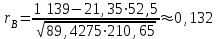 Таким образом, rВ 0,132 не равен нулю. |