прикладная механика. 26 вариант. Задача Вариант 10(64)

Название	Задача Вариант 10(64)
Анкор	прикладная механика
Дата	16.06.2022
Размер	0.51 Mb.
Формат файла
Имя файла	26 вариант.docx
Тип	Задача #595433
страница	1 из 3

1 2 3

Задача 1. Вариант -10(6+4).

Схема №4 Данные – строка - 10.

Стержень находится под действием сил.

Построить эпюры продольных сил и нормальных напряжений по длине бруса, а также эпюру перемещений поперечных сечений бруса. Материал – аллюминий. Принять для аллюминия:

Таблица 1. Исходные данные к задаче 1.

_{№ схемы}	_{Линейные размеры, м}			_F_{, кН}	_{Материал}	_{Площадь, см2}
_{№ схемы}	_а	_b	_c	_F_{, кН}	_{Материал}	_А
₄	₅	₆	₆	₁₇	_{Аллюминий}	₁₅

_{Решение.}

₁Подробный ход решения - расчет стержня на растяжение-сжатие

Определим продольные силы на участках стержня, начиная с правого

N₁ = - 68 = -68кН

N₂ = - 68 = -68кН

N₃ = - 68 + 119 = 51кН

Напряжения равны продольной силе, деленной на площадь

σ₁ = -68000/1500=-45.33 МПа

σ₂ = -68000/4500=-15.11 МПа

σ₃ = 51000/4500=11.33 МПа

Удлинения участков определяем по закону Гука, учитывая продольную силу N, кН, длину l, м, площадь А, мм² и модуль упругости материала E, МПа

Δl = N×l/E×A

Δl₁ = -68000 × 6 / (69000 × 1500) = -0.003942м

Δl₂ = -68000 × 6 / (69000 × 4500) = -0.001314м

Δl₃ = 51000 × 5 / (69000 × 4500) = 0.000821м

Удлинение всего стержня равно сумме удлинений его участков

Δl = - 0.003942 - 0.001314 + 0.000821 = -0.00444 м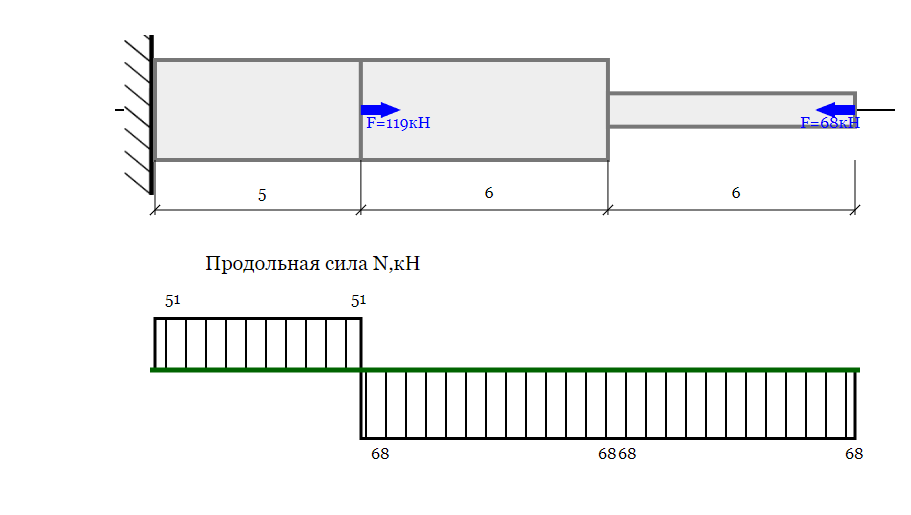

Задача №2. Схема №4. Данные – строка -10

.

Для стального вала постоянного поперечного сечения требуется:

1.Определить значения моментов М₁, М₂, М₃, М₄.

2.Построить эпюру крутящего момента.

3.Определить диаметр вала из расчётов на прочность.

4.Найти наибольший относительный угол закручивания.

5.Построить эпюру углов закручивания для вала.

При расчёте использовать следующие данные:

Таблица 2. Исходные данные к задаче 2.

М₁, кНм	М₂, кНм	М₃, кНм	М₄, кНм	_{а, м}	_b_{, м}	_c_{, м}	, МПа	_{Материал}
10	1	2	3	1,2	1,3	1,4	80	Серый чугун

Решение.

Реакции опор

Сумма моментов всех сил относительно точки A должна равняться нулю:
∑M^A = - M_A - ∑q_i(b_i - a_i)(a_i + b_i)/2 - ∑F_ic_i - ∑M_i =
= - M_A - M₁ - M₂ - M₃ - M₄ = - M_A - 10 + 1 - 2 - 3 =
= - M_A - 14 = 0 ⇒
⇒ M_A = -14 кНм;

Сумма проекций всех сил на вертикальную ось должна равняться нулю:
∑Y = R_A - ∑q_i(b_i - a_i) - ∑F_i =
= R_A = R_A =
= R_A + 0 = 0 ⇒
⇒ R_A = 0;

Для проверки вычислим сумму моментов всех сил относительно точки B:
∑M^B = - M_A - R_A L + ∑q_i(b_i - a_i)(2L - a_i - b_i)/2 + ∑F_i(L - c_i) - ∑M_i =
= - M_A - R_A L - M₁ - M₂ - M₃ - M₄ = 14 + 0·6.1 - 10 + 1 - 2 - 3 =
= 14 + 0 - 10 + 1 - 2 - 3 = 0;

Начальные параметры

Прогиб и поворот в заделке равны нулю: w₀ = 0; θ₀ = 0.

Построение эпюр

Составим аналитические выражения Q(z), M(z), EIθ(z) и EIw(z) для каждого участка и вычислим их значения в характерных точках.

Участок I (0 ≤ z ≤ 1.2)

Изгибающий момент M:
M_I(z) = M_A + R_A z = -14 + 0z =
= -14;

Значения M на краях отрезка:
M_I(0) = -14 кНм;
M_I(1.2) = -14 кНм;

Угол поворота сечения θ:
EIθ_I(z) = M_A z + R_A z²/2 = -14z + 0z²/2 =
= -14z;

Значения EIθ на краях отрезка:
EIθ_I(0) = -14·0 = 0;
EIθ_I(1.2) = -14·1.2 = -16.8 кНм²;

Прогиб w:
EIw_I(z) = M_A z²/2 + R_A z³/6 = -14z²/2 + 0z³/6 =
= - 7z²;

Значения EIw на краях отрезка:
EIw_I(0) = - 7·0² = 0;
EIw_I(1.2) = - 7·1.2² = -10.08 кНм³;

Участок II (1.2 ≤ z ≤ 2.5):

Изгибающий момент M:
M_II(z) = M_A + R_A z + M₁ = -14 + 0z + 10 =
= -4;

Значения M на краях отрезка:
M_II(1.2) = -4 кНм;
M_II(2.5) = -4 кНм;

Угол поворота сечения θ:
EIθ_II(z) = M_A z + R_A z²/2 + M₁(z - d₁) = -14z + 0z²/2 + 10(z - 1.2) =
= -4z - 12;

Значения EIθ на краях отрезка:
EIθ_II(1.2) = -4·1.2 - 12 = -16.8 кНм²;
EIθ_II(2.5) = -4·2.5 - 12 = -22 кНм²;

Прогиб w:
EIw_II(z) = M_A z²/2 + R_A z³/6 + M₁(z - d₁)²/2 = -14z²/2 + 0z³/6 + 10(z - 1.2)²/2 = -14z²/2 + 0z³ + 10(z²/2 - 1.2z + 0.72) =
= - 2z² - 12z + 7.2;

Значения EIw на краях отрезка:
EIw_II(1.2) = - 2·1.2² - 12·1.2 + 7.2 = -10.08 кНм³;
EIw_II(2.5) = - 2·2.5² - 12·2.5 + 7.2 = -35.3 кНм³;

Участок III (2.5 ≤ z ≤ 3.9):

Изгибающий момент M:
M_III(z) = M_A + R_A z + M₁ + M₂ = -14 + 0z + 10 - 1 =
= -5;

Значения M на краях отрезка:
M_III(2.5) = -5 кНм;
M_III(3.9) = -5 кНм;

Угол поворота сечения θ:
EIθ_III(z) = M_A z + R_A z²/2 + M₁(z - d₁) + M₂(z - d₂) = -14z + 0z²/2 + 10(z - 1.2) - 1(z - 2.5) =
= -5z - 9.5;

Значения EIθ на краях отрезка:
EIθ_III(2.5) = -5·2.5 - 9.5 = -22 кНм²;
EIθ_III(3.9) = -5·3.9 - 9.5 = -29 кНм²;

Прогиб w:
EIw_III(z) = M_A z²/2 + R_A z³/6 + M₁(z - d₁)²/2 + M₂(z - d₂)²/2 = -14z²/2 + 0z³/6 + 10(z - 1.2)²/2 - 1(z - 2.5)²/2 = -14z²/2 + 0z³ + 10(z²/2 - 1.2z + 0.72) - 1(z²/2 - 2.5z + 3.125) =
= - 2.5z² - 9.5z + 4.075;

Значения EIw на краях отрезка:
EIw_III(2.5) = - 2.5·2.5² - 9.5·2.5 + 4.075 = -35.3 кНм³;
EIw_III(3.9) = - 2.5·3.9² - 9.5·3.9 + 4.075 = -71 кНм³;

Участок IV (3.9 ≤ z ≤ 6.1):

Изгибающий момент M:
M_IV(z) = M_A + R_A z + M₁ + M₂ + M₃ = -14 + 0z + 10 - 1 + 2 =
= -3;

Значения M на краях отрезка:
M_IV(3.9) = -3 кНм;
M_IV(6.1) = -3 кНм;

Угол поворота сечения θ:
EIθ_IV(z) = M_A z + R_A z²/2 + M₁(z - d₁) + M₂(z - d₂) + M₃(z - d₃) = -14z + 0z²/2 + 10(z - 1.2) - 1(z - 2.5) + 2(z - 3.9) =
= -3z - 17.3;

Значения EIθ на краях отрезка:
EIθ_IV(3.9) = -3·3.9 - 17.3 = -29 кНм²;
EIθ_IV(6.1) = -3·6.1 - 17.3 = -35.6 кНм²;

Прогиб w:
EIw_IV(z) = M_A z²/2 + R_A z³/6 + M₁(z - d₁)²/2 + M₂(z - d₂)²/2 + M₃(z - d₃)²/2 = -14z²/2 + 0z³/6 + 10(z - 1.2)²/2 - 1(z - 2.5)²/2 + 2(z - 3.9)²/2 = -14z²/2 + 0z³ + 10(z²/2 - 1.2z + 0.72) - 1(z²/2 - 2.5z + 3.125) + 2(z²/2 - 3.9z + 7.605) =
= - 1.5z² - 17.3z + 19.285;

Значения EIw на краях отрезка:
EIw_IV(3.9) = - 1.5·3.9² - 17.3·3.9 + 19.285 = -71 кНм³;
EIw_IV(6.1) = - 1.5·6.1² - 17.3·6.1 + 19.285 = -142.06 кНм³;

Деформация кручения.
Задача 3. Схема №64 Данные – строка – 10.

.

Для заданной стальной балки, определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Из условия прочности рассчитать размеры поперечного сечения балки. Рассмотреть два варианта: а)поперечное сечение в виде круга диаметром «d».

б) двутавровое сечение.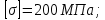

_{Исходные данные к задаче 3.}

F,кН	q, кН/м	M, кНм		_{а, м}	_b_,_м	_{с, м}
120	2	11	200	1,4	1,0	2,8

Рис.1 — Расчетная схема балки

Рис.1 — Расчетная схема балки
Определение опорных реакций

1) Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.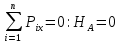

Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке A:

Найдем сумму моментов относительно шарнирно-подвижной опоры в точке B:

2) Вычислим реакцию шарнирно-подвижной опоры в точке B: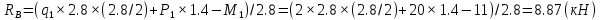

Так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону.

3) Вычислим реакцию шарнирно-неподвижной опоры в точке A:

Так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону.

4) Решаем полученную систему уравнений, находим неизвестные:

5) Выполним проверку решения, подставляя найденные значения в уравнение равновесия относительно оси Oy:

1 2 3

прикладная механика. 26 вариант. Задача Вариант 10(64)

1Подробный ход решения - расчет стержня на растяжение-сжатие

₁Подробный ход решения - расчет стержня на растяжение-сжатие