Математика. Трапеция. Задача Возле дома посадили 2 вишни и 3 березы. Сколько деревьев стало расти возле дома

• Название: Задача Возле дома посадили 2 вишни и 3 березы. Сколько деревьев стало расти возле дома
• Анкор: Математика
• Дата: 17.03.2023
• Размер: 242.29 Kb.
• Имя файла: Трапеция.docx
• Тип: Документы; #998143

Вопрос 1

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Укажите примеры сплошного обследования (3 примера):

Выберите один или несколько ответов:

a. регистрация заболевших опасным вирусом 

b. регистрация новорожденных 

c. регистрация вступивших в брак 

d. регистрация стипендии студентов, для подсчета размера средней стипендии по стране

Вопрос 2

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Прямые параллельные, если:

Выберите один ответ:

a. накрест лежащие углы равны 

b. сумма накрест лежащих углов равна 90 градусов

c. сумма накрест лежащих углов равна 180 градусов

d. накрест лежащие углы любые

Вопрос 3

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Боковая сторона равнобедренной трапеции равна 5 см. Вторая боковая сторона равна:

Выберите один ответ:

a. 5 см 

b. может быть любой

c. 10 см

d. нельзя определить

Вопрос 4

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Задача: «Возле дома посадили 2 вишни и 3 березы. Сколько деревьев стало расти возле дома?» - является:

Выберите один ответ:

a. недоопределенной 

b. определенной

c. общего вида

d. переопределенной

Вопрос 5

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 352:

Выберите один ответ:

a. отсутствует в восьмеричной

b. существует во всех названных системах счисления

c. отсутствует в двоичной системе счисления 

d. отсутствует в 16-ной системе

Вопрос 6

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Степень разброса в серии результатов, дающая определенное понятие об изменчивости этих результатов -

Выберите один ответ:

a. дисперсия 

b. коэффициент вариации

c. средняя арифметическая

d. размах

Вопрос 7

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Отношение частоты варианта к объему выборки называется

Выберите один ответ:

a. варьированием

b. объемом выборки

c. вариантом выборки

d. относительной частотой 

Вопрос 8

Неверно

Баллов: 0,00 из 1,00

Отметить вопрос

Текст вопроса

Средняя линия треугольника равна 10 см. Одна из сторон треугольника равна:

Выберите один ответ:

a. 10 см

b. 5 см 

c. 20 см

d. 15 см

Вопрос 9

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Оператор задачи – это:

Выберите один ответ:

a. что необходимо найти в задаче

b. совокупность действий, которые необходимо выполнить 

c. свойства объектов

d. множество рассмотренных объектов в задаче

Вопрос 10

Верно

Баллов: 1,00 из 1,00

Отметить вопрос

Текст вопроса

Сумму всех частот ряда называют:

Выберите один ответ:

a. относительной частотой

b. вариантом выборки

c. объемом выборки 

d. варьированием

Вопрос 11

Верно

Баллов: 5,00 из 5,00

Отметить вопрос

Текст вопроса

Чему равна сумма чисел в десятеричной системе счисления 44₈ и 59₁₆


Выберите один ответ:

a. 20

b. 121

c. 125 

d. 19

e. 18

Отзыв

Ваш ответ верный.

Вопрос 12

Верно

Баллов: 5,00 из 5,00

Отметить вопрос

Текст вопроса

Дано:  

I={воспитанники детского сада}

А={младшая группа}

В={подготовительная группа}

С={мальчики}

D={занимаются танцами}

Напишите для следующего предложения формулу:

«Девочки, кроме младшей группы, которые занимаются танцами»

Выберите один ответ:

a. В∩С∩D

b. С\А\D

c. ¯((С)\А)∪D

d. ¯((С)\А)∩D 

e. С∩А∩D

Отзыв

Ваш ответ верный.

Вопрос 13

Верно

Баллов: 10,00 из 10,00

Отметить вопрос

Текст вопроса

В треугольнике ABC, угол С равен 90 градусам, сторона AB=10 см, AС=6 см.

Установите соответствие между величинами и их значениями

0,8	Ответ 1
8	Ответ 2
0,6	Ответ 3
12	Ответ 4
24	Ответ 5

Отзыв

Ваш ответ верный.

Вопрос 14

Выполнен

Балл: 20,00

Отметить вопрос

Текст вопроса

Дайте развернутый ответ:

Трапеция
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).



Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.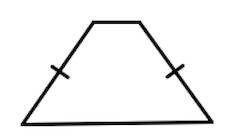



Трапеция,  у которой есть  прямые углы при боковой стороне, называется прямоугольной.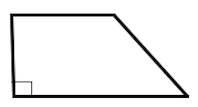



Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.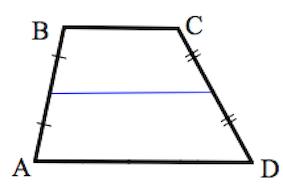



 

Свойства трапеции

 

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.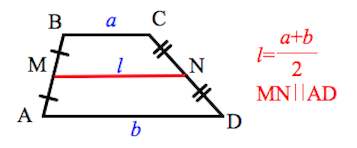



2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.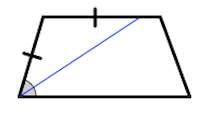



3. Треугольники  и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия – 

Отношение площадей этих треугольников есть .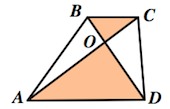



4. Треугольники  и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.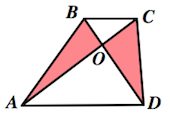



5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.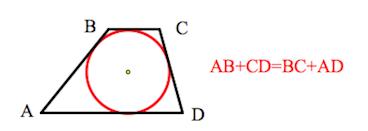



6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.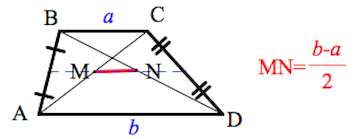



 

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.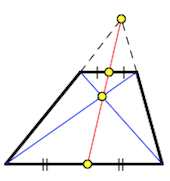



8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.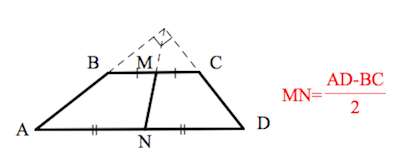



Свойства и признаки равнобедренной трапеции

 

1. В равнобедренной трапеции углы при любом основании равны.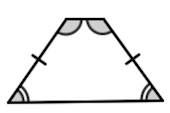



2. В равнобедренной трапеции длины диагоналей равны.

 

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.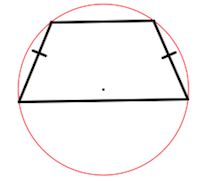



4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.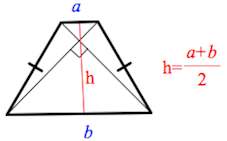



Вписанная  окружность

 

Если в трапецию вписана окружность с радиусом   и она делит боковую сторону точкой касания на два отрезка —  и ,  то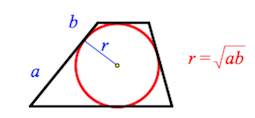 



 

Площадь

 

 или  где   – средняя линия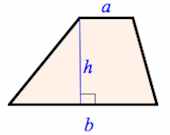