Галич_КР_1_В10_Заказ_5195814_24_03_23. Задача Заданы матрицы Вычислить определители матрицАиВи матрицу F. Решение. По формуле вычисляем определители матриц а и В
 Скачать 29.93 Kb. Скачать 29.93 Kb.
|
|
Контрольная работа 1. Линейная и векторная алгебра Задача 1. Заданы матрицы 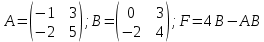 Вычислить определители матриц А и В и матрицу F. Решение. По формуле 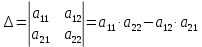 вычисляем определители матриц А и В: 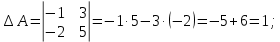 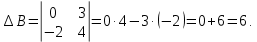 По формуле 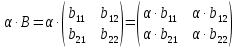 получаем: 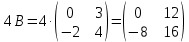 Произведение матриц А и В находим по формуле: 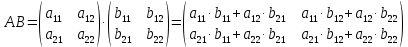 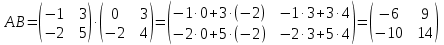 Матрицу F вычисляем с использованием формулы: 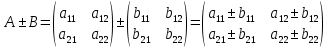 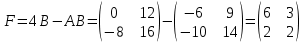 Задача 2. Даны системы линейных алгебраических уравнений. Требуется: а) решить систему по правилу Крамера; б) решить систему методом Гаусса. Сделать проверку полученных решений. 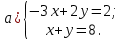 Решение. а) Решим систему по правила Крамера. Вычислим главный определитель системы: 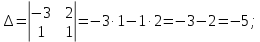 Главный определитель Δ = -5 ≠ 0, значит, по правилу Крамера система имеет единственное решение. Вспомогательные определители: 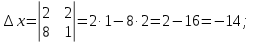 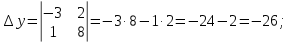 По формулам Крамера получаем: 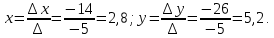 Проверка. Найденные значения неизвестных подставляем в уравнения системы: 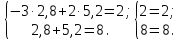 Система решена верно. Ответ: x = 2,8; y = 5,2. 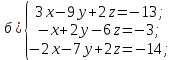 б) Решим систему методом Гаусса Расширенная матрица системы имеет вид: 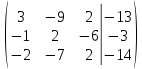 Делим каждую строку на ее первый элемент: 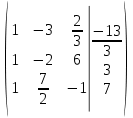 Из второй и третьей строк вычитаем первую строку: 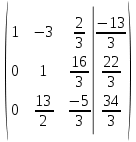 Вторую и третью строки делим на их первые элементы:  Из третьей строки вычитаем вторую 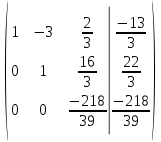 Третью строку делим на ее первый элемент: 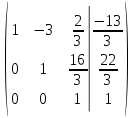 Полученной матрице соответствует преобразованная система: 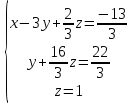 Из последнего уравнения системы получаем 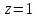 Из второго уравнения системы получаем: 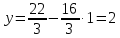 Из первого уравнения системы получаем: 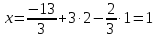 Проверка. Найденные значения неизвестных подставляем в уравнения системы: 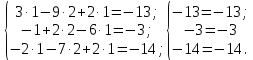 Система решена верно. Ответ: 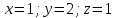 Задача 3. Заданы вершины треугольника АВС: А(5; 7; -1); В(-2; 4; 3); С(-6; 2; 2). Найти: а) векторы 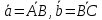 и их модули; б) угол и их модули; б) угол 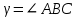 ; в) площадь треугольника АВС; г) высоту треугольника, опущенную из вершины С. ; в) площадь треугольника АВС; г) высоту треугольника, опущенную из вершины С.Решение. А) координаты векторов 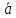 и и 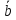 находим по формуле: находим по формуле: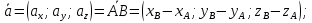 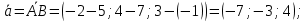 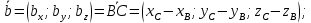 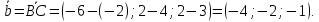 Модули векторов находим по формуле: 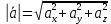 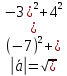 Б) Вычисляем скалярное произведение векторов по формуле: 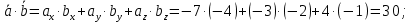 Найдем угол 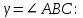 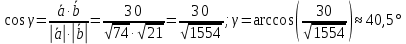 В) Вычисляем векторное произведение векторов по формуле: 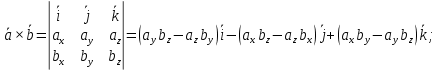 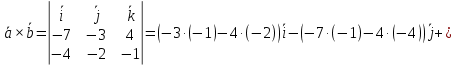 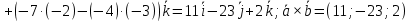 Площадь треугольника, построенного на векторах 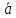 и и 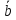 , равна половине модуля их векторного произведения, т.е. , равна половине модуля их векторного произведения, т.е.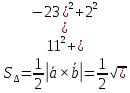 Г) Из формулы площади треугольника 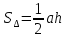 выразим высоту выразим высоту 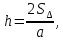 где где 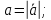 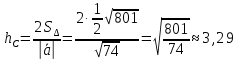 Задача 4. Заданы три вектора: 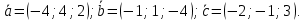 Требуется: а) выбрать пару перпендикулярных векторов (если такие есть); б) найти смешанное произведение векторов Требуется: а) выбрать пару перпендикулярных векторов (если такие есть); б) найти смешанное произведение векторов 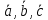 и объем параллелепипеда, построенного на векторах и объем параллелепипеда, построенного на векторах 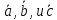 . .Решение. А) перпендикулярность векторов 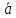 и и 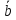 проверяют по условию: проверяют по условию: Вычислим скалярные произведения всех пар векторов: 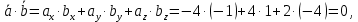 значит, векторы 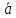 и и 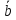 являются перпендикулярными; являются перпендикулярными;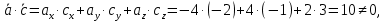 значит, векторы 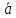 и и 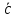 не являются перпендикулярными; не являются перпендикулярными;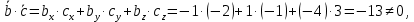 значит, векторы 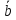 и и 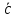 не являются перпендикулярными. не являются перпендикулярными.Б) находим смешанное произведение векторов 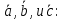 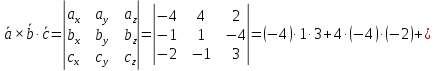 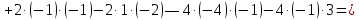 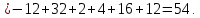 Объем параллелепипеда 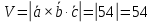 |
