основы мат.моделир. соц-цконом проц. (ЧАСТЬ 11). Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных
 Скачать 2.16 Mb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ (ЧАСТЬ 1/1) Группа Сд20ГУ171 Студент А.Г. Васильцева МОСКВА 2022 Практическое задание №1 1. Запишите вид парной линейной регрессии. Дайте определение всем входящим в нее элементам. В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель  где  - свободный член прямой парной линейной регрессии, - коэффициент направления прямой парной линейной регрессии, - случайная погрешность,N - число элементов генеральной совокупности. 2. В чем суть метода наименьших квадратов? Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 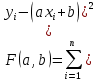 принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.3. Дайте интерпретацию параметров b1 и b0 линейной модели. Покажите их графическое представление. Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение парной регрессии достаточно распространенным в эконометрических исследованиях. Формально a – значение y при x = 0. Если x не имеет и не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать его могут привести к абсурду, особенно при a< 0. Интерпретировать можно лишь знак при параметре a. Если a> 0, то относительное изменение результата происходит медленнее, чем изменение фактора. 4. Что оценивает линейный коэффициент корреляции? Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). 5. Приведите примеры нелинейных моделей по объясняющей переменной x. Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: 1. полиномы разных степеней 2. равносторонняя гипербола 6. Что понимается под линеаризацией нелинейной модели? Сущность метода линеаризации заключается в том, что нелинейную функцию заменяют некоторой линейной и затем по уже известным правилам находят числовые характеристики этой линейной функции, считая их приближенно равными числовым характеристикам нелинейной функции. 7. Каким показателем характеризуется теснота связи факторов для нелинейной модели? Каковы свойства этого показателя? Мерой интенсивности связи при нелинейных соотношениях между переменными служит индекс корреляции. Индекс корреляции рассчитывается, когда выбрана конкретная нелинейная зависимость между переменными, построена эта зависимость и по ней определены теоретические значения результирующей переменной “ŷ”. 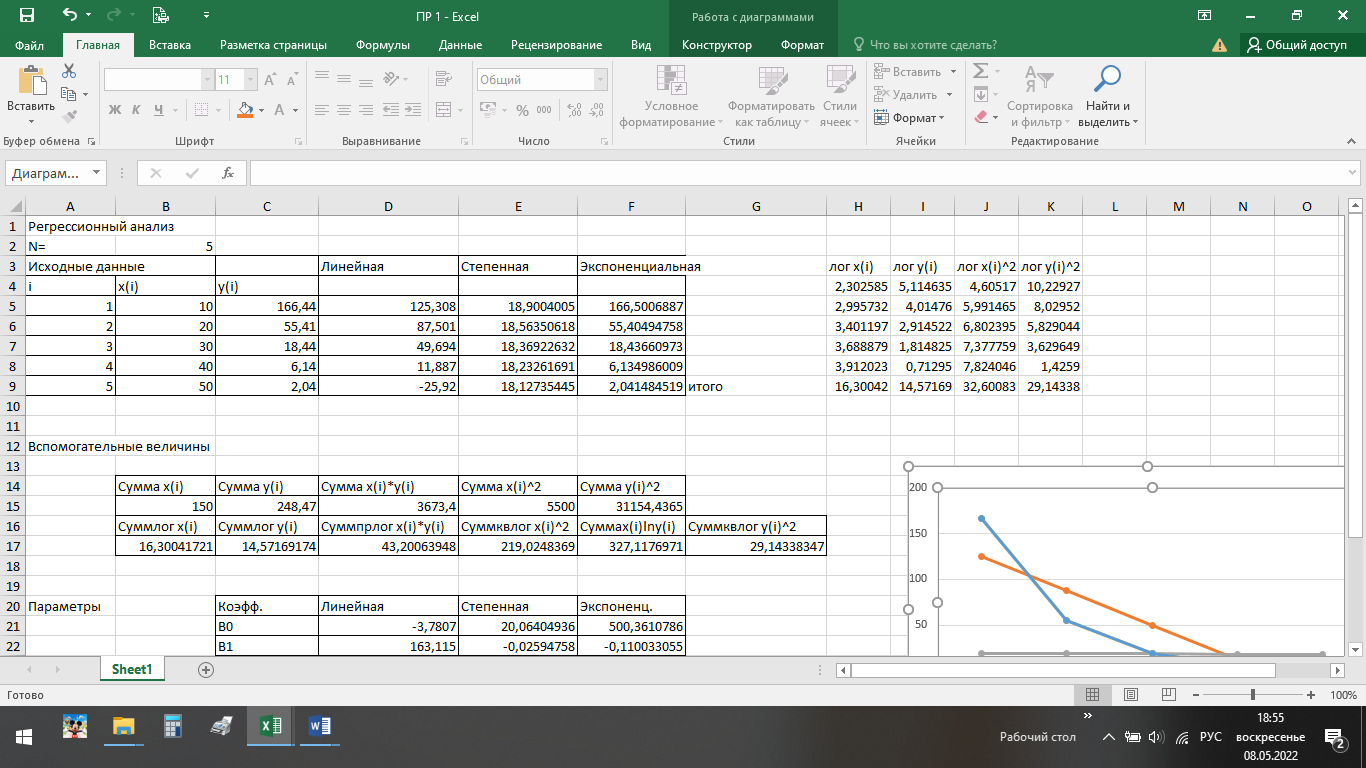 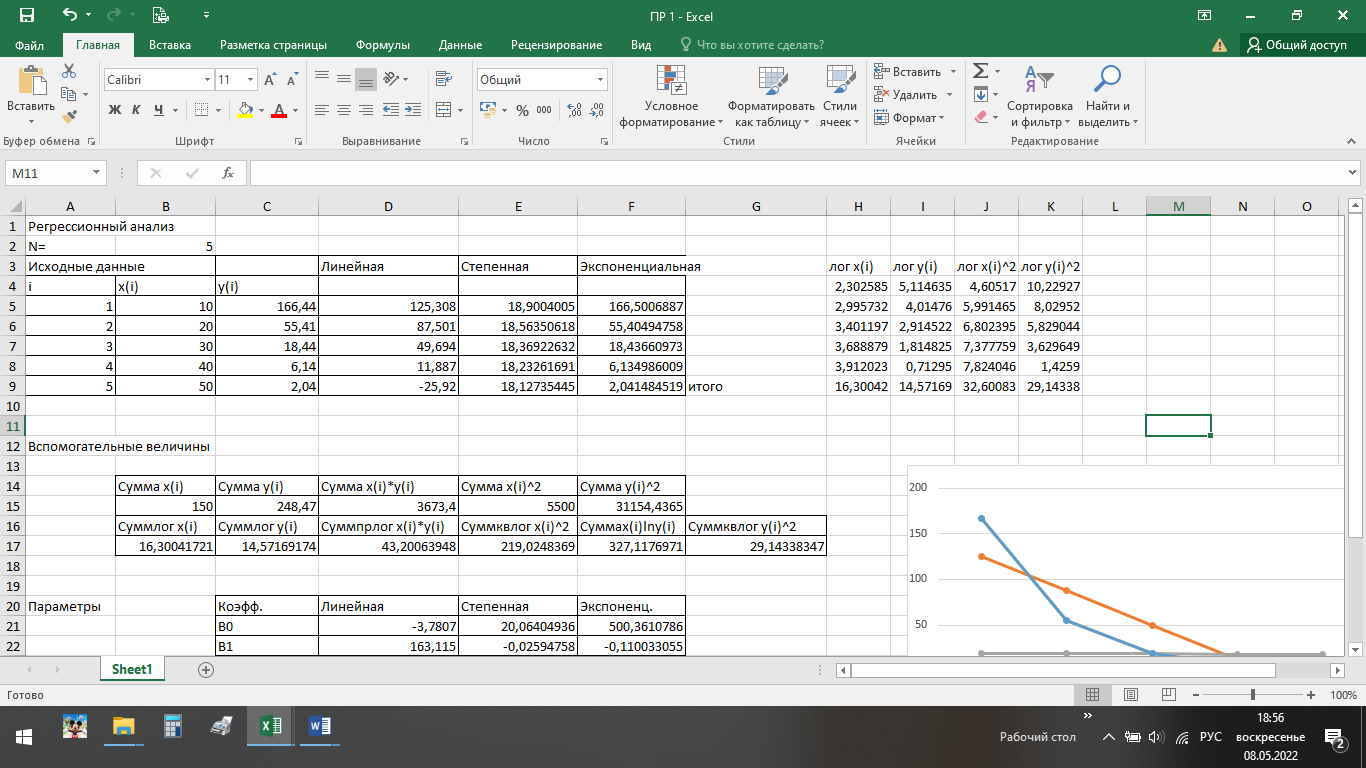 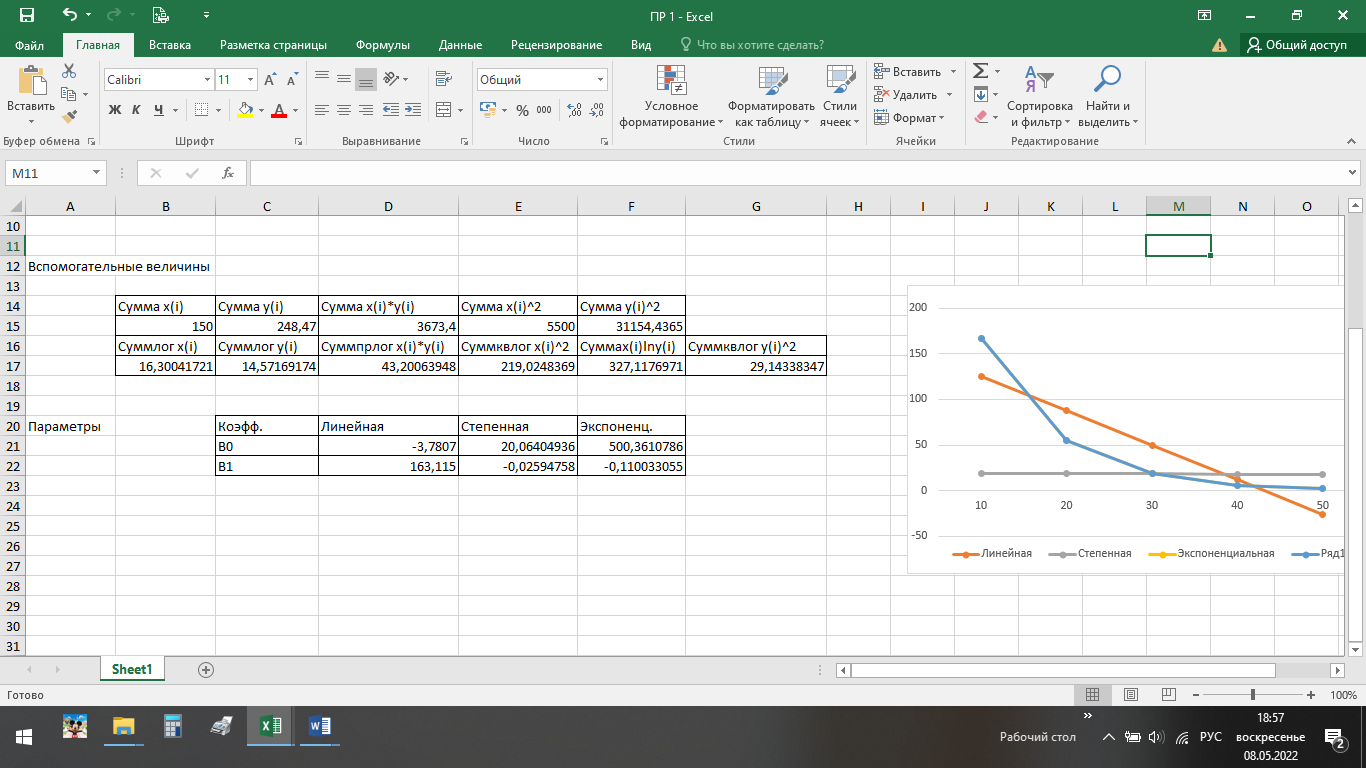 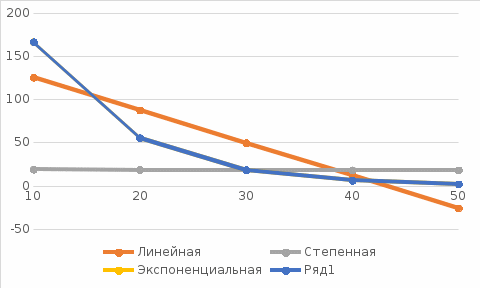 Практическое задание №2 Назовите основные методы решения ЗЛП. графический метод симплексный метод транспортная задача Поясните суть симплекс-метода решения ЗЛП. Симплекс метод - это метод последовательного перехода от одного базисного решения (вершины многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума). Поясните суть графического решения ЗЛП. Графический метод решения задач ЛП основан на их геометрической интерпретации и применяется для задач, имеющих две переменные. В случае трех переменных графическое решение задачи ЛП становится менее наглядным, а при большем числе переменных вообще невозможным. 5. Какие ресурсные ограничения используются в задачах ЗЛП? фонд машинного времени по каждому виду оборудования; фонд рабочего времени, определяемый численностью персонала; фонд материальных ресурсов, которые может получить в планируемый период предприятие от поставщиков по заключенным договорам. модели многих задач планирования базируются на законах сохранения (балансовых соотношениях) и эмпирических закономерностях преобразования ресурсов в продукцию (производственных функциях). Математически подобные модели представляются в виде систем m линейных уравнений с n неизвестными, которые решаются с помощью известных методов линейной алгебры (например, методом Гаусса). 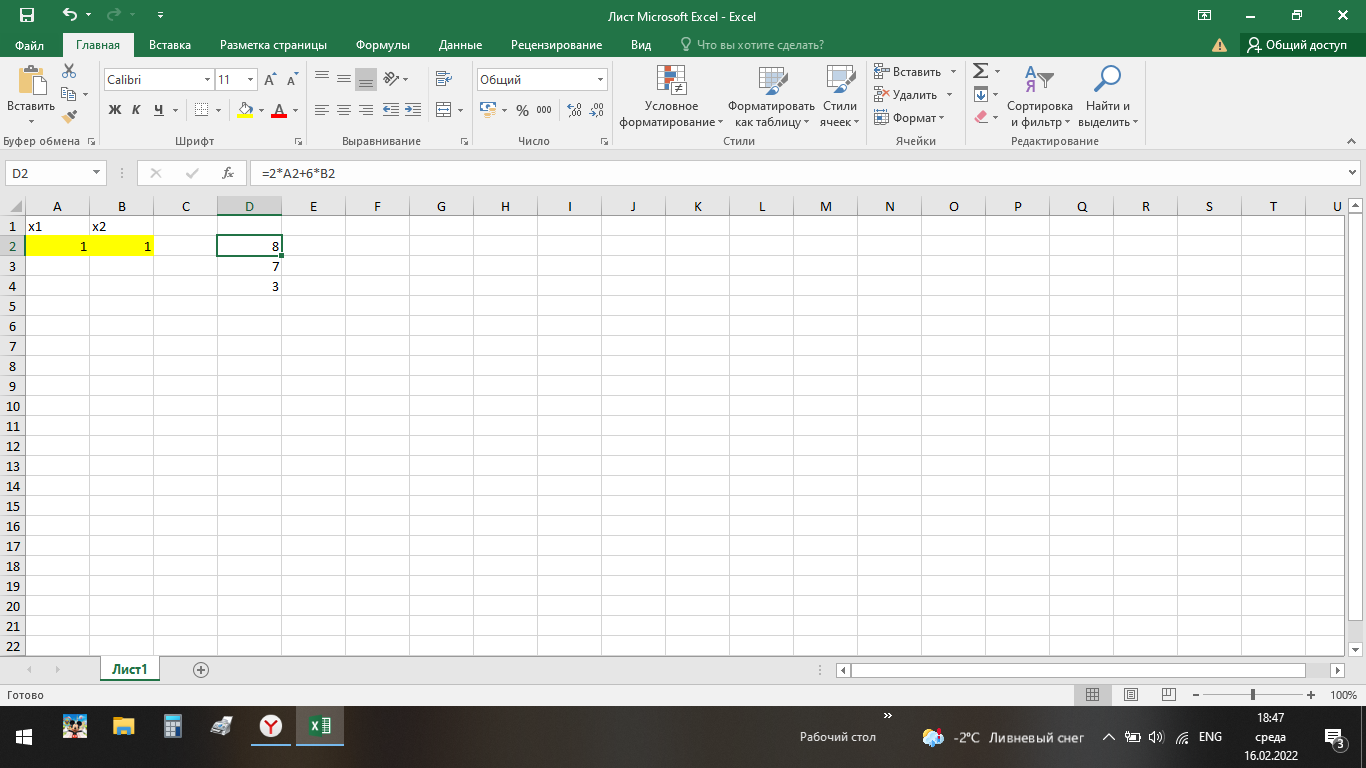 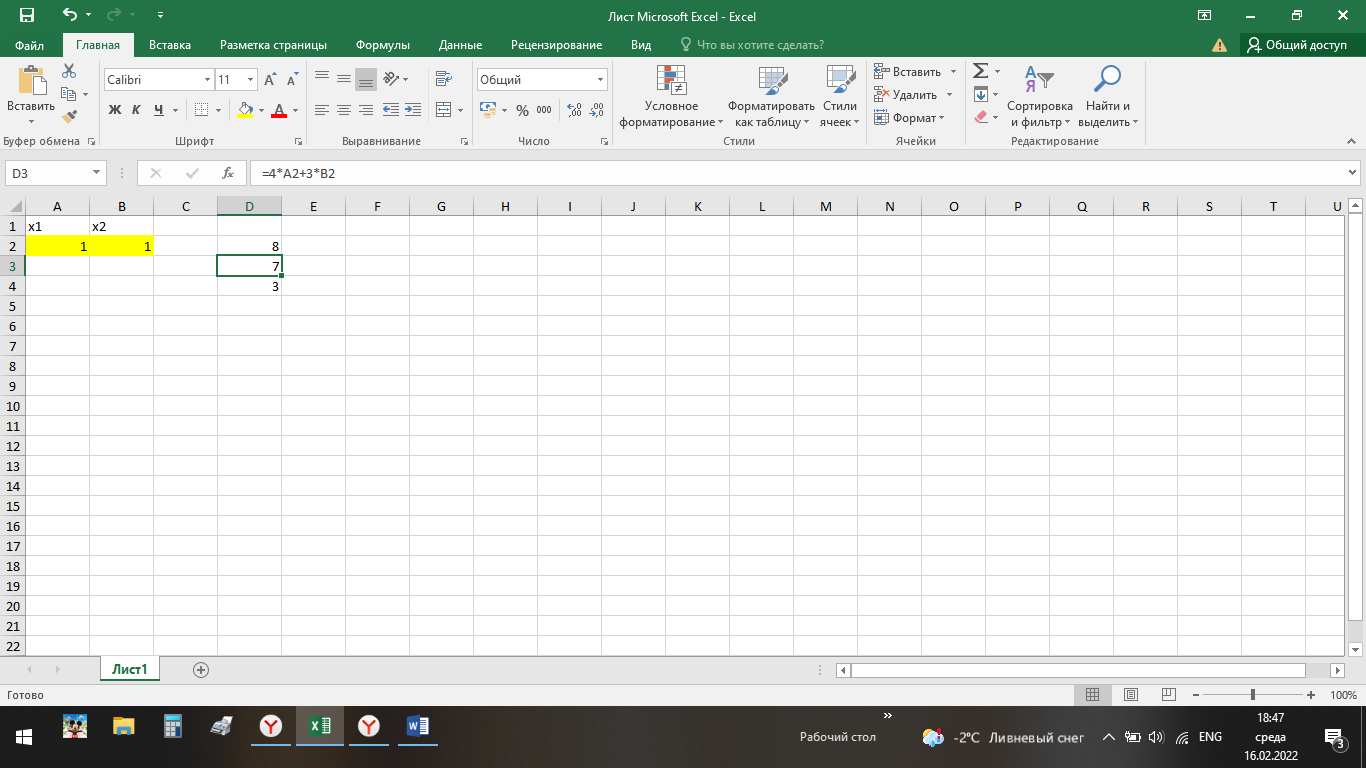 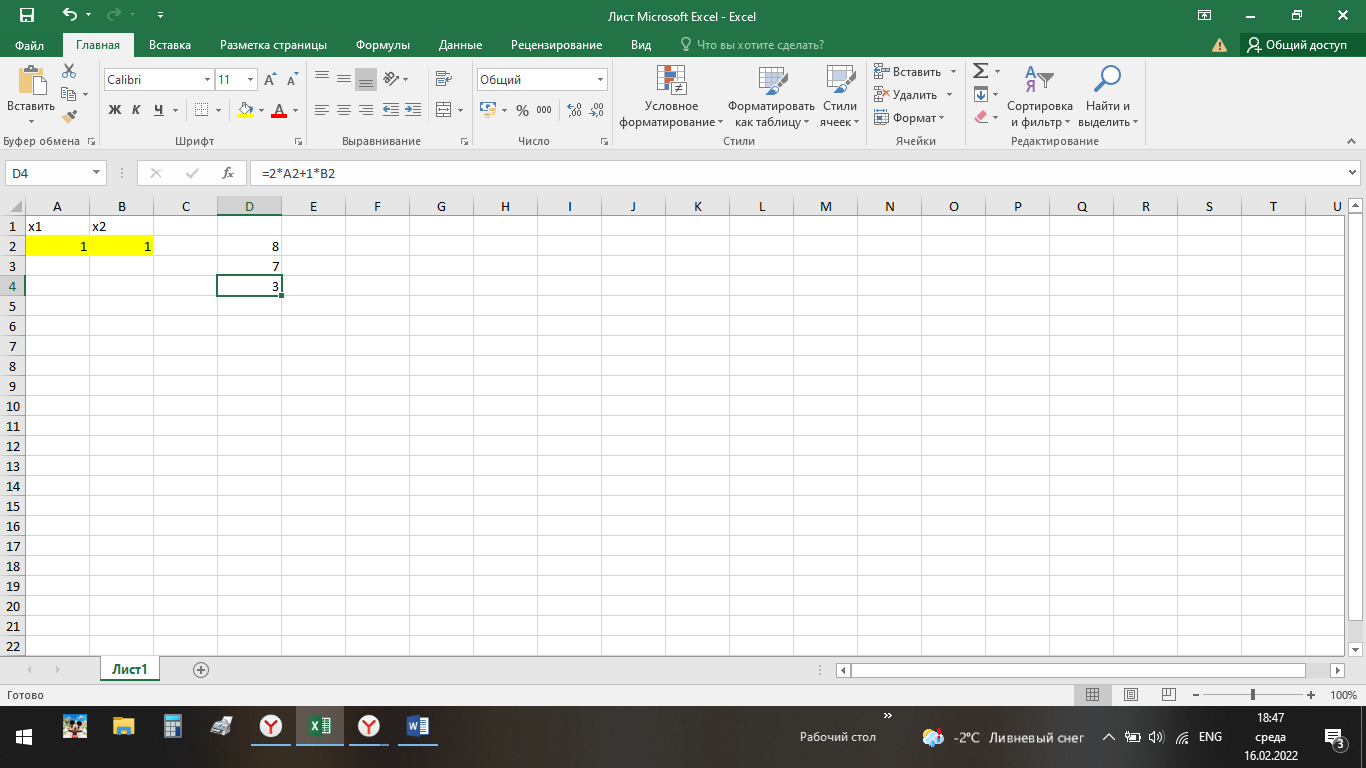  Практическое задание №3 Какие задачи линейного программирования называются транспортными? К ЗЛП транспортного типа (кратко: транспортной задаче− ТЗ) приходят при рассмотрении различных практических ситуаций, связанных с составлением наиболее экономичного плана перевозок продукции, управления запасами, назначением персонала на рабочие места, оборотом наличного капитала и многими другими. Каковы особенности математической модели транспортной задачи? Особенности экономико-математической модели транспортной задачи: • система ограничений есть система уравнений (т.е. транспортная задача задана в канонической форме); • коэффициенты при переменных системы ограничений равны единице или нулю; • каждая переменная входит в систему ограничений два раза. Какие транспортные задачи называются открытыми и закрытыми? Закрытая задача характеризуется тем, что суммарная потребность всех потребителей равна суммарным запасам всех складов. То есть, весь товар на всех складах будет реализован полностью. В открытой задаче суммарная потребность и суммарные запасы не совпадают. Например, какой-то склад не реализуется товар полностью, появляются остатки продукции. В этом случае процесс решения транспортной задачи немного усложняется, потребуется ввести фиктивного поставщика или потребителя с нулевыми стоимостями перевозки. Могут ли объемы перевозок быть отрицательными? Объемы перевозок не могут быть отрицательными    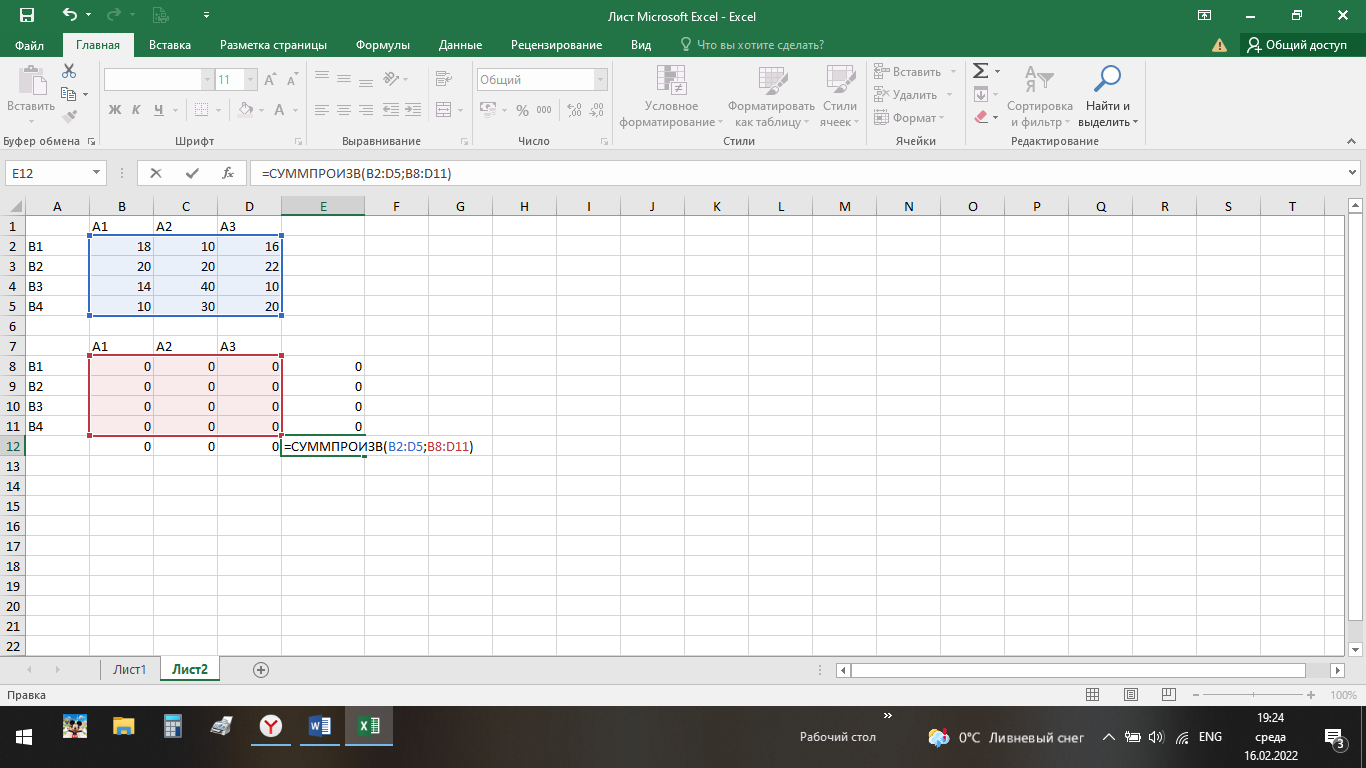 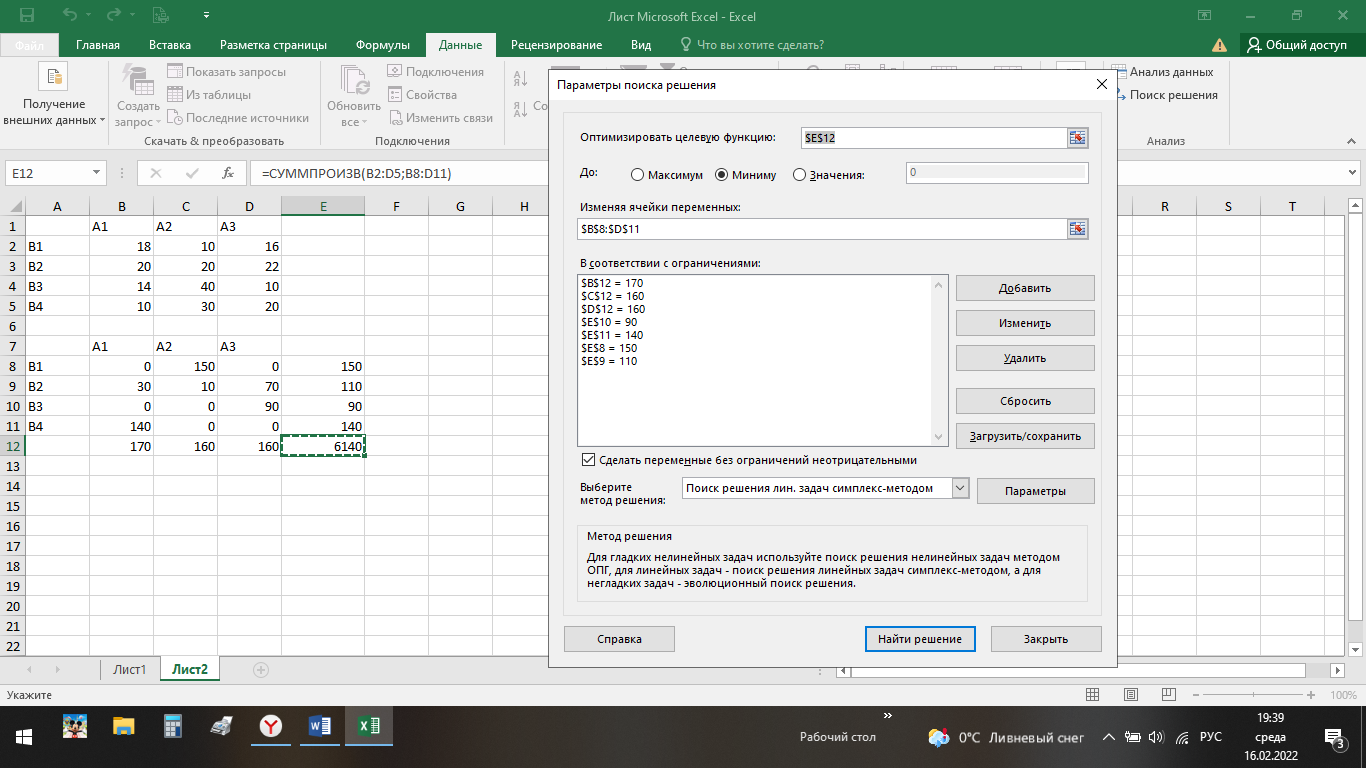 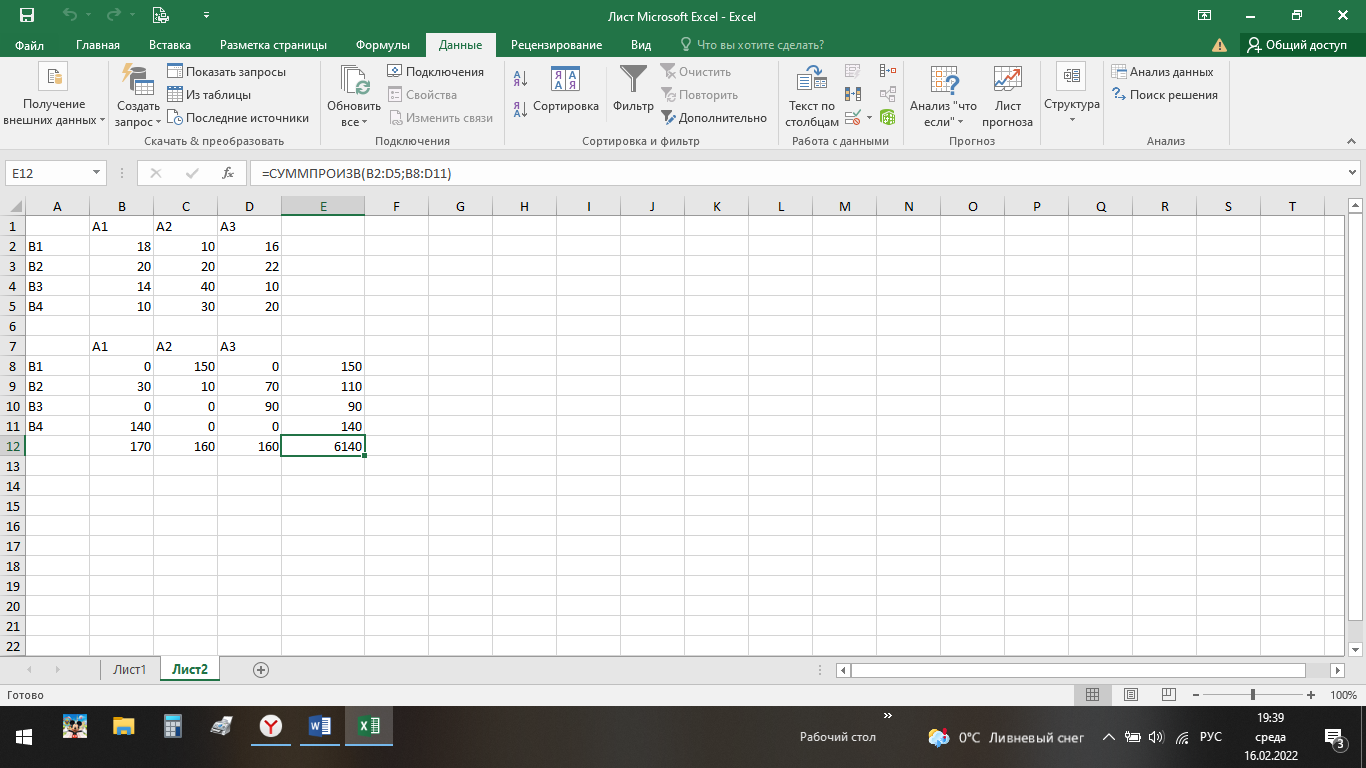 Практическое задание № 4 1. Объясните, в чем суть прогнозирования экономических процессов на основе метода динамических рядов? Суть экономико – математического метода прогнозирования экономических показателей заключается в построении математических моделей, которые отражают количественные взаимосвязи между показателями 2. Какие компоненты входят в состав динамического ряда? В состав динамического ряда входят: - тренд динамического ряда – регулярная компонента, характеризующая общую тенденцию; - сезонная компонента или внутригодичные колебания, а в общем случае – циклическая составляющая; - случайная компонента, образующаяся под влиянием различных неизвестных причин; - компонента, обеспечивающая сопоставимость элементов динамического ряда; - управляющая компонента, с помощью которой воздействуют на члены динамического ряда с целью формирования в будущем его желаемой траектории (управляемый прогноз). 3. Каким образом происходит расчет каждой из составляющих ряда? Компонента t Z может быть вычислена как 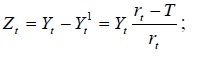 Вычисление регулярной компоненты t U (тренда) Известны несколько методов вычисления регулярной компоненты. К ним относятся: механические способы сглаживания, аналитические методы с применением определенных математических функций и, наконец, комбинированный способ. Вычисление сезонной t V и случайной t E компонент Для определения сезонной и случайной компонент вычисляется динамический ряд V * E * Y * U * Z , при t n =0. Нахождение случайной составляющей t E Временной ряд следует привести к сопоставимому виду, сезонную компоненту и тренд необходимо отфильтровать и вычесть из значений t Y , управление t n должно отсутствовать. 4. Как оценить адекватность трендовой модели? Трендовая модель  , конкретного временного ряда yt, считается адекватной, если правильно отражает систематические компоненты временного ряда. Это требование эквивалентно требованию, чтобы остаточная компонента  (t = 1, 2, ..., п) удовлетворяла свойствам случайной компоненты временного ряда, указанным в параграфе 4.1: случайность колебаний уровней остаточной последовательности, соответствие распределения случайной компоненты нормальному закону распределения, равенство математического ожидания случайной компоненты нулю, независимость значений уровней случайной компоненты.5. Почему рекомендуют автоматизировать работы по прогнозированию при разработке управленческих решений? Автоматизация позволяет сократить время и затраты на сбор информации и выполнение прогнозирования.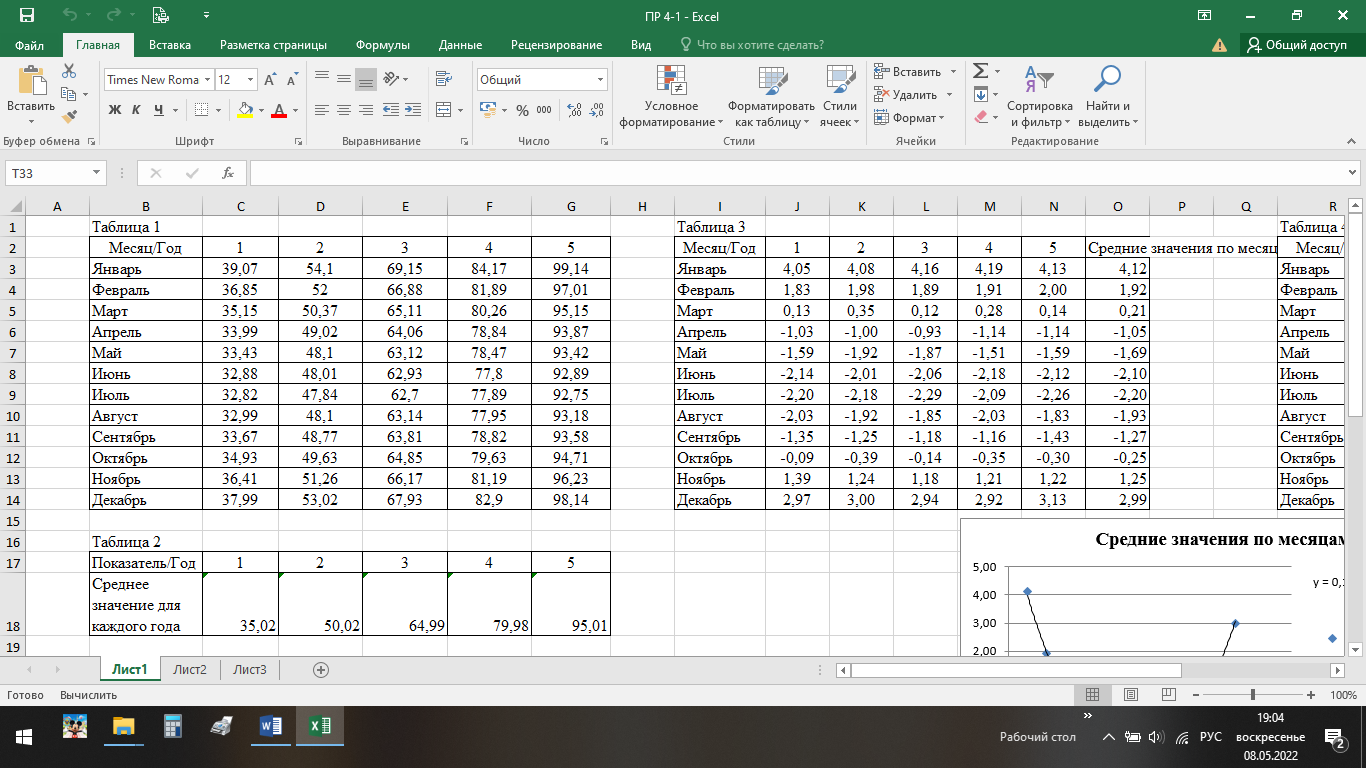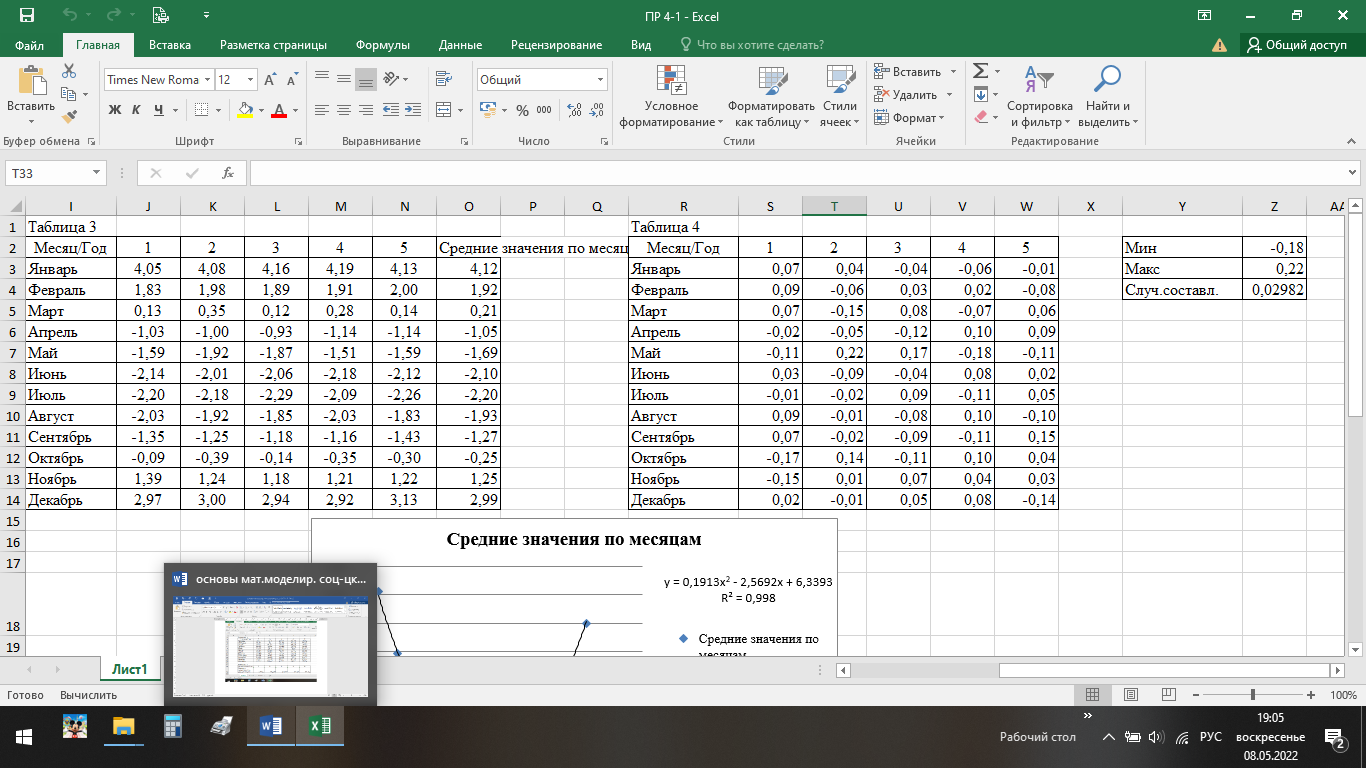   
Практическое задание № 5 1. Как рассчитать число серий эксперимента N? 2. Чем отличается линейная модель, нелинейная модель и линейная модель со смешанными оценками? Линейная и линейная модель со смешанными оценками требуют изменения факторов на двух уровнях, нелинейная модель – на трёх уровнях изменения факторов. Как оценить адекватность моделей? Модель считается адекватной, если ряд остатков обладает свойствами: независимость; их случайность; соответствие нормальному закону распределения; равенство нулю средней ошибки. 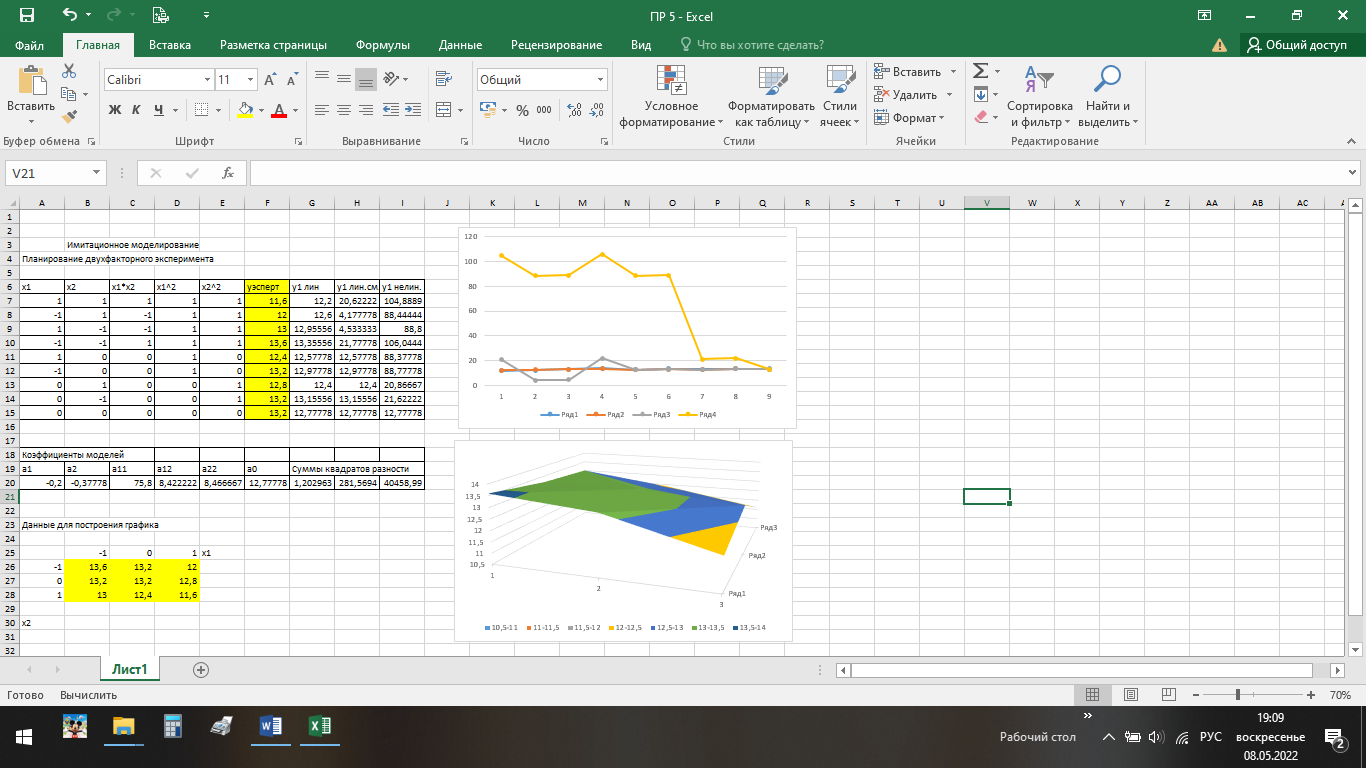 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||