задания. Задачи для контрольных

• Название: Задачи для контрольных
• Дата: 08.03.2023
• Размер: 99.72 Kb.
• Имя файла: задания.docx
• Тип: Документы; #974784

_Задачи для контрольных работ
вершины треугольника AВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр.
16. А(-2; 2), В(10; -7), С(8; 7).


даны координаты точек А, В, С. Требуется: 1) записать АВ и АС в системе орт и найти модули этих векторов; 2) найти угол между векторами АВи АС; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору АВ .

26. А(1; 0; -1), В(6; 1; -1), С(4; 5; 3).

даны векторы a₁ , a₂ , a₃ , b. Показать, что век-

торы

a₁ , a₂ , a₃

образуют базис трехмерного пространства и найти коорди

наты вектора bв этом базисе.

36. a₁ (1; 2; 5), a₂ (2; -3; 4),

a₃ (1; -1; -2), b (3; 0; 1).

систему уравнений записать в матричной фор ме и решить ее с помощью обратной матрицы






^{x 2 y 3z 1,} 46. _2x 3y z  7,



^4x y 2z 0.

найти указанные пределы (не пользуясь правилом Лопиталя).

^{ } .

x 1

56.a)

lim
3x²
 10 x  8 <sub>;

x</su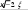b>2

б) lim

3x 1 ^;

x2 _{ 4}

в) lim ^x ;

arctg2 x

x

 2 x 1  ^3x

г) lim ^{ } .

2x 1

x0


x_{ }

найти производные функций.

76 . a) y

x³ ( 3 ln

x 1) 

x 1 <sub>;

e</sub>x

б) y

_{ ( 5} tg2 x

 3 ) ⁴ ;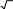

в) х³ у³ 

2 xy

 1  0 .

исследовать данные функции методами дифференци- ального исчисления и построить их графики. Исследование функции рекомен- дуется проводить по следующей схеме: 1) найти область определения функ- ции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы монотонности функции

и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.

6

95. 
    y
    

95. 
    y
    

.

x²  3

найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.

135. 
     a) _sin³ xcos xdx;
     

б) _

x³  2

2

dx;

в) _ arccos2xdx.

x 3x 2

вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.

156. y x²

 4x 4; у х.

вычислить объем тела, образованного вращени- ем вокруг оси Оу фигуры, ограниченной указанными линиями. Сделать

чертеж.

166. y²

 4  x;
x 0.

найти общее решение дифференциальных уравнений первого порядка.

176. y^ 

_ex y_.

найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям.

196. y^ 

9 y cos 3x,

y(0)  1,

y^ (0)  3.

дан степенной ряд. Найти интервал сходимости ряда и исследовать его сходимость на концах интервала.

n



205.

n1⁵  x²ⁿ_{. 206.} ^


_xn _.





n 1

2n1

n^ 1^{3 8n11}





n 1

_xn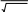

nn1 ^.

246. Вероятность попадания в цель при одном выстреле равна 0,7. Производится 4 выстрела. Найти вероятность того, что цель будет по- ражена: а) три раза; б) не более двух раз.

задан закон распределения дискретной слу- чайной величины Х (в первой строке указаны возможные значения ве- личины X, во второй строке даны вероятноcти р этих значений). Найти:

1. 
   математическое ожидание МХ; 2) дисперсию DX; 3) среднее квадра- тическое отклонение .
   

276. Х	15	11	13	12
р	0,2	0,5	0,2	0,1

случайная величина Х задана интегральной функцией распределения F(х). Найти: 1) дифференциальную функцию распределения f(х); 2) математическое ожидание МХ; 3) дисперсию DХ.

^{0 при}



х 0,

⁰



 _x3

при

х 0,

281. F( x) 

_x2

при

0  x 1,

286. F( x)  ^ при0 

8

x 2,


^1 при

х 1.



_1 при

х 2.

Библиографическийсписок

1. 
   Пискунов Н.С. Дифференциальное и интегральное исчисление. – М.: Наука, 1985. – Т. 1 – 432 с. – Т. 2 – 429 с.
   
2. 
   Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в уп- ражнениях и задачах. Ч.1,2. – М.: Высшая школа, 1986.
   
3. 
   Сборник задач по курсу высшей математики/Под ред. П.Е. Дюбюка и Г.М. Кручковича. – М.: Высшая школа, 1965. – 592 с.