аксаесесвкв. Задачи к устному экзамену. 10 класс
 Скачать 25.15 Kb.
|
|
Задачи к устному экзамену. 10 класс. Билет №1 1. В основании пирамиды лежит прямоугольный треугольник АВС, угол С - прямой, АВ=29 см, АС = 21 см, АД перпендикулярна плоскости АВС, АД = 20 см. Найдите площадь боковой поверхности пирамиды ДАВС. 2. Ребро куба АВСДА1В1С1Д1 равно 2 см. Найдите угол между прямыми АВ и А1С Билет №2 1.В правильной треугольной пирамиде сторона основания равна 6 см. Высота пирамиды равна 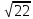 см. Найдите площадь боковой поверхности пирамиды.2. Ребро куба АВСДА1В1С1Д1 равно 2 см. Найдите угол между прямыми АВ1 и ВС1. Билет №3 1.В основании прямого параллелепипеда лежит ромб, площадь которого равна 60 см2 . Площади диагональных сечений 72 см2 и 60 см2 . Найдите высоту параллелепипеда. 2. Высота правильной четырехугольной пирамиды равна 6 см. Площадь боковой поверхности пирамиды равна 96 см2 . Найдите двугранный угол при основании пирамиды. Билет №4 1. Через вершину С равнобедренного треугольника АВС ( АС = ВС ) проведена прямая СМ, перпендикулярная к его плоскости. Найдите расстояние от точки М до прямой АВ, если АС = ВС = 7 см, АВ= 12 см, СМ= 2 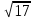 см.2. АВСДА1В1С1Д1 – прямоугольный параллелепипед. АВ =4, АД = 6, АА1 = 10. Найдите угол между прямой В1Д и плоскостью (ДСС1). Билет №5 1.Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно в точках А1 и А2 , а сторону АС этого угла соответственно в точках В1 и В2; А1В1 = 18 см, АА1 = 24 см, АА1: А1А2= 2:3. Найдите А2В2 . 2. Основанием тетраэдра ДАВС является правильный треугольник АВС со стороной 4 см. Грани ДВС и ДВА перпендикулярны плоскости основания, их общее ребро равно 2 см. Найдите угол, между плоскостями ДАС и АВС. Билет №6 1. В правильном тетраэдре ДАВС ребро 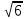 см. Найти расстояние от вершины А до плоскости ВДС.2. В основании прямого параллелепипеда лежит ромб, площадь которого равна 60 см2. Площади диагональных сечений 72 см2 и 60 см2 . Найдите высоту параллелепипеда. Билет №7 1. В основании пирамиды лежит равнобедренный треугольник АВС (АВ=АС). АВ=АС=15 см, ВС = 24 см. Все боковые грани наклонены к основанию под одним и тем же углом. Высота пирамиды 2 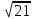 см. Найти апофему пирамиды.2. АВСДА1В1С1Д1 – прямая призма, в основании которой лежит квадрат со стороной 2 см. Боковое ребро призмы равно  см. Найдите угол между плоскостью АВ1С и плоскостью основания призмы.Билет №8 1. В правильном тетраэдре ДАВС точка Е - середина ребра СД. Найдите угол между прямыми ВС и АЕ. 2. Апофема правильной четырехугольной пирамиды равна  , а сторона основания равна 8. Найдите угол между основанием пирамиды и плоскостью сечения, проходящего через сторону основания и середину скрещивающегося с ним бокового ребра.Билет №9 1. В правильной четырехугольной пирамиде сторона основания равна 8 см. Высота пирамиды равна  см. Найдите площадь полной поверхности пирамиды.2. Ребро куба АВСДА1В1С1Д1 равно  см. Найдите расстояние от вершины С до плоскости ВДС1.Билет №10 1. В основании пирамиды лежит равнобедренный треугольник АВС (АВ=АС). ВС = 6 см, АК – высота основания, АК= 9 см. Боковые ребра пирамиды равны 13 см. Найти высоту пирамиды. 2. Высота правильной четырехугольной пирамиды равна 12 см, а боковое ребро 4 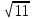 см. Найдите угол между основанием пирамиды и плоскостью сечения, проходящего через сторону основания и середину скрещивающегося с ним бокового ребра.Билет №11 1. Расстояние от точки М до плоскости α равно 12 см. Из точки М к плоскости α проведены две наклонные, длины которых равны 13 см и 15 см. Угол между проекциями наклонных равен 60о. Найти расстояние между основаниями наклонных. 2. Найдите отношение площади боковой поверхности правильной шестиугольной пирамиды к площади её основания, если сторона основания равна 1, а высота пирамиды 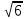.Билет №12 1. В основании пирамиды лежит параллелограмм со сторонами 10 см и 18 см, площадь которого равна 90 см2. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 6 см. Найти площадь боковой поверхности пирамиды. 2. В правильной четырехугольной пирамиде МАВСД, все ребра которой равны 1, Точка Е - середина ребра МД. Найдите угол между прямыми ВМ и АЕ. Билет №13 1.Основанием прямой призмы является треугольник со сторонами 4 см и 8 см, и углом между ними в 120о. Наибольшая из площадей боковых граней равна 12 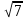 см2 . Найдите площадь боковой поверхности призмы.2.В правильной четырехугольной пирамиде МАВСД, все ребра которой равны 1, найдите угол, образованный плоскостями МВС и МСД. Билет №14 1. Основанием прямой призмы является параллелограмм со сторонами 4 см и 6 см и острым углом в 60о. Площадь меньшего диагонального сечения равна 10 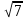см2. Найдите площадь боковой поверхности призмы.2. Высота правильной треугольной пирамиды равна 2 см, площадь боковой поверхности равна 72 см2. Найдите двугранный угол при основании пирамиды. Билет №15 1. Основанием прямой призмы является равнобедренная трапеция АВСД, в которой АВ=СД= 13 см, ВС = 11 см. АД= 21 см. Площадь диагонального сечения призмы 180 см2 . Найти площадь боковой поверхности призмы. 3. В правильном тетраэдре ДАВС точка Е - середина ребра СД. Найдите угол между прямыми ВС и АЕ. Билет №16 1. Высота правильной четырехугольной пирамиды равна 16 см, а боковое ребро пирамиды равно 20 см. Найдите площадь боковой поверхности пирамиды. 2.Дан куб ABCDA1B1C1D1. Диагональ АС1 равна  .Найдите периметр сечения куба плоскостью РТН, где точки Р, Т и Н – середины ребер ВС, ВВ1 и АВ соответственно.Билет №17 1. В правильной треугольной пирамиде сторона основания равна высоте и равна 12 см. Найдите площадь поверхности пирамиды. 2 . Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь полной и боковой поверхности призмы. Билет №18 1. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой и полной поверхности призмы. 2. В правильной треугольной пирамиде апофема образует с плоскостью основания угол 30º. Сторона основания равна 12 см. Найдите площадь поверхности пирамиды. Билет №19 1.Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы. 2. Через вершину прямого угла К треугольника DKF проведена прямая КМ, перпендикулярная к плоскости этого треугольника. Известно, что КМ = 15 см, FK = DK = 10 см. Найдите расстояние от точки М до прямой DF. Билет №20 1. Прямая МА проходит через вершину квадрата ABCD и не лежит в плоскости квадрата. а) Докажите, что МА и ВС – скрещивающиеся прямые. б) Найдите угол между прямыми МА и ВС, если  .2. Дан куб ABCDA1B1C1D1. Точки К, М и Т – середины ребер СС1, В1С1 и С1D1 соответственно. Найдите АС1, если периметр сечения куба плоскостью КМТ равен  см. |