Урок геометрии 7 кл. Задачи на построение
 Скачать 4.24 Mb. Скачать 4.24 Mb.
|
|
Урок геометрии 7 класс Тема «Задачи на построение»   Тема урока «Задачи на построение» Тип урока - урок изучения нового материала, первичное закрепление новых знаний. Цели урока: 1) дать представление о задачах на построение; 2) рассмотреть наиболее простые задачи на построение и научить учащихся решать их. Задачи урока: познакомить учащихся с задачами на построение; сформировать умение решать простые задачи на построение; расширить знания об истории геометрии. воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов при изучении темы; воспитание интереса к истории математики, как науки. развитие навыков самоконтроля; формирование алгоритмического мышления. Оборудование к уроку: Компьютерный класс, с настроенной сетью и программой NetMeeting. План урока: I.Организационный момент (приветствие, проверка готовности к уроку, постановка цели на урок) II. Проверка теоретических знаний учащихся по теме « Окружность» III. Изучение нового материала 3.1. Актуализация опорных знаний 3.2. Основные задачи на построение. Физкультминутка. IV. Оценка знаний учащихся, подведение итогов урока (рефлексия) Ход урока: I. Организационный момент. Тема сегодняшнего урока - «Задачи на построение». Цель урока – рассмотреть наиболее простые задачи на построение, которые решаются только с помощью циркуля и линейки без делений; научиться решать их. II. Проверка теоретических знаний учащихся по теме окружность. Мы с вами изучили тему «Окружность» и сегодня узнаем, как вы усвоили основные понятия по этой теме, а затем с помощью теста проверим ваши знания. Наш урок будет сопровождаться презентацией. А сейчас ответим на следующие вопросы: 1. Какие существуют способы построения окружности ? (Слайд 2) 2. Какую геометрическую фигуру мы называем ОКРУЖНОСТЬЮ? (Слайд 3) 3. Что мы называем радиусом окружности? (Слайд 4) 4. Что мы можем сказать про все радиусы окружности? 5. Что такое хорда? 6. Что мы называем диаметром окружности? 7. Любые две точки окружности делят её на две части. Как называется каждая из этих частей? (Слайд 5) 8. По рисунку Слайда 6 ответьте на вопросы:  Далее ответьте на вопросы теста, который имеется у вас на карточках самоконтроля: 1. Окружностью называется геометрическая фигура, которая а) состоит из точек плоскости, расположенных на данном расстоянии от данной точки плоскости; б) состоит из всех точек плоскости, расположенных на данном расстоянии от данной точки плоскости. 2. Центром окружности является а) точка, от которой одинаково удалены некоторые точки; б) точка, от которой одинаково удалены все точки окружности. 3. Радиусом окружности называется а) отрезок, соединяющий любую точку окружности с центром; б) отрезок, соединяющий любую точку окружности с центром окружности. 4. Хордой окружности называется а) отрезок, соединяющий две любые точки окружности; б) отрезок, соединяющий две любые точки. 5. Диаметром окружности называется а) прямая, проходящая через центр окружности; б) хорда, проходящая через центр окружности. Самостоятельно оцените свои знания, подсчитав количество верных ответов. А помогут вам оценить верность ваших ответов наши сегодняшние гости – мультипликационные герои Шрек и Фиона. Если верных ответов 5- оценка «5», если верных ответов 4 – оценка «4», если верных ответов 3 – оценка «3», меньшее число верных ответов – оценка « 2». III. Изучение нового материала. 3.1. Актуализация опорных знаний. Сегодня на уроке мы познакомимся с геометрическими задачами на построение. Вы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, строили углы, треугольники и другие фигуры. При этом какими вы пользовались чертежными инструментами? (масштабной линейкой, циркулем, транспортиром, чертежным угольником). Оказывается, что многие построения можно выполнить с помощью только циркуля и линейки без масштабных делений. Поэтому в геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений. Что можно делать с их помощью? Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки. С помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку. А сейчас ребята нам расскажут информацию из истории математики (Слайд 16): 1. В 1672 г. Датский математик Георг Мор, а затем в 1797 г. итальянский учёный Лоренцо Маскерони доказали независимо один от другого такое утверждение: 2. всякая задача на построение, разрешимая с помощью циркуля и линейки, разрешима также с помощью одного только циркуля. 3. Эти название построения носят построения Мора - Маскерони. 4. Швейцарский геометр Якоб Штейнер в 1883 г., а несколько раньше французский математик Жан-Виктор Понселе доказали тоже независимо друг от друга такое утверждение: 5. любая задача на построение, разрешимая с помощью циркуля и линейки, может быть разрешена с помощью линейки, если только в плоскости чертежа задана окружность и её центр. 6. Такие построения носят название построения Понселе - Штейнера. Итак, мы использовали линейку с миллиметровыми делениями и транспортир. Но есть такие задачи, в которых бывает оговорено, с помощью каких инструментов нужно построить предлагаемую геометрическую фигуру. 3.2. Основные задачи на построение. На экран проецируются слайды.   Задача 1. С помощью циркуля и линейки без делений на данном луче от его начала отложить отрезок, равный данному. Чертёж на экране.  У  чащиеся предлагают варианты решений. чащиеся предлагают варианты решений.А теперь проверим ваше решение (см. слайд) и выполним в тетради: Вывод: Очень многие построения в геометрии могут быть выполнены с помощью циркуля и линейки без делений. Такие задачи мы будем называть задачами на построение. Физкультминутка. Мы уже решили задачу № 1. Теперь с помощью компьютера рассмотрим решение задачи № 2. Выполняйте соответствующие построения в тетради. 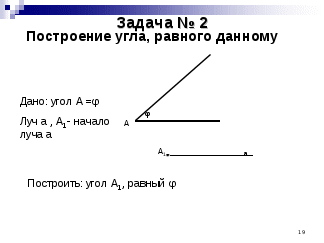    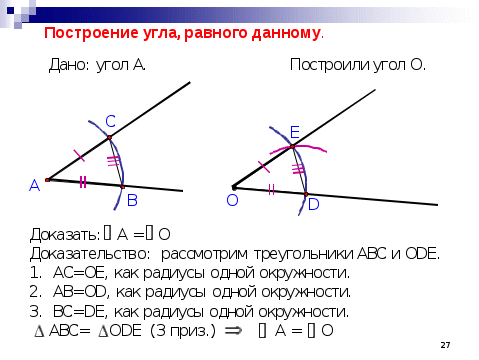  Теперь повторим признаки равенства треугольников (Слайды 24-26) и докажем, что построенный угол равен данному (Слайд 27). Выводы: на сегодняшнем уроке мы познакомились с простейшими задачами на построение с помощью циркуля и линейки. Дома вам предстоит самостоятельно по учебнику разобрать решение двух задач 4 и 5. IV. Подведение итогов урока (рефлексия). Мы изучили много нового, узнали какие задачи можно решить только с помощью циркуля и линейки. У вас у каждого лежит лист с вопросами. Оцените свою работу на сегодняшнем уроке, выбрав один из предложенных вариантов ответа. Собрать листочки для оценки степени усвоения материала сегодняшнего урока, чтобы на следующем уроке правильно организовать работу. Домашнее задание: Геометрия ,7-9:Учеб. для общеобразоват. учреждений Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.-М., 2002. пп. 22-23, В. 17-21 стр.50, задача 5(стр. 45), задача 6 (№153). Сообщаются оценки за урок, включая оценки за тест по теме « Окружность». Приложение 1 Раздаточный материал для учащихся: Ф.И._____________________________ Хорды окружности:___________________________________________________________________ Диаметры окружности:_________________________________________________________________ Радиусы окружности:__________________________________________________________________ 1. Окружностью называется геометрическая фигура, которая а) состоит из точек плоскости, расположенных на данном расстоянии от данной точки плоскости; б) состоит из всех точек плоскости, расположенных на данном расстоянии от данной точки плоскости. 2. Центром окружности является а) точка, от которой одинаково удалены некоторые точки; б) точка, от которой одинаково удалены все точки окружности. 3. Радиусом окружности называется а) отрезок, соединяющий любую точку окружности с центром; б) отрезок, соединяющий любую точку окружности с центром окружности. 4. Хордой окружности называется а) отрезок, соединяющий две любые точки окружности; б) отрезок, соединяющий две любые точки. 5. Диаметром окружности называется а) прямая, проходящая через центр окружности; б) хорда, проходящая через центр окружности. Оцените степень сложности урока. Вам было на уроке: легко; обычно; трудно. Оцените степень вашего усвоения материала: усвоил полностью, могу применить; усвоил полностью, но затрудняюсь в применении; усвоил частично; не усвоил. В начале урока:
В конце урока:
|



