Вопросы и ответы по ПМ. Задачи прикладной механики

Название	Задачи прикладной механики
Дата	26.11.2022
Размер	4.5 Mb.
Формат файла
Имя файла	Вопросы и ответы по ПМ.docx
Тип	Документы #813976

Вопросы по прикладной механике 2 семестр 2021-2022 уч. год

Задачи прикладной механики;

Прикладная механика представляет собой комплексную дисциплину, в которой излагаются основные положения о взаимодействии твердых тел, прочности материалов и методах расчета конструктивных элементов, а также изучает сами механизмы и машины. Она играет большую роль в разработке и создании инновационной техники и оборудования. Любое устройство проектируется на основании тщательных расчетов и методов, которые обязаны отвечать всем принятым стандартам. Исправность работы техники и её долговечность зависят от правильно рассчитанной конструкции, что требует глубоких технических знаний. Учебный курс «Прикладная механика» решает частные задачи, предписанные учебной программой для немашиностроительных специальностей вузов:
1) равновесия материальных тел (статика);
2) рассмотрение основ прочностной надежности элементов конструкций, выбор конструкционных материалов (сопротивление материалов);
3) изучение общих основ построения машин, механизмов и деталей, и приобретение начальных навыков конструирования (детали машин).

Классификация сил, действующих на элементы конструкций. Общие понятия, примеры;
Силы, воспринимаемые элементами конструкции, представляют собой либо объёмные силы, действующие на каждый элемент объёма(собственный вес), либо силы взаимодействия между рассматриваемым элементом и соседними или этим элементом и прилегающей к нему средой(вода, пар, воздух)
Сосредоточенными силами называются давления, передающиеся на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента, например давление колёс подвижного состава на рельсы. Измеряются в единицах силы(тоннах, килограммах, ньютонах)
Распределёнными нагрузками называются силы , приложенные непрерывно на протяжении некоторой длины или площади конструкции. Например : Слой песка одинаковой толщины, насыпанный на тротуар моста, представляет собой нагрузку, равномерно распределённую по некоторой площади; при неодинаковой толщине слоя мы получим неравномерно распределённую сплошную нагрузку. Собственный вес балки какого-либо перекрытия представляет собой нагрузку, распределённую по длине элемента. Распределённые по площади нагрузки выражаются в единицах силы, отнесённых к единице площади (Т/м^2, кГ/см^2, н/м^2 и т. п.). Распределённые по длине элемента – в единицах силы, отнесённых к единице длины (кГ/м, н/м и т. п.)
Постоянные нагрузки действуют во все время существования конструкции, например собственный вес сооружения.
Временные нагрузки действуют на конструкцию лишь в течение некоторого промежутка времени. Примером может служить вес поезда, идущего по мосту.
Статические нагрузки нагружают конструкцию постепенно; будучи приложены к сооружению, они не меняются или меняются незначительно, таково большинство нагрузок в гражданских и гидротехнических сооружениях. При передаче статических нагрузок на конструкцию все её части находятся в равновесии; ускорения элементов конструкции отсутствуют или настолько малы, что ими можно пренебречь.
Если же эти ускорения значительны и изменение скорости элементов машины или другой конструкции происходит за сравнительно небольшой период времени, то мы имеем дело с приложением динамических нагрузок. Их 3 вида
Внезапно приложенные нагрузки передаются на сооружение сразу полной своей величиной. Таковы давления колёс локомотива, входящего на мост.
Ударные нагрузки вознимают при быстром изменении скорости соприкасающихся элементов конструкции, например, при ударе бабы копра о сваю при её забивке.
Повторно-переменные нагрузки действуют на элементы конструкции, повторяясь значительное число раз. Таковы, например, повторные давления пара, попеременно растягивающие и сжимающие шток поршня и шатун паровой машины. Во многих случаях нагрузка представляет собой комбинацию нескольких видов динамических воздействий.
Расчет по группам предельных состояний. I группа расчета. Особенности расчета;
Предельным состоянием называется такое состояние конструкции, при котором она перестает удовлетворять заданным требованиям эксплуатации или изготовления, т.е. дальнейшая эксплуатация конструкции становится невозможной вследствие потери способности сопротивляться внешним нагрузкам или вследствие получения недопустимых перемещений или местных повреждений.

1 группа – по несущей способности. Выполняются расчеты по потере несущей способности или полной непригодности к эксплуатации, т.е. расчеты на прочность, устойчивость, выносливость. Цель расчета: обеспечить прочность конструкции при хрупком, вязком или ином характере разрушения, при потере устойчивости формы конструкции или ее положения, при усталостном разрушении, при разрушении от совместных воздействий силовых факторов и неблагоприятных влияний внешней среды. Расчет по первой группе предельных состояний выполняется в общем случае для всех этапов работы конструкции и ее элементов: изготовления, транспортирования, возведения и эксплуатации.
Расчет по группам предельных состояний. II группа расчета. Особенности расчета;
2 группа – по пригодности к нормальной эксплуатации. Выполняются расчеты на образование, раскрытие (закрытие) трещин и чрезмерные перемещения (прогибы, углы поворота, углы перекоса, амплитуды колебаний). Цель расчета: не допустить в конструкции возникновения чрезмерных перемещений (прогибов, углов перекоса, поворота, колебаний), а также чрезмерного образования и раскрытия трещин, 8 затрудняющих нормальную эксплуатацию или снижающих долговечность конструкции. Расчет по второй группе предельных состояний должен гарантировать сохранение эксплуатационных качеств конструкции с учетом изменчивости прочностных и деформативных свойств материалов.
Расчет по образованию трещин. Трещины в элементе не появляются, если выполняется условие: F ≤ Fcrc , (2.3) здесь F – максимально возможное усилие в сечении элемента от действующей нагрузки; Fcrc – минимально возможное усилие, воспринимаемое сечением перед образованием трещин.
Расчет по раскрытию трещин. Если по условиям эксплуатации образование трещин допустимо, то должна быть ограничена ширина их раскрытия, т.е. должно соблюдаться условие: [ ] acrc ≤ acrc , (2.4) где acrc – установленная расчетами ширина раскрытия трещин; [ ] acrc – установленная нормами предельно допустимая ширина раскрытия трещин, зависящая от условий работы конструкции.
Расчет по деформациям (перемещениям, прогибам). При необходимости ограничения прогиба конструкции должно выполняться условие: 9 f ≤ [ f ], (2.5) где f – установленная расчетами величина прогиба конструкции; [ f ] – предельно допустимое значение прогиба, установленное нормами.
Основные понятия о деформациях и напряжениях;
Как элементы конструкций, так и конструкции в целом при действии внешних сил в большей или меньше степени изменяют свои размеры и форму и в конце концов могут разрушаться. Это изменение носит общее название – деформация.
Величины и характер деформаций связаны со структурой, строением применяемых нами материалов. Все эти материалы могут быть разбиты на два класса : кристаллические и аморфные.
Первые состоят из громадного количества очень малых кристаллических зерен. Каждое из этих зерен представляет собой систему атомов, размещённых на весьма близких расстояниях друг от друга правильными рядами. Эти ряды образуют так называемую кристаллическую решётку. В аморфных материалах мы не имеем правильного расположения атомов. Атомы удерживаются в равновесии силами взаимодействия. Деформация тел происходит за счёт изменения расположения атомов, их сближения или удаления.
Деформации разделяются на упругие и остаточные. Упругими деформациями называются такие изменения формы и размеров элементов, которые исчезают после удаления вызвавших их сил, - тело полностью восстанавливает свою прежнюю форму. Эти деформации связаны лишь с упругими искажениями решётки атомов. Опыт показывает, что упругие деформации наблюдаются, пока величина внешних сил не превзошла известного предела.
Если же внешние силы перешли этот предел, то после их удаления форма и размеры элемента не восстанавливаются в первоначальном виде; оставшиеся разности размеров называются остаточными деформациями.
В элементах конструкции под действием внешних сил возникают дополнительные внутренние силы, сопровождающие деформацию материала. Эти внутренние силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну его часть от другой. Они стремятся восстановить прежнюю форму и размеры деформированной части конструкции.
План решения основной задачи прикладной механики;
Необходимо: 1) Выяснить величину и характер действия всех внешних сил, приложенных к проектируемому элементу, включая и реакции;
2) Выбрать материал, наиболее отвечающий назначению конструкции и характеру действия внешних сил, и установить величину допускаемого напряжения;
3) Задаться размерами поперечного сечения элемента в числовой или алгебраической форме и вычислить величину наибольших действительных напряжений p_max, которые в нём возкинут;
4) Написать условие прочности p_max≤ [p] и, пользуясь им, найти величину поперечных размеров элемента или проверить достаточность уже принятых.
Типы деформаций;
Основными типами деформаций являются: 1) Растяжение и сжатие, пример – работа цепей, канатов, тросов, растянутых и сжатых стержней в фермах, колонн; 2) Перерезывание – работа болтов, заклепок; 3) Кручение – работа валов; 4) Изгиб – работа всякого рода балок. Эти четыре типа деформация называются простыми.
В конструкциях встречается и более сложная работа элементов, когда они испытывают два или более типов деформаций одновременно, например, растяжение или сжатие с изгибом, изгиб с кручением и т.д.; в этих случаях мы имеем дело с так называемой сложной деформацией.
Вычисление напряжений по площадкам, перпендикулярным к оси стержня;
Допускаемые напряжения. Подбор сечений;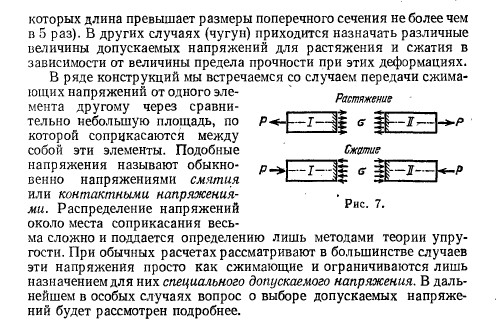
Деформации при растяжении и сжатии. Закон Гука;
Коэффициент поперечной деформации;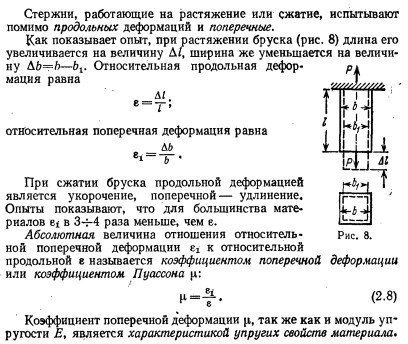
Диаграмма растяжения. Механические характеристики материала;
Диаграмма напряжений;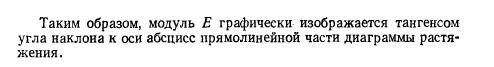
Истинная диаграмма растяжения;
Геометрические характеристики элемента конструкций. Статический момент инерции;
Статический момент относительно данной оси – сумма произведений элементарных площадей dA на их расстояние до данной оси, взятая по всей площади сечения А.
Основной геометрической характеристикой поперечного сечения является статический момент инерции. Он необходим из многих соображений – первое, определения центра тяжести поперечного сечения, второе, расположение относительно центра тяжести остальных геометрических характеристик с целью уменьшения реакции на основную часть решения и получения заниженных характеристик, в дальнейшем которые зададут некоторый запас как прочности, так и устойчивости. Статический момент инерции сечения задается следующей формулой: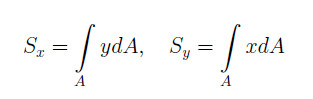
Геометрические характеристики элемента конструкций. Осевой момент инерции площади поперечного сечения;
Момент сопротивления сечения;
Расчет конструкций на прочность. Центральное сжатие;
Центральным сжатием стержня называется деформация его под действием двух равных и прямо противоположных сил, приложенных к концевым сечениям и направленных по оси стержня.
Расчет конструкций на прочность. Прямой плоский изгиб;
Изгиб – это такой вид нагружения, при котором стержень загружен моментами в плоскостях, проходящих через продольную ось стержня.
Плоский изгиб – изгиб, при котором все усилия, изгибающие балку, лежат в одной из плоскостей симметрии балки (в одной из главных плоскостей)
Изгиб называетсяплоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения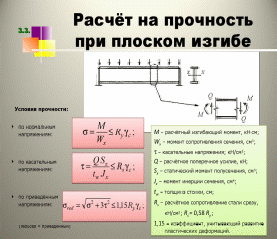
Стадия упругой работы материала. Характерные особенности;
В упругой стадии материал получает преимущественно упругие деформации. Все материалы на этой стадии с тем или иным приближением рассматриваются при расчетах как идеально упругие. Основная зависимость - закон Гука. Эта стадия работы материала является предметом исследования теории упругости.
При упругой деформации тело после снятия нагрузок восстанавливает свои форму и размеры, которые были до деформирования. Упругая деформация связана с изменением расстояний между атомами в пределах параметра кристаллической решетки или параметра ближнего порядка для аморфных тел.
Стадия упругопластической работы материала. Характерные особенности;
Наряду с упругой различают высокоэластическую деформацию, свойственную высокополимерам, которая может достигать сотен процентов. Она возникает под действием нагрузки и исчезает после ее снятия не со скоростью распространения упругой волны (скорость звука в материале), а гораздо медленнее. Скорость возникновения и исчезновения высокоэластической деформации сильно зависит от температуры: увеличивается с ее повышением и уменьшается при ее понижении.
Стадия пластической работы материала. Характерные особенности;
Пластической деформацией (ПД) называют такую, которая сохраняется после снятия нагрузок, приводя к остаточным изменениям формы и размеров тела. Она связана со сдвигом микроскопических частей твердого тела (кристаллов, их частей, отдельных атомов и др.) друг относительно друга на расстояния, значительно превышающие межатомные.
После увеличения нагрузки выше некоторого предела наряду с упругими начинают появляться пластические (остаточные) деформации. У одних материалов (например, металлов) пластическая деформация может достигать значительной величины (пластичные материалы), у других же (например, камни), она является весьма малой (хрупкие материалы). У строительных сталей наблюдается так называемое явление текучести - рост пластической деформации при примерно постоянной нагрузке; после текучести наступает период упрочнения, когда для дальнейшего роста пластической деформации требуется увеличенная нагрузка. Закономерности поведения материала на этой стадии рассматриваются в теории пластичности. Если упругая деформация (при однократном нагружении) практически не влияет на механические свойства материалов, то пластическая деформация приводит к значительному изменению их.
Стадия физически нелинейной работы материала. Характерные особенности;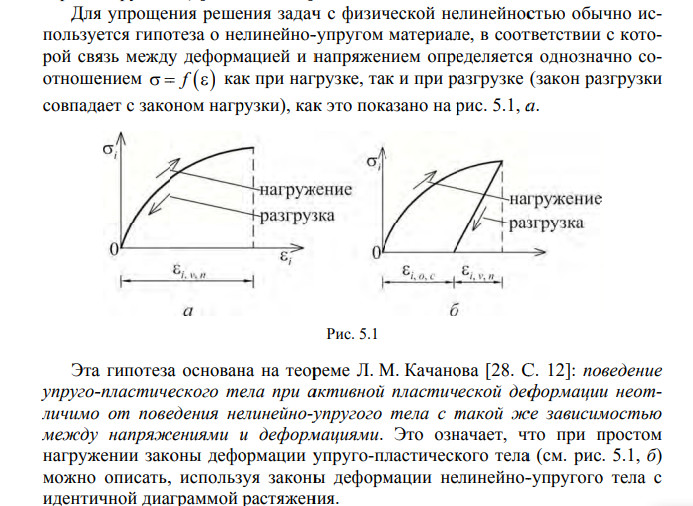
Виды закреплений конструкций. Жесткая заделка. Характерные особенности;
Жесткая заделка ограничивает сразу все возможные степени свободы, дает запрет на перемещение в вертикальном и горизонтальном направлении, а также исключает все возможные повороты. Таким образом, в заделке может возникать как реактивная сила, так и момент. Сила, как правило, раскладывается на вертикальную и горизонтальную составляющие. При этом опорное сечение не может смещаться и поворачиваться.
Жесткая заделка или защемление не допускает ни линейных, ни угловых перемещений опорного сечения. В опоре возникают реакция и реактивный момент. Реакцию также раскладывают на вертикальную и горизонтальную
Виды закреплений конструкций. Шарнирное закрепление. Характерные особенности;
Неподвижная шарнирная опора допускает поворот в любом направлении, поэтому в опоре возникает реакция, проходящая через центр шарнира и имеющая любое направление. Она раскладывается на две составляющих – горизонтальную и вертикальную.
Виды закреплений конструкций. Свободный край. Характерные особенности;
В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном-направлении и поворот опорного сечения.
Подвижная шарнирная опора. Такая опора не препятствует повороту опорного сечения балки и его продольному перемещению, поэтому в ней возникает только одна вертикальная реакция, перпендикулярная плоскости качения и проходящая через шарнира
Статически определимые однопролетные конструкции. Уравнения статики для произвольной плоской системы;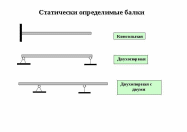
Построение эпюры изгибающего момента при плоском прямом изгибе с применением основных уравнений статики. Характерные особенности в сравнении с методом начальных параметров;
Прямым изгибом называется такой вид простого сопротивления, когда внешние силы приложены перпендикулярно продольной оси бруса (балки) и расположены в одной из главных плоскостей в соответствие с конфигурацией поперечного сечения балки.
При плоском поперечном изгибе в балке возникают два вида внутренних усилий (рис.6.1,в): поперечная сила Q_y , где y – ось симметрии (главная центральная ось) и изгибающий момент M_x. , гдеx – другая главная центральная ось сечения, нормальная к оси симметрии. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.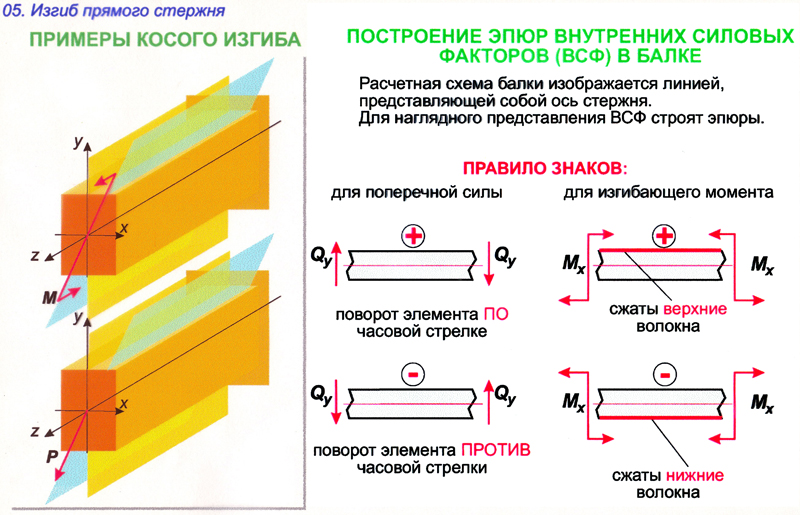
Построение эпюры перерезывающей (поперечной) силы при плоском прямом изгибе с применением основных уравнений статики. Характерные особенности в сравнении с методом начальных параметров;
Метод начальных параметров. Основные понятия. Построение эпюры перемещений при плоском прямом изгибе;
Метод начальных параметров — это способ решения дифференциальных уравнений, при котором неизвестными параметрами являются значение функции и ее производных в начале координат. Для уравнения упругой линии это будут прогиб и угол поворота в начале координат на левом конце балки. Для балки с несколькими участками, для того чтобы произвольные постоянные интегрирования на всех участках были равны, надо, чтобы слагаемые уравнения изгибающих моментов не менялись при переходе от одного участка к другому.
Метод начальных параметров. Основные понятия. Построение эпюры углов поворота при плоском прямом изгибе;
Линейная жесткость. Область применения. Характерные особенности;
Уравнение упругой линии. Характерные особенности. Влияние на нее граничных условий;
Модуль упругости. Понятие, характеристика.
Коэффициент пропорциональности Е , связывающий - нормальное напряжение и относительное удлинение, называется модулем упругости при растяжении(сжатии) материала. Чем больше эта величина, тем меньше растягивается(сжимается) стержень при прочих равных условиях(длине, площади, силе Р). Таким образом, физически модуль Е характеризует сопротивляемость материала упругой деформации при растяжении(сжатии).