Доклад. Задачи специфической тематики задачи на инварианты, применение раскрасок, теория игр. Доклад. Задачи специфической тематики задачи на инварианты, прим. Задачи специфической тематики задачи на инварианты, применение раскрасок, теория игр
 Скачать 191.69 Kb. Скачать 191.69 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Педагогический институт им. В.Г. Белинского Факультет Кафедра физико-математических и «Информатика и методика» естественных наук обучения информатике и математике Направление подготовки: 44.04.01 Педагогическое образование Магистерская программа: Математическое образование Доклад на тему: «Задачи специфической тематики: задачи на инварианты, применение раскрасок, теория игр.» Выполнил: студент гр. 19ЗФПМм Яганина А.А. Проверил: к.п.н., доцент Марина Елена Владимировна 2021 Задачи на инварианты Олимпиадные задачи на инварианты можно условно разбить на два вида: те, в которых требуется доказать некий инвариант, т. е. он явно определен, и те, в которых инвариант используется при решении и сразу не очевиден. Существует также класс задач, при решении которых используются полуинварианты – значения точной верхней и нижней граней для некоторой величины. Наиболее часто они используются в задачах на доказательство экстремума какой - либо величины. Рассмотрим способ решения задач по методу “Инвариант”. В некоторых задачах по математике дается набор преобразований исходного объекта и спрашивается: можно ли, используя эти преобразования, получить из одного состояния объекта другое? Перебором вариантов часто легко убедиться в правильности ответа “нельзя”, однако обосновать этот ответ бывает трудно. Методом, позволяющим во многих случаях решать доказательную часть таких задач, является метод инвариант. Инвариантом называется нечто, не меняющееся в преобразованиях, например, число, набор чисел, четность какого – либо числа и другое. Если значение инварианта в двух состояниях объекта различно, то одно из них нельзя получить из другого. Придумать инвариант должен ученик, самостоятельно решающий задачу; обычно это вызывает у него затруднения. В качестве инварианта чаще всего рассматриваются четность (нечетность) чисел и остаток от деления. Причем применение четности – одна из наиболее встречающихся идей при решении олимпиадных задач. Задача 1. На вешалке висят 20 платков. 17 девочек по очереди подходят к вешалке и либо снимают, либо вешают платок. Может ли после ухода девочек остаться ровно 10 платков? Решение. После подхода первой девочки количество оставшихся платков либо 19, либо 21 (нечетное количество); после подхода второй девочки – либо 18, либо 20, либо 22 (четное количество); после подхода третьей девочки – либо 17, либо 21, либо 23, либо 19 (нечетное количество). После подхода 17 девочки остается нечетное количество платков. Получается противоречие. Значит, 10 платков остаться не может. Задача 2. В таблице, где имеются 15 чисел (-1), можно производить следующую операцию: одновременно изменить знак двух (не более, не меньше) чисел в таблице. Можно ли, применяя эту операцию конечное число раз, получить таблицу, состоящую из (+ 1)? Решение. Ответ: нельзя. Так как число чисел в таблице нечетно, а после каждой операции число чисел (+ 1) в таблице четно. На языке инвариантов это означает: инвариантом таблицы относительно введенной операции является произведение всех чисел в таблице. В начальный момент это произведение равно (- 1), а нам нужно получить таблицу, инвариант которой равен (+ 1). Задача 3. На доске написаны числа 1, 2, 3, …, 1998. За один ход разрешается стереть любые два числа и вместо них записать их разность. В результате многократного выполнения таких действий на доске окажется записанным одно число. Может ли оно быть нулем? Решение. Не может. Так как вначале на доске 999 нечетных чисел. На каждом шаге их количество не меняется, если среди выбранных чисел не более одного нечетного числа. А если выбранные числа оба нечетны, то количество нечетных чисел уменьшается на два. Таким образом, инвариант преобразования: количество нечетных чисел нечетно. Поэтому в конце должно остаться нечетное число. А нуль – четное число. Применение раскрасок Суть самого метода состоит в следующем. Раскрасив некоторые ключевые элементы, которые фигурируют в задаче в несколько цветов, исследовать, что будет происходить, если выполнить условия задачи. Присваивая объектам различные цвета (метки) можно получить дополнительные количественные характеристики, которые позволят упростить понимание задачи и зачастую приводят к четкому, лаконичному решению. Раскрасок, применяемых при решении задач очень много. Какую выбрать – зависит от конкретной задачи, свойств объектов и творческого подхода школьника. Многие задачи повышенного уровня сложности так или иначе связаны с раскрасками. Для своего проекта я выделил три группы подобных задач, часто встречающихся и по уровню сложности доступных школьникам: Задачи, связанные с обходом заданной фигуры. Задачи на замощение/разрезание. Разные (сюжетные) задачи. В решении задач я выделяю два основных этапа: Определить идеи, которые могут привести к решению. Проанализировать, какие исходные данные изменяются при введении дополнительных меток, и как это влияет на решение. Задачи на обход заданной фигуры Очень популярны задачи на шахматной доске, в которых используются как свойства шахматной раскраски, так и особенности «ходов» шахматных фигур. К свойствам шахматной доски относят общее количество клеток, количество черных и белых клеток в отдельности. В решении задач на обход фигуры используются идеи чередования: если объекты двух видов чередуются, то количество объектов одного вида отличается от количества другого вида не более чем на 1. если процесс (путь) начинается и заканчивается на одном и том же объекте, или начало и конец – объекты разного вида, то количество объектов каждого вида одинаковое, а число шагов – четное. Задача 1. В прямоугольном доме (рис.1) 40 комнат и между каждыми двумя соседними комнатами – дверь. Можно ли пройти из в так, чтобы через каждую комнату проходить ровно один раз? 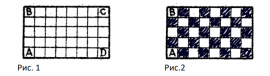 Идеи решения: 1) раскрасим таблицу в шахматном порядке, тогда общее количество клеток можно рассматривать как совокупность белых и черных, 2) при каждом шаге цвет комнаты меняется на противоположный. Решение: Вспомним про чередование: при четном количестве комнат первая и последняя должны быть разного цвета, но это противоречит нашей раскраске (рис.2) Очень популярны задачи с шахматными фигурами. Задача 2. Может ли Карлсон на спор с Малышом обойти шахматным конём всю шахматную доску размером 7 * 7 так, чтобы конь побывал на каждой клетке по одному разу и вернулся в начальную клетку? Решение: Пусть конь стоит на чёрном поле. После очередного хода он окажется на белом поле, т. е. при движении коня цвет поля чередуется. Если конь обойдёт все клетки доски по одному разу, он сделает 48 ходов и окажется на клетке того же цвета, что и клетка, с которой он вышел. С неё на начальную клетку, которая того же цвета, он за оставшийся ход не попадёт. Ответ: не может. Задачи на замощение/разрезание Второй вид задач, часто предлагаемых школьникам – это различные разрезания или замощения. Не существует универсального метода решения подобных задач, и каждый, кто берется за них, может в полной мере проявить свою интуицию, смекалку и творческий подход. Во многих случаях именно раскрашивание дает дополнительные условия, которые помогут найти способ решить задачу или доказать невозможность такого решения. Задача 3. Из доски 8 * 8 вырезали угловую клетку. Можно ли получившийся остаток разрезать на прямоугольники 3 * 1? Решение: Раскрасим клетки доски в диагональном порядке в три цвета. При такой раскраске при любом расположении фигурки 3 * 1 она закрывает по одной клетке разного цвета, значит, если бы мы смогли разрезать прямоугольник на фигурки 3 * 1, то квадратиков каждого цвета было бы равное количество, а у нас цвета 1 – 21 клетка, цвета 2 – 22 клетки. Значит, нельзя разрезать. Ответ: нельзя. Задача 4. Можно ли разрезать квадрат 10 * 10 на прямоугольники 1 * 4? Решение: Раскрасим клетки доски в диагональном порядке в четыре цвета. При такой раскраске при любом расположении фигурки 4 * 1 она закрывает по одной клетке разного цвета, значит, если бы мы смогли разрезать прямоугольник на фигурки 4 * 1, то квадратиков каждого цвета было бы равное количество, а у нас цвета 1 – 25 клетка, цвета 2 – 26 клетки. Значит, нельзя разрезать. Ответ: нельзя. Разные задачи К этой условной группе я отнес задачи, не связанные с обходом фигур или разрезанием/замощением. Это всевозможные задания на построение раскраски по заданным условиям или на раскрашивание фигур, задачи об изменении положения объектов, численные задачи и т.д. Многообразие таких задач очень велико, и ограничивается, пожалуй, только фантазией их составителя. Задача 5. На каждой клетке доски 5*5 сидели бабочки. Вдруг, испугавшись громкого звука, они перелетели на соседние по стороне клетки. Обязательно ли осталась одна клетка свободная? Решение: Раскрасим доску с бабочками в шахматном порядке. Перелетают бабочки на клетку противоположного цвета – с белой на черную и наоборот.  Всего на доске 13 чёрных и 12 белых клеток. Значит, для одной из бабочек, перелетающих с чёрных клеток белой клетки не достанется. А одна чёрная клетка обязательно останется свободной. Ответ: да, останется свободная клетка Задача 6. В клетках квадрата 3*3 расставлены числа. Разрешается к любым двум соседним (по стороне клетки) одновременно прибавлять или отнимать одно и то же число. Можно ли в какой-то момент получить второй квадрат? 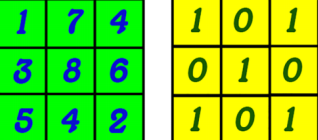 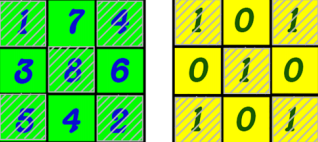 Решение: Заштрихуем клетки каждого квадрата в шахматном порядке В первом квадрате сумма чисел на заштрихованных клетках равна сумме чисел на клетках, которые остались чистыми. Прибавляя (или отнимая) одно и то же число к двум соседним клеткам мы будем изменять одновременно обе суммы. Значит, и в итоговом квадрате равенство сумм должно сохранится, чего не происходит на жёлтой картинке. Получили противоречие. Ответ: нельзя. Теория игр Основные методы решения игровых задач Для решения игровой задачи нужно уметь правильно записать его. И эта запись зависит от того, кто выигрывает в данной игре. Поэтому сначала рассмотрим общие правила записи решения игровых задач. Так как же правильно записать решение игровой задачи? Вообще говоря, это зависит от того, кто выиграет, так как у начинающего есть возможность сделать первый ход, который не зависит от хода соперника. Итак, если выиграет первый, тогда в решении игровой задачи нужно записать: I) его первый ход; II) алгоритм его ходов в ответ на каждый ход соперника, т.е. стратегию победы; III) показать, что у него найдется независимо от хода соперника возможность сделать ход, т.е. его последний ход будет победным. Если же выиграет второй, тогда в решение нужно записать: I) алгоритм его ходов в ответ на каждый ход соперника, т.е. стратегию победы; II) показать, что у него найдется независимо от хода соперника возможность сделать ход. Иногда, бывает нужно записать еще и последний ход, который может не вписываться в общую стратегию. Теперь рассмотрим вопрос о поиске решения задачи. Обычно рассматриваются задачи, в которых один из соперников может предложить выигрышный алгоритм, т.е. обычно предлагаются результативные игры. Идеи стратегий: · Игры, использующие симметрию. · Игры, в которых стратегия — дополнение до фиксированного числа. · Игры, использующие метод выигрышных позиций · Игры-шутки. Игры, использующие симметрию Сейчас мы познакомимся с мощным и красивым, но очень простым методом решения игровых задач - симметричной стратегией. Суть его - делать каждый раз ход, симметричный ходу противника или дополняющий его до чего-либо. Доказательство правильности нашей стратегии будет пользоваться тем, что после каждого нашего хода позиция симметрична: раз так, то если противник сумел сделать свой ход, то и мы сможем сделать ход, симметричный ему. Неправильно думать, что симметрии - стратегия только для второго игрока. Если исходная позиция - несимметрична, то обычно первый игрок может ее как-то сделать симметричной, а потом играть по симметрии, отвечая на ходы второго. Задача 1: Соты имеют форму квадрата 9×9. Все квадратики, кроме центрального, заполнены мёдом. В центре — дёготь. За один ход разрешено разломить соты вдоль любой вертикальной или горизонтальной линии и съесть ту часть, где нет дёгтя. Проигрывает тот, кому остался только дёготь. Кто выиграет при правильной игре? Ответ. Выигрышная стратегия есть у второго игрока. Решение. Для победы второму игроку достаточно совершать ходы, симметричные ходам соперника относительно центра квадрата. Игры, в которых стратегия — дополнение до фиксированного числа Другая идея выигрышной стратегии в играх — дополнение хода соперника до некоторого фиксированного числа, уменьшая каждым «совместным» ходом (т.е. ход первого и второго игрока) общее число элементов на некоторое постоянное число, что сводит игру к игре с меньшим числом элементов, т.е. более простой. Понятно, что победа в данной стратегии зависит от общего количества данных по условию элементов. Задача 2: На столе лежат 15 карандашей. Двое берут по очереди один, два или три карандаша. Проигрывает тот, кому достанется взять последний карандаш. Как должен играть начинающий, чтобы заставить своего противника взять последний карандаш? Решение: Остаток от деления числа 15 на 3 + 1 = 4 равен 3. Начинающему надо, добиться того, чтобы последний карандаш взял противник, поэтому первым ходом он должен взять не 3 карандаша (остаток от деления), а 2 (1 карандаш – противнику!) Затем каждым последующим ходом будет дополнять количество карандашей, взятых вторым игроком, до 4. После первого хода 1 -го игрока на столе останется 13 карандашей, после второго хода — 9, после третьего — 5, после четвертого — 1. Следовательно, последний карандаш берет второй игрок. Метод выигрышных позиций Бесспорно, самый мощный и универсальный способ решения задач на игры - поиск выигрышных позиций. Здесь мы будем называть выигрышной ту позицию, которую выгодно оставлять после своего хода, а проигрышной, соответственно, ту, которую невыгодно. Тогда финальная позиция, из которой уже нельзя сделать ход - выигрышная. Основные свойства позиций таковы: 1.) каждая позиция - либо выигрышная, либо проигрышная (промежуточных вариантов нет!); 2.) из выигрышной позиции можно пойти только на проигрышную; 3.) из любой проигрышной позиции можно пойти на выигрышную. Тогда, если начальная позиция - проигрышная, выигрывает первый, если выигрышная - второй. Стратегия одинакова: каждый раз ходить на выигрышную позицию. Тогда противник должен будет походить на проигрышную позицию (свойство 2), а мы опять сможем пойти на выигрышную (свойство 3). Суть метода: делим всю доску (или все возможные ходы) на два вида полей — выигрывающие и проигрывающие (причем под это определение попадают все рассматриваемые клетки или ходы). После этого стратегия играющего заключается в том, чтобы делать свой ход на выигрывающие клетки (или делать выигрывающие ходы). Данный метод пригоден почти для всех игровых задач. Рассмотрим применение данного метода на конкретной задаче. Задача 3: Имеются две кучки конфет: в одной — 20, в другой — 21. За ход нужно съесть все конфеты в одной из кучек, а вторую разделить на две необязательно равные кучки. Проигрывает тот, кто не может сделать ход. Кто выиграет? Решение: Если мы решили использовать метод выигрышных позиций, то нам нужно найти эти выигрышные позиции. Чтобы их найти, рассмотрим простейшие случаи. Простейшая выигрышная позиция для того игрока, кто ее создал (т.е. «сходил» последним): это 1 и 1. Понятно, что в этом случае побеждает тот, кто ходит вторым, так как у первого игрока нет хода. Очевидно, что позиция 2 и 1 выигрышная для первого и проигрышная для второго. Если 3 и 1, тогда второй вновь с победой, как несложно убедиться простой проверкой, так как есть ровно два хода. Когда в кучках 3 и 2, победа у первого (убираем 3, делим 2). Если же 3 и 3, тогда победа вновь возвращается ко второму, что можно показать простым перебором и т. д. Замечаем закономерность: если в каждой из кучек по нечетному числу конфет, тогда позиция выигрышная для второго. Если же хотя бы в одной из кучек четное число конфет, то такая позиция выигрышная для первого. Несложно понять, что когда в обеих кучках по нечетному числу конфет, то за один ход нельзя получить такую же позицию, так как при разделении любого нечетного числа на два слагаемых одно из них будет четным. Однако если хотя бы в одной из кучек четное (ненулевое) число конфет, то ее несложно разбить на два нечетных слагаемых. Таким образом мы можем разбить все позиции на выигрышные и проигрышные с учетом того, сколько конфет в кучках. И задача выигрывающего делать ход на выигрышные позиции. После этого уже понятно, кто выиграет в данной по условию игре и как ему этого добиться. Делим все возможные ходы на «выигрышные» и «проигрышные». Если после разбиения получились две кучки с нечетным числом конфет, тогда назовем такую позицию «выигрышной», а все остальные — «проигрышные». Стратегия победителя заключается в том, что он делает ход на «выигрышные» поля. Так как первый может сделать ход на «выигрышное» поле, а хода с одного «выигрышного» поля на другое нет, и с любого «проигрышного» поля за один ход можно попасть на «выигрышное», то побеждает начинающий. Своим первым ходом он может съест кучку из 21 конфеты, а кучу с 20 конфетами разделить на две, в которых нечетное количество конфет в обеих кучках (например, 19 и 1). Заметим, что последняя позиция, когда две кучки, по одной конфете в каждой, выигрышная, т.е. последний ход сделает первый. Игры-шутки Самый первый и простой класс игр - игры-шутки, в которых, на самом деле, нет никакой стратегии. Как бы кто ни ходил, либо всегда выиграет первый игрок (тот, кто начинает игру), либо всегда второй. Задача - в том, чтобы математически доказать такую закономерность (а заметить ее можно, сыграв самому с собой раза 3-4). Для доказательства обычно находится какая-то величина, которая понятно, чему равна в начале и конце и понятно, как изменяется на каждом ходу - тут даже частенько число ходов до конца однозначно посчитать можно. Либо какой-то инвариант (т.е. что-то, не меняющееся ни при какой ходе), однозначно зависящий от начальной позиции (чаще всего - от четности) и определяющий выигравшего в конце. Отметим, что часто для нахождения идеи решения задачи можно использовать «метод маленьких чисел», т.е. начинать поиск решения с небольших чисел, который мы уже упоминали в предыдущих разделах. Задача 4: Двое по очереди ломают шоколадку 5x8. За ход можно разломать любой кусок по прямой линии между дольками. Проигрывает тот, кто не может сделать ход (И это такое стандартное условие, что мы его будем подразумевать, если не сказано обратное. Вопрос "кто выиграет при правильной игре?" тоже подразумевается.) Решение: Что значит, что игра закончилась? Конечно, что шоколадка уже вся разломана на отдельные дольки. Долек всегда будет 5x8=40 штук, а шоколадка в начале была одна. Заметим, что на каждом ходу один кусок шоколадки всегда разламывается на 2, т.е. количество различных кусков шоколадки увеличивается на 1. В начале это кол-во было равно 1, а в конце, как мы заметили, 40. Значит, игра продолжалась ровно 39 ходов ("ходом" мы называем ход одного игрока, а не пару "ход - ответный ход"). Поэтому последний (39-й) ход был обязательно ходом первого (его ходы - первый, третий и все с нечетными номерами) - и первый выиграл. |
