задание для самостоятельной работы. Задачи вариантов 1 10, 11 20, 21 30
 Скачать 108.57 Kb. Скачать 108.57 Kb.
|
Задачи вариантов 31 – 40, 41 – 50Применяя закон Ома для участка цепи, законы последовательного и параллельного соединений рассчитать по заданной схеме и значениям сопротивлений резисторов, которым подведено напряжение. Значения R1, R2, R3, R4, U, даны в таблице вариантов (номер варианта – Ваш номер по журналу). Определить ток в цепи, напряжения и токи на всех участках и резисторах цепи. Определить полную мощность цепи и на всех резисторах цепи. При решении задачи обязательно записывать пояснения, формулы, применяемые для расчета, единицы измерения физических величин. 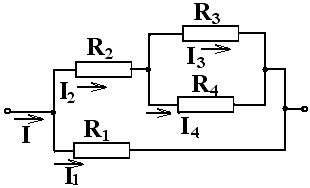 Схема вариантам 31-40. Схема вариантам 31-40. 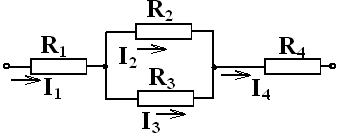 Схема вариантам 41-50 Схема вариантам 41-50Таблица данных вариантам 31-40.
Таблица данных вариантам 41-50
. Примеры решения задач Пример 1 1. Дана электрическая цепь постоянного тока. Необходимо найти эквивалентное сопротивление RЭКВИВ.  Для этого на параллельно соединенных резисторах R3 и R4 найдем их общее сопротивление: их произведение разделим на их сумму: R34 = (R3 ∙ R4) / (R3 + R4) Затем точно также на параллельных участках R6 и R7 найдем их общее сопротивление R67 = (R6 ∙ R7) / (R6 + R7) Резисторы R2 и R34 соединены последовательно, значит, их надо сложить: R2+ R34 = R234 Резисторы R234 и R5 соединены параллельно. Поэтому (как для двух параллельных) их произведение разделим на их сумму: R2345 = (R234 ∙ R5) / (R234 + R5) Получаем, что резистор R1 и эквивалентно рассчитанные участки сопротивлениями R2345 и R67 соединены последовательно, их сложим и найдем полное сопротивление, т. е. эквивалентное сопротивление всей цепи: RЭКВИВ = R1 + R2345 + R67 2. Зная напряжение (или ток), подведенное к цепи, найдем ток (или напряжение) цепи из закона Ома для участка цепи. U = I∙ R или I = U / R 3. Т. к. участки с сопротивлениями R1, R2345 и R67 соединены последовательно, то ток на этих участках одинаков: I1 = I2345 = I67 = I Значит, можем найти напряжение на этих же участках, умножив ток (ток одинаков на последовательных участках цепи!) на сопротивления участков. U1 = I1∙ R1 U2345 = I1∙ R2345 = U234 = U5 , т. к. на параллельных участках цепи напряжение одинаково. U67 = I1∙ R67 = U6 = U7 , т. к. на параллельных участках цепи напряжение одинаково. Зная напряжения на резисторе R5 и участке R234, найдем токи на них: I5 = U5 / R5 ; I234 = U234 / R234 Аналогично (заметьте, напряжение на них одинаково, но сопротивление разное, поэтому и токи разные!): I6 = U6 / R6; I7 = U7 / R7 Проверка: А) должно быть, чтобы сумма токов I6 и I7 равно току I67 на этом участке с сопротивлением R67, согласно первому закону Кирхгофа. I67 = I6 + I7 Б) должно быть, чтобы сумма токов I234 и I5 равно току I2345 на этом участке с сопротивлением R2345, т. е. I2345 = I234 + I5 Но токи на последовательно соединенных участках R2 и R34 цепи одинаковы, т. е. ток I2 равен току на I34, но I34 = I3 + I4 . Запишем это: I2 = I34 = I3 + I4 5. Напряжения на последовательно соединенных участках R2 и R34 цепи равно сумме напряжений U234 = U2 + U34 . Но U34 = U3 = U4 Зная ток I2 на R2, найдем напряжение U2 на нем U2 = I2∙ R2 Также, зная ток I34, найдем напряжение U34 на участке U34 = I34∙ R34 Проверка. Должно быть, что напряжения U34 = U3 = U4 , т. к. напряжение на параллельных участках одинаково. Отсюда найдем из закона Ома токи на резисторах R3 и R4. 6. Остается найти мощности на всей цепи и на отдельных участках по любой из известных формул мощности: Рi = Ii ∙ Ui или Рi = Ii2 ∙ Ri Задача решена в общем виде. Пример 2 Определить эквивалентное сопротивление, напряжение, силу тока на каждом участке электрической цепи напряжением 100В. Сопротивления проводников равны: R1=5,2 Ом, R2=5 Ом, R3=4 Ом, R4=12 Ом, R5=12 Ом. 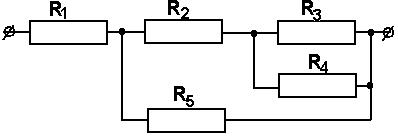 Рис. 1 Решение. Рис. 1 Решение.Первая часть. Резисторы с сопротивлениями R3 и R4 соединены параллельно. Заменим их эквивалентным сопротивлением R34. Тогда получаем:  или R34 = или R34 =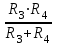 Вычислим: R34 = 3 Ом. Получим эквивалентную схему цепи: 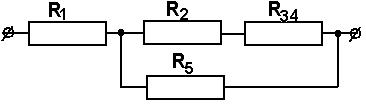 Рис.2 Рис.2Сопротивление последовательно соединенных резисторов R2 и R34 равно их сумме: R234 = R2 + R34. Вычислим: R234 = 5 Ом + 3 Ом = 8 Ом. Эквивалентная схема будет такой: 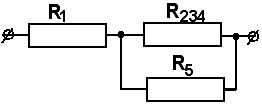 Рис.3 Рис.3Заменим параллельные участки R234 и R5 эквивалентным сопротивлением R234 5 Тогда получаем: 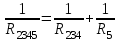 или R2345 = или R2345 =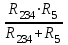 Вычислим: R2 34 5 = 4,8 Ом. Получим эквивалентную схему: Сопротивление последовательно соединенных резисторов R1 и R234 5 равно их сумме: R1234 5 = R1 + R234 5. Вычислим: R12345 = 5,2 Ом + 4,8 Ом = 10 Ом. Эквивалентная схема будет такой: Вторая часть. Перейдем к расчету токов и напряжений. А) Зная полное сопротивление, напряжение цепи можно по закону Ома для участка электрической цепи найдем ток в цепи I= 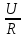 Вычислим: I = 100 В / 10 Ом = 10 А = I1 = I2345 Т. к. резистор R1 и участок сопротивлением R234 5 соединены последовательно, то токи в них одинаковы, и, значит, равны I = I1 = I2345 =10 А. Б) Зная сопротивления на R1 и R2345 и токи, можем найти напряжения исходя из закона Ома U = I •R, т. е. U1 =I ∙R1 и U2345 = I2345 • R2345 Вычислим: U1 = 10 А • 5,2 Ом = 52 В и U234 5 = 10 А • 4,8 Ом = 48 В В) На параллельных участках R234 и R5 напряжения будут одинаковы и равны напряжению U2345 = U5 = U234 = U5 = 48 В. Тогда можем найти ток на последовательно соединенных участках сопротивлениями R2 и R34, где токи одинаковы и равны: I2 = I34 = U234 / R234 Вычислим: I2 = I34 = 48 В / 8 Ом = 6 А. |
