Главная страница
Навигация по странице:

  • 1) расчет показателей анализа рядов динамики ;

  • Изобразить графически эмпирические данные и линию тренда. Сформулировать выводы.

    		•

    ряды динамики. Задание ряды динамики. Задание 1 динамика производства основных продуктов питания в России на душу населения


    Скачать 22.47 Kb.
    НазваниеЗадание 1 динамика производства основных продуктов питания в России на душу населения
    Анкорряды динамики
    Дата14.03.2023
    Размер22.47 Kb.
    Формат файлаdocx
    Имя файлаЗадание ряды динамики.docx
    ТипДокументы
    #989088

    Тема. Ряды динамики
    Задание 1

    Таблица 1. Динамика производства основных продуктов питания в России на душу населения

    Год



    Производство овощей, кг

    1985
    86

    1986
    89

    1987
    87

    1988
    88

    1989
    84

    1990
    77


    Произвести:

    1) расчет показателей анализа рядов динамики;

    2) аналитическое выравнивание по прямой;

    3) рассчитать прогнозное значение анализируемого показателя на год, следующий за последним.
    Изобразить графически эмпирические данные и линию тренда. Сформулировать выводы.


    1. Начальный уровень ряда динамики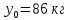



    Конечный уровень ряда динамики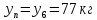

    Средний уровень ряда динамики (средняя хронологическая для интервального ряда)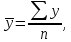

    где ∑y – сумма значений ряда, n – количество уровней ряда.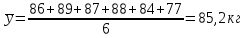

    Абсолютный прирост цепной

    Δi = yi – yi – 1,

    где yi – текущий, yi-1 – предыдущий уровни ряда динамики.
    Абсолютный прирост базисный

    Δi = yi – y1,

    где y1 – начальный уровень ряда динамики.
    Коэффициент роста цепной
    Кр = yi / yi-1,
    Коэффициент роста базисный
    Кр = yi / y1,
    Темп роста цепной
    Тр = yi / yi-1 * 100%
    Темп роста базисный
    Тр = yi / y1 * 100%
    Темп прироста цепной и базисный
    Тпр = Тр – 100%
    Абсолютное значение 1% прироста
    A = 0,01yi-1


    Год
    Пр-во овощей, кг
    Абс. приросты
    Коэф. роста
    Темпы роста
    Темпы прироста
    Абс. знач. 1% прироста

    Баз.
    Цеп.
    Баз.
    Цеп.
    Баз.
    Цеп.
    Баз.
    Цеп.

    1985
    86



























    1986
    89
    3
    3
    1,035
    1,035
    103,5
    103,5
    3,5
    3,5
    0,86

    1987
    87
    1
    -2
    1,012
    0,978
    101,2
    97,8
    1,2
    -2,2
    0,89

    1988
    88
    2
    1
    1,023
    1,011
    102,3
    101,1
    2,3
    1,1
    0,87

    1989
    84
    -2
    -4
    0,977
    0,955
    97,7
    95,5
    -2,3
    -4,5
    0,88

    1990
    77
    -9
    -7
    0,895
    0,917
    89,5
    91,7
    -10,5
    -8,3
    0,84




    1. Уравнение прямой при аналитическом выравнивании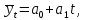



    где 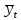– выровненный уровень ряда динамики, a0, a1 – параметры прямо t – условное обозначение времени.

    Система нормальных уравнений для нахождения параметтров по методу наименьших квадратов: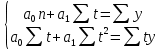



    Примем t = -5; -3; -1; 1; 3; 5, тогда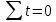



    и система уравнений упрощается.

    Расчетная таблица:

    t
    y
    t2
    ty
    Выровненные значения

    -5
    86
    25
    -430
    89,4

    -3
    89
    9
    -267
    87,7

    -1
    87
    1
    -87
    86,0

    1
    88
    1
    88
    84,3

    3
    84
    9
    252
    82,6

    5
    77
    25
    385
    81,0

    Сумма
    511
    70
    -59
    511





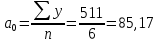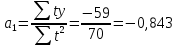    Линия тренда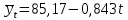



    По этой формуле подсчитаем выровненные значения: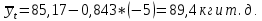



    1. Прогнозное значение на 1991 г. получим, подставив в уравнение t = 7: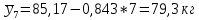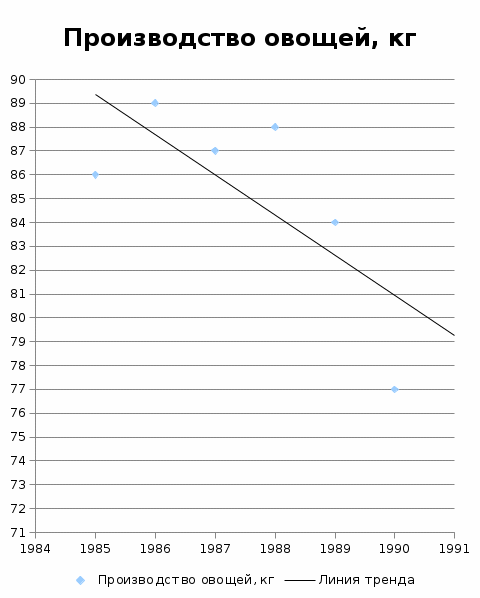





    Выводы. Производство овощей в 1995-1990 г. составляло в среднем 85,2 кг в год. Производство овощей убывало и снизилось за этот период на 9 кг, или на 10,5%.

    написать администратору сайта