Финансовые задачи. Задание 10. Задание 10. Расчет потока платежей
 Скачать 203.5 Kb. Скачать 203.5 Kb.
|
|
Задание 10. Расчет потока платежей. Фирма получила кредит на а) аннуитетными платежами (равные платежи); б) дифференцированными платежами. Выплаты производятся через одинаковые промежутки времени. Исходные данные (вариант 1):
Расчетная таблица
Результаты расчетов оформить в виде таблицы (для каждого случая). В результате сравнения сделать вывод о целесообразности выбора схему выплат для заемщика. а) расчет аннуитетного платежа Аннуитетными, т.е. равновеликими платежами называют платежи, которые производятся на протяжении всего срока кредита равными друг другу. При таком виде платежа заемщик регулярно совершает платеж одного и того же размера. Структура аннуитетного платежа также состоит из двух частей: процентов за пользование кредитом; суммы идущей на погашение кредита. С течением времени соотношение этих величин меняется и проценты постепенно начинают составлять меньшую величину, соответственно сумма на погашение основного долга внутри аннуитетного платежа увеличивается. Поскольку, при аннуитетных платежах в начале сумма, идущая на погашение основного долга, убывает медленно, а проценты всегда начисляются на остаток от этой суммы, то и общий размер уплаченных процентов по такому кредиту больше. Это особенно заметно при досрочных погашениях. В первые периоды кредитования основные выплаты приходятся именно на погашение процентов по кредиту. Величина аннуитетного платежа определяется по формуле: 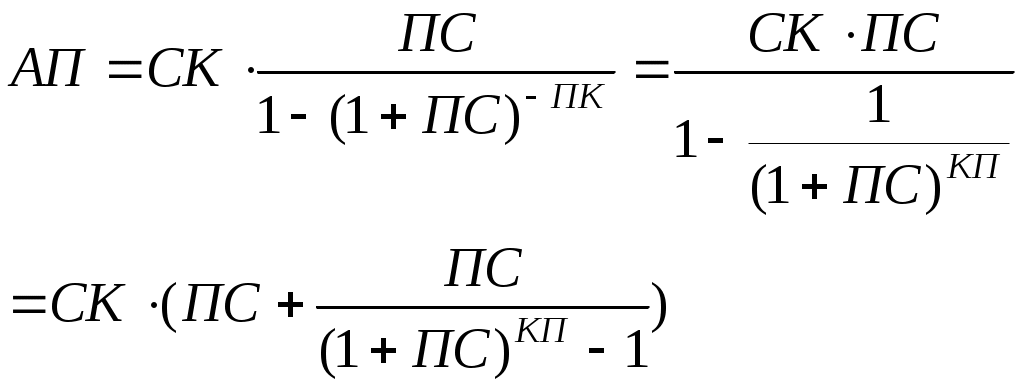 , (1) , (1)где Т.е. если платежи ежемесячные, то Решение: Поскольку срок кредита 2 года, а частота выплат 4 раза в год, тогда количество выплат за весь период составит: Рассчитаем по формуле (1) величину аннуитетного платежа: 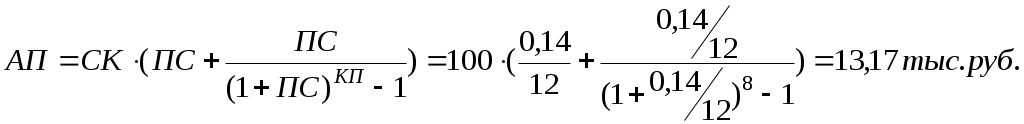 Заносим эту величину в 5 столбец в табл. 1. Проценты по кредиту расчитываются по формуле: где Рассчитывает проценты по кредиту для первой выплаты: Для остальных периодов расчет аналогичен, только с условием меняющегося остатка кредита. Найдем величину погашения кредита по формуле: Тогда Теперь можем полностью заполнить данными строку платежей для первого периода оплаты и найти величину остатка кредита на период второй оплаты Таким образом: Для последующих выплат расчеты ведутся по аналогии: На основе величины остатка по кредиту рассчитываются проценты по кредиту (столбец 4. табл.1). Рассчитывается величина погашения кредита по этому же периоду выплат (столбец 3, табл. 1). Определяется остаток кредита для следующей выплаты. Таблица 1 Расчет аннуитетных платежей
б) расчет дифференцированного платежаДифференцированные платежи в начале срока кредитования больше, а затем постепенно уменьшаются, т.е. регулярные платежи по кредиту не равны между собой. Структура дифференцированного платежа состоит из двух частей: фиксированной на весь период суммы, идущей на погашение суммы задолженности; убывающей части - процентов по кредиту, которая рассчитывается от суммы остатка заложенности по кредиту. Из-за постоянного уменьшения суммы долга уменьшается и размер процентных выплат, а с ними и ежемесячный платеж. Для того чтобы вычислить сумму возврата основного долга, необходимо первоначальную сумму кредита разделить на срок кредита (количество периодов): где На этом сходство в подходах банков заканчивается, и начинаются различия. Состоят они в подходах к вычислению суммы причитающихся процентов. Основных подходов два, разница - в используемой временной базе. Часть банков исходят из того, что «в году 12 месяцев», и тогда размер ежемесячных процентных выплат определяется по формуле: где Часть банков исходит из того, что «в году 365 дней» и такой подход называется расчетом точных процентов с точным числом дней ссуды. Размер ежемесячных процентных выплат в данном случае определяется по формуле: где Решение: Вычислим сумму возврата основного долга по формуле (4): Занесем эту величину в третий столбец табл. 2. Для нашего примера при расчете начисленных процентов будем использовать формулу (5) (в году 12 месяцев). Тогда: Теперь определить общую сумму платежа ( Тогда: Заносим эту величину в пятый столбец табл.2. Далее рассчитываем остаток кредита Также заносим эту величину во второй столбец табл. 2. Для последующих выплат расчеты ведутся по аналогии: На основе величины остатка по кредиту рассчитываются проценты по кредиту (столбец 4. табл. 2). Рассчитывается общая сумма платежа (столбец 5, табл. 2). Определяется остаток кредита для следующей выплаты. Таблица 2 Расчет дифференцированного платежа
Вывод:Сравнивая аннуитетную и дифференцированную схемы, вывод о целесообразности выбора той или другой можно сделать на основе величины переплаты. При аннуитетном платеже общая сумма платежа составила для нашей задачи 105,36 тыс. руб., а при дифференцированном – 105,25 тыс. руб. Таким образом, заемщику следует порекомендовать выбрать схему дифференцированного платежа.Подводя итог можно сказать, что вид платежа является одним из основных параметров кредита, однако рассматривать его необходимо в совокупности с другими параметрами.Задача 6.9. Сдаются в длительную аренду на 20 лет некие производственные площади. Договор определяет чистой доход от аренды в ежегодной сумме 6000 у.е. вносимой в конце года в банк под 11 % (сложные проценты). Найти наращенную сумму и современную величину ренты. Пояснения к решению: Наращенная сумма ( Современная величина ренты ( Поток платежей, все члены которого положительные величины, а интервалы времени между двумя последовательными платежами постоянны, называют финансовой рентой. Ниже приводятся формулы для потока с выплатами в конце периода, так называемые ренты постнумерандо. Общая постоянная рента - последовательность Наращенная сумма 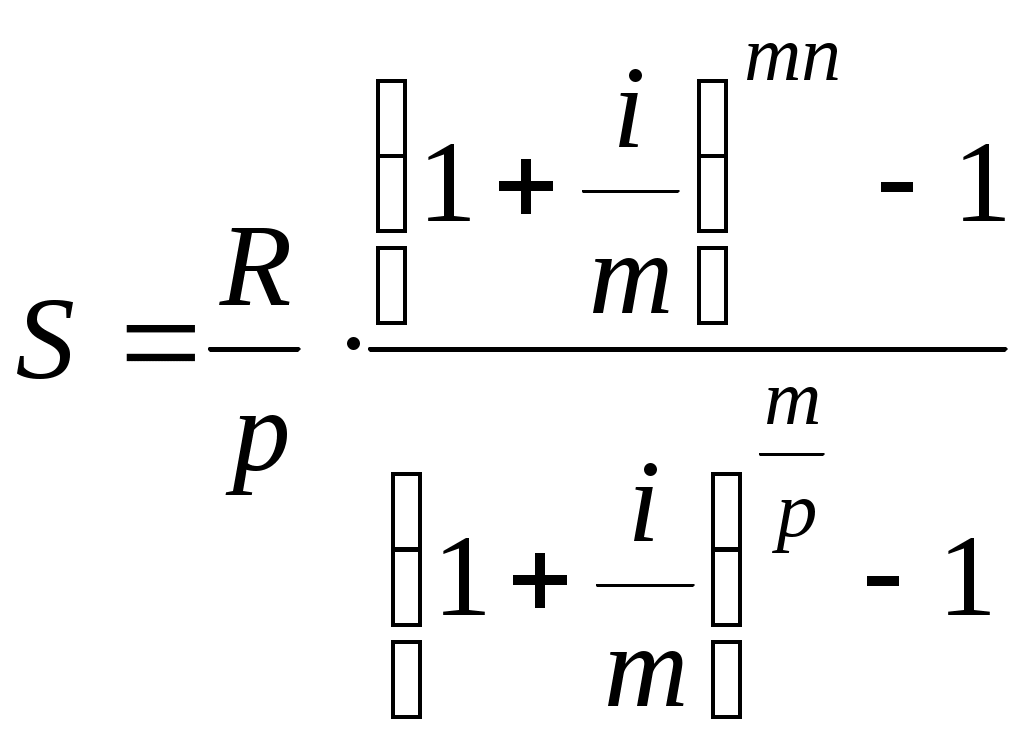 , (8) , (8)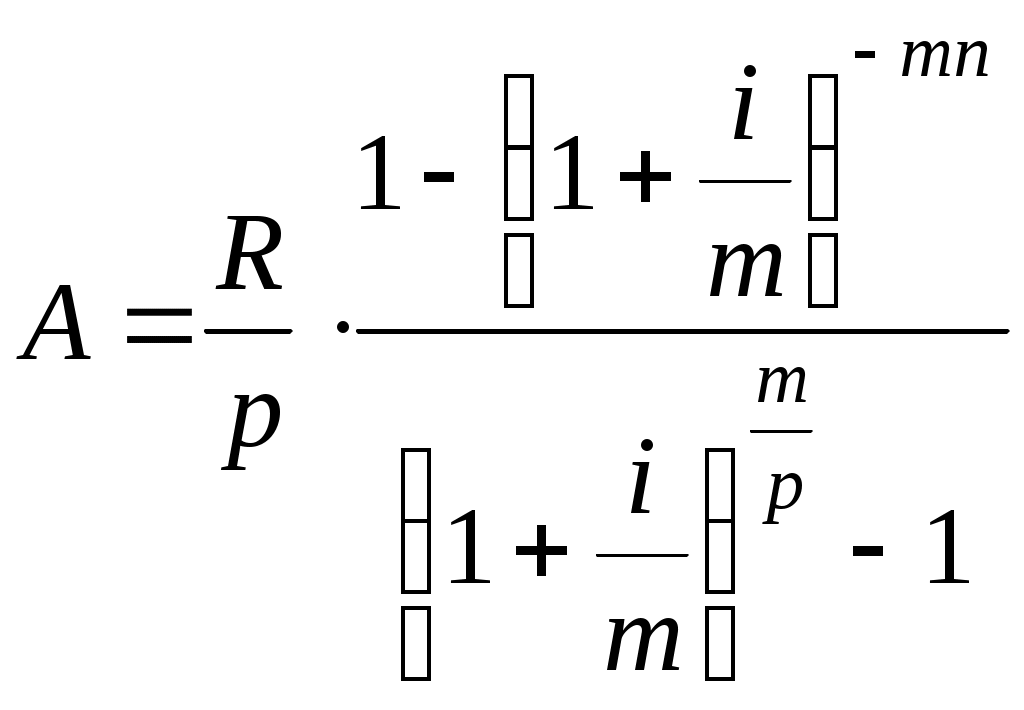 , (9) , (9)где Простая годовая рента - выплаты производятся один раз в конце каждого года, проценты начисляются раз в году ( Тогда, обобщающие характеристики: Решение: Для расчета показателей используем формулы (10) и (11): Задача 6.10. Стоимость пятилетнего обучение в вузе составляет 900000 руб. Плату необходимо вносить равными частями в середине года. Определить сумму, которую надо положить в банк с годовой ставкой 14%, при условии выполнения банком перечисления платы за обучения в вузе. Пояснения к решению: Требуется найти современную стоимость годовой ренты. Для этого используем формулу: Поскольку плату за обучение надо вносить равными частями в середине года, тогда можно рассчитать годовую сумма платежа Решение: Для нашего примера наращенная сумма Таким образом, банк ежегодно будет перечислять за обучение в ВУЗ 180000 руб. Найдем современную стоимость годовой ренты по формуле (12): | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
