ЗАДАНИЕ 2 1в. Задание 2 на курсовую работу по дисциплине Специальные разделы физики Вариант 1 Студент
 Скачать 115.5 Kb.
|
|
ЗАДАНИЕ №2 на курсовую работу по дисциплине «Специальные разделы физики» Вариант 1 Студент _________________________ В пространстве над идеально проводящей плоскостью xOy расположено n точечных зарядов q1, q2, q3,…qn в точках с координатами x1, y1; x2, y2; x3, y3;…xn, yn соответственно. Найти поле скалярного электрического потенциала системы зарядов над плоскостью. Построить эквипотенциальные линии и силовые линии напряжённости электрического поля. Исходные данные для расчёта взять в строке своего варианта в таблице.
Рекомендованная литература
Введение Метод зеркальных изображений При решении ряда технических задач требуется найти электростатическое поле нескольких зарядов в присутствии металлических тел. При этом общее электростатическое поле определяется не только точечными зарядами, но и наведёнными поверхностными зарядами на металлических телах. Задача нахождения поверхностной плотности  наведённых зарядов достаточно сложна. Однако, существует метод, позволяющий для ряда форм металлических тел найти электростатическое поле без нахождения . Суть метода заключается в замене исходной задачи задачей, где металлическое тело удалено, а влияние распределённого по его поверхности заряда учитывается введением фиктивных дополнительных точечных зарядов, величина и положение которых подбираются. Теорема единственности позволяет легко проверить правильность совершённой замены. В рассматриваемой области пространства должны выполняться уравнения электростатики:  и  , а на границе поверхности удалённого металлического тела должны удовлетворяться граничные условия:  и  . Этот метод носит название метод электрических изображений. Рассмотрим его применение для нахождения поля точечного заряда у бесконечной металлической плоскости. Заряд у металлической плоскости Пусть точечный заряд q расположен на высоте h над идеально проводящей плоскостью (рис.1а). 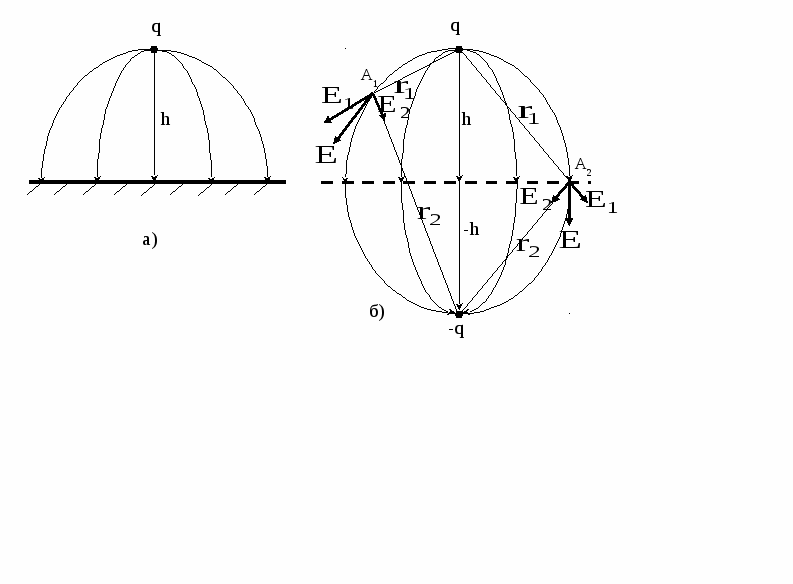 Рис.1. Точечный заряд над металлической плоскостью и его зеркальное изображение Если ввести фиктивный заряд –q, симметрично расположенный относительно плоскости (рис.1б) и убрать из рассмотрения металлическую плоскость, то поле в верхней части такой системы зарядов совпадает с полем системы заряд – плоскость. Действительно, граничные условия на бесконечности и расположение заряда в верхнем полупространстве неизменны, а граничные условия в плоскости симметрии системы двух зарядов совпадают с граничными условиями на металлической плоскости. В любой точке плоскости симметрии вследствие равенства расстояний до зарядов потенциалы, создаваемые зарядами равны по величине и противоположны по знаку. Плоскость симметрии, как и металлическая плоскость, имеет постоянный нулевой потенциал. Поля напряжённостей поля электрических зарядов в плоскости симметрии имеют равные и противоположные по знаку касательные составляющие. Суммарное поле, как и на металлической плоскости, имеет нулевую касательную составляющую. В силу принципа суперпозиции такой поход можно использовать и при большем числе зарядов. Пусть над металлической плоскостью расположено несколько зарядов (рис.2). Для каждого из зарядов введём зеркально отображённый фиктивный заряд и найдём поле скалярного электрического потенциала в такой системе. 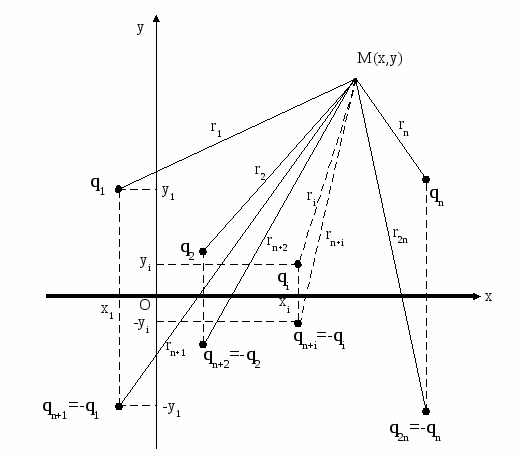 Рис.2. Заряды над плоскостью и их зеркальные изображения Если в исходной задаче мы имели n зарядов, то после введения фиктивных зарядов и изъятия металлической плоскости xOz получаем 2n зарядов. Тогда потенциал в произвольной точке M(x,y)  , (1)где  ,  . (2)С помощью программы POLE-32 осуществим расчёт полей скалярного электрического потенциала и построим эквипотенциальные линии (предполагается, что поля рассчитываются в вакууме). Рассматривается система двух точечных зарядов над металлической плоскостью. Плоскость имеет уравнение y=0, т.е. это плоскость xOz. Значит координаты y зарядов могут быть только положительными. При работе на экране отображается следующее: 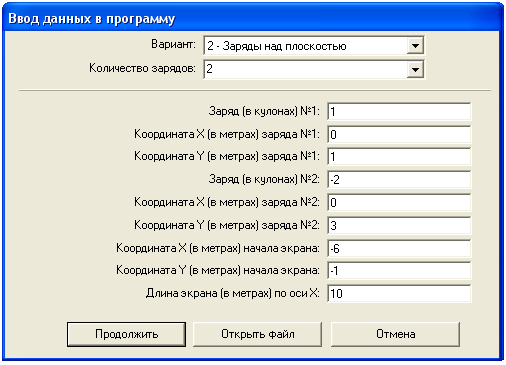 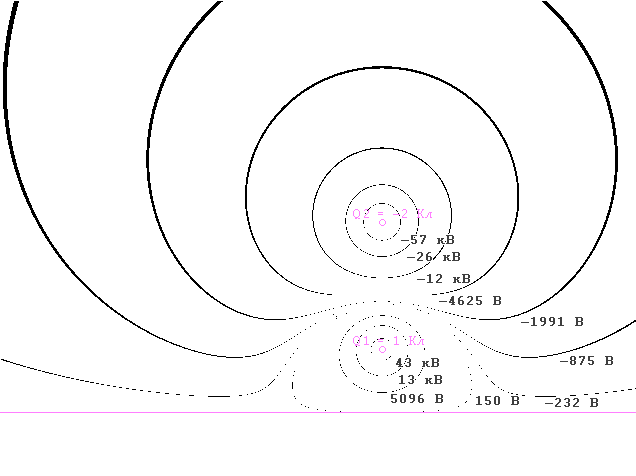 Силовые линии вектора  в каждой точке перпендикулярны линиям равного потенциала и направлены в сторону убывания потенциала.Список литературы
|